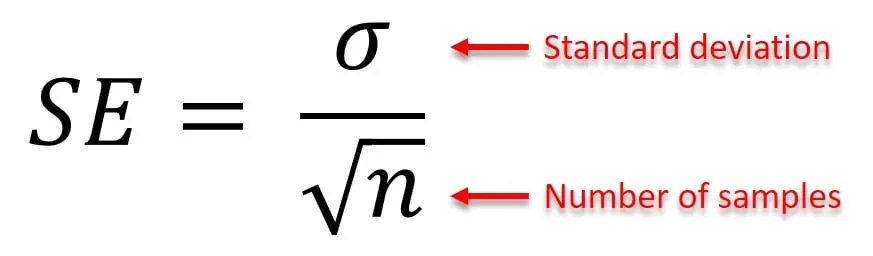
Интересное сегодня
Что такое стандартная ошибка?
Когда вы берете выборки из генеральной совокупности и вычисляете их средние значения, эти средние образуют распределение вокруг истинного среднего значения генеральной совокупности.
Стандартное отклонение этого распределения выборочных средних называется стандартной ошибкой.
Большая и малая стандартная ошибка
Стандартная ошибка показывает, насколько точно среднее значение конкретной выборки отражает истинное среднее генеральной совокупности.
- Большая стандартная ошибка означает, что средние значения разбросаны шире, и ваше выборочное среднее с большей вероятностью неточно отражает истинное среднее генеральной совокупности.
- Малая стандартная ошибка указывает на то, что средние значения расположены ближе друг к другу, и ваше выборочное среднее, скорее всего, является точным представлением истинного среднего.
Стандартная ошибка увеличивается при росте стандартного отклонения и уменьшается с увеличением размера выборки, так как больше данных снижает вариативность результатов.
Формула стандартной ошибки
SE = σ / √n
Где:
- SE — стандартная ошибка выборки,
- σ — стандартное отклонение выборки,
- n — количество элементов в выборке.
Как рассчитать стандартную ошибку
Стандартная ошибка вычисляется путем деления стандартного отклонения выборки на квадратный корень из размера выборки.
- Вычислите среднее значение генеральной совокупности.
- Определите отклонение каждого измерения от среднего.
- Возведите каждое отклонение в квадрат.
- Сложите все квадраты отклонений.
- Разделите сумму квадратов отклонений на (n – 1), где n — размер выборки.
- Извлеките квадратный корень из полученного значения — это стандартное отклонение.
- Разделите стандартное отклонение на √n — это стандартная ошибка.
Вычитая стандартную ошибку из среднего или прибавляя ее к среднему, вы получите диапазон среднее ± 1 стандартная ошибка.
Пример расчета
Допустим, у вас есть выборка значений: 52, 60, 55, 65.
- Вычислите среднее: (52 + 60 + 55 + 65) / 4 = 58.
- Квадраты отклонений: (58 – 52)² = 36, (58 – 60)² = 4, (58 – 55)² = 9, (58 – 65)² = 49.
- Сумма квадратов отклонений: 36 + 4 + 9 + 49 = 98.
- Стандартное отклонение: √(98 / 3) ≈ 5.72.
- Стандартная ошибка: 5.72 / √4 = 2.86.
Часто задаваемые вопросы
1. Что такое стандартная ошибка?
Стандартная ошибка — это статистический показатель, который измеряет точность, с которой выборочное распределение представляет генеральную совокупность, используя стандартное отклонение выборочного среднего.
2. Какая стандартная ошибка считается хорошей?
Определение «хорошей» стандартной ошибки зависит от контекста. Как правило, чем меньше стандартная ошибка, тем лучше, так как это означает, что выборочное среднее надежно оценивает среднее генеральной совокупности. Однако понятие «малой» ошибки может варьироваться в зависимости от масштаба данных.
3. Что показывает стандартная ошибка?
Стандартная ошибка показывает, насколько разбросаны средние значения разных выборок, если бы вы повторяли исследование многократно. Низкая SE означает, что большинство выборочных средних близко к среднему генеральной совокупности, а высокая SE указывает на больший разброс.
4. Когда используется стандартная ошибка?
Стандартная ошибка применяется для оценки неопределенности вокруг среднего значения. Она помогает понять, насколько хорошо выборка представляет всю генеральную совокупность, что важно при построении доверительных интервалов.
5. В чем разница между стандартной ошибкой и стандартным отклонением?
Оба показателя измеряют вариативность, но:
- Стандартное отклонение описывает разброс данных внутри одной выборки.
- Стандартная ошибка показывает, как распределено само среднее значение при многократном повторении выборок.
Формула стандартной ошибки включает стандартное отклонение, деленное на √n.
Литература
- Altman, D. G., & Bland, J. M. (2005). Standard deviations and standard errors. Bmj, 331 (7521), 903.
- Zwillinger, D. (2018). CRC standard mathematical tables and formulas. Chapman and Hall/CRC.
