Модель ожидаемой неожиданности: как динамические ожидания влияют на экономические решения

Введение в модель ожидаемой неожиданности

Теория ожидаемой полезности (Expected Utility Theory, EUT) долгое время считалась основной моделью для анализа принятия решений в условиях риска. Однако за последние десятилетия многочисленные экспериментальные исследования выявили случаи, когда выбор людей не может быть объяснен EUT. Некоторые из этих примеров получили название "парадоксов". В ответ на это были предложены новые теории, такие как теория перспектив (Prospect Theory, PT), расширенная кумулятивная теория перспектив для действий с множественными исходами и теория сожаления.

Несмотря на эти усилия, механизмы принятия решений, объясняющие поведение, не соответствующее EUT, остаются открытой областью исследований. Большинство этих моделей сосредоточены на одноэтапных проблемах, в которых между принятием решения и раскрытием результатов не происходит заметных событий, влияющих на восприятие вероятности исходов. Однако в реальной жизни проблемы принятия решений часто включают сложные процессы, при которых либо структура результатов, либо восприятие людей меняется после принятия решения.

Ограничения существующих моделей

Существующие модели имеют несколько фундаментальных ограничений при работе с многоэтапными проблемами. Теория перспектив и кумулятивная теория перспектив используют нелинейные функции взвешивания вероятностей, однако часто бывает нелегко разделить эффект субъективного восприятия вероятности и оценки результатов. Исследования показали, что форма отображения между объективной и субъективной вероятностью может сильно зависеть от контекста.

Еще одна особенность involves reference point (точка отсчета), которую люди используют для оценки привлекательности результатов. Хотя традиционно используется начальная позиция активов (базовый уровень), recent theories предполагают, что точка отсчета может находиться в других позициях в зависимости от контекстуальных нюансов проблемы и психологических ожиданий людей. По мере усложнения проблем определение "разумной" точки отсчета становится более сложным и субъективным.

Основы модели ожидаемой неожиданности

В данной работе мы предлагаем многоэтапную модель, объясняющую поведение людей при столкновении с проблемами принятия решений, которые involve post-decision information (информация после принятия решения). Основная конструкция модели inspired by важными нейробиологическими открытиями и психологическими теориями.

Во-первых, люди могут как сознательно, так и бессознательно anticipate возможные результаты действия перед его выполнением. Многие модели принятия решений объясняют выбор людей, применяя различные концепции "anticipation" (предвосхищения). Когда животные планируют действие, нейроны в мозге проявляют активность, напоминающую возможные последовательности состояний задачи. Такая последовательная нейронная активность во время процессов anticipation, как сообщалось, predicts последующие принимаемые решения.

Нейробиологические основы модели

Допаминовые нейроны в мозге, которые кодируют reward prediction errors (ошибки предсказания вознаграждения) - отклонение фактического вознаграждения от его ожидаемой value - ответственны не только за обучение, но и за мотивацию действий. Combining эти идеи, мы hypothesize, что сигналы ошибки предсказания вознаграждения, кодируемые во время sequential anticipation состояний задачи, являются essential component в принятии решений.

Более конкретно, мы postulate, что для оценки каждого варианта люди preemptively вычисляют по последовательным stages, насколько ожидаемый результат на текущем этапе отклоняется от ожидаемого результата на предыдущем этапе. Это отклонение затем нелинейно масштабируется "surprise function" (функцией неожиданности), что приводит к тому, что мы называем "anticipated surprise" (ожидаемая неожиданность).

Математический аппарат модели

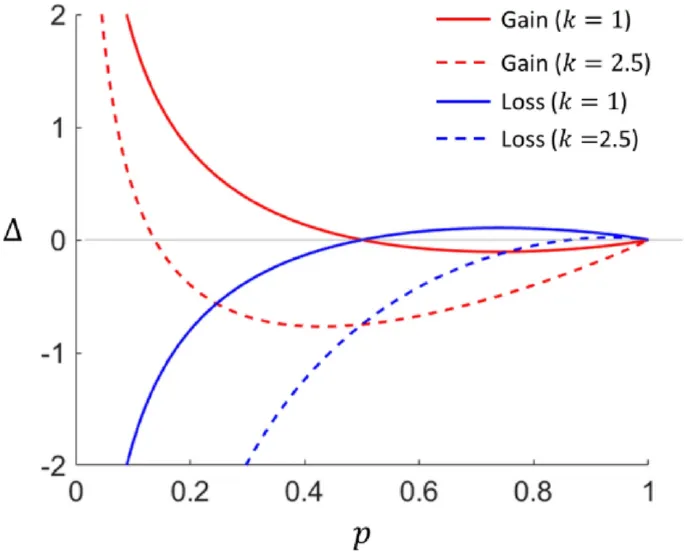
В модели "surprise" (неожиданность) z определяется разностью между "экономо-психологической" ценностью индивидуального денежного исхода в конкретном варианте и expected value всех исходов x в пределах этого варианта: z = x - E(x), где E(.) обозначает expected value.

Значение неожиданности Δ выбора тогда задается формулой: Δ = E(δ(z)), где δ(z) = { f(z) для z ≥ 0; kf(|z|) для z < 0 }.

Здесь f - возрастающая выпуклая функция с f(0) = 0, а k ≥ 1 - фактор aversion to risk (неприятия риска). Выбор формы δ позволяет учесть известные экспериментальные наблюдения, например, risk-averse поведение decision maker при столкновении с 50-50 азартной игрой на равные деньги.

Последовательное предвосхищение в полной модели

Многие модели принятия решений, включая теорию перспектив, предполагают единую, статическую точку отсчета для каждой проблемы. Однако в проблеме с последовательными структурами ожидания людей generally меняются по мере поступления новой информации о результатах, что игнорируется в теории перспектив. Это учитывается в полной модели ожидаемой неожиданности.

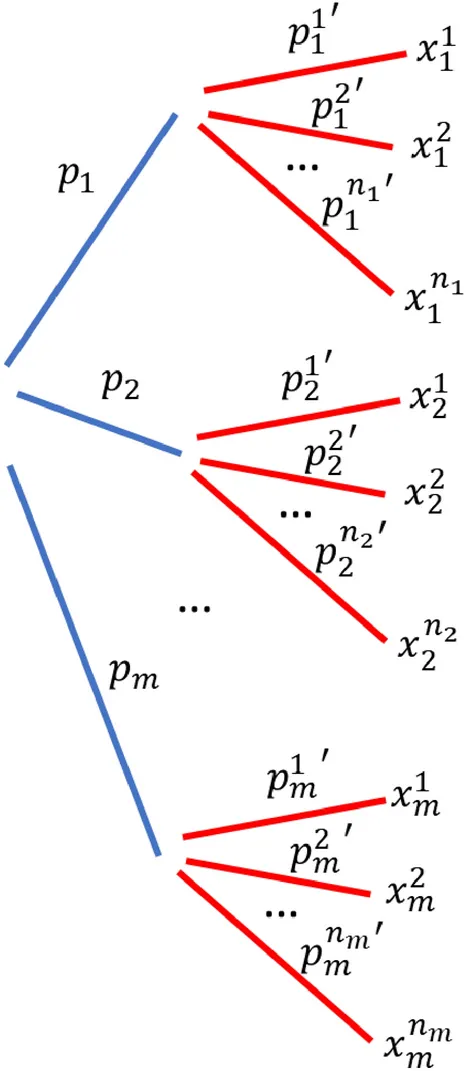
Чтобы построить полную модель из скелетной, мы предполагаем, что люди мысленно симулируют возможные последовательности событий, включающие промежуточные состояния во время процессов принятия решений, и anticipate изменение ожиданий при переходе к этим промежуточным состояниям. Во время этого процесса точка отсчета обновляется от состояния к состоянию на основе expected value возможных результатов, доступных из нового состояния.

Применение модели к азартным играм

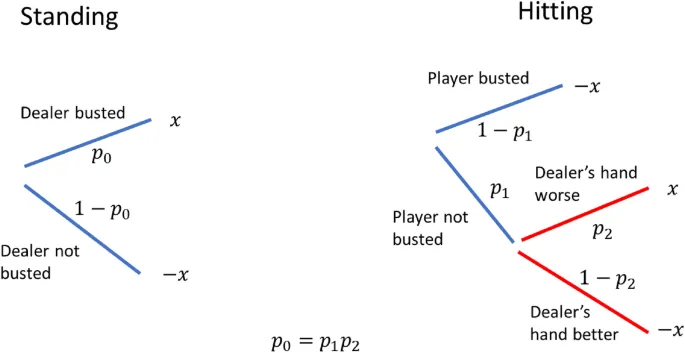
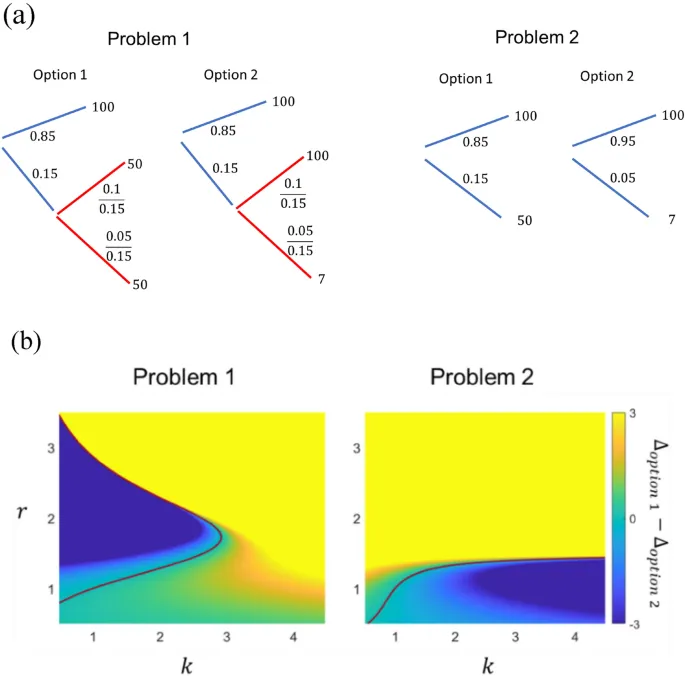
В азартной игре блэкджек есть две фазы игры: фаза игрока и фаза дилера. В начале фазы игрок принимает решение на основе доступной информации о своей руке и руке дилера. В конце фазы игрок может получить новую информацию о своей руке в зависимости от ранее принятого решения. Хотя окончательный результат может все еще быть uncertain, вероятность выигрыша игрока могла измениться, что приведет к обновлению expectation игрока.

Было показано, что expectation информации о результате приводит к изменению gambling behavior и risk preference, а обновление этого expectation также имеет similar effects. Мы проиллюстрируем, как наша полная модель ожидаемой неожиданности capture эффект такого промежуточного состояния и приводит к correct prediction некоторых наблюдаемых gambling behaviors.

Анализ конкретных ситуаций в блэкджеке

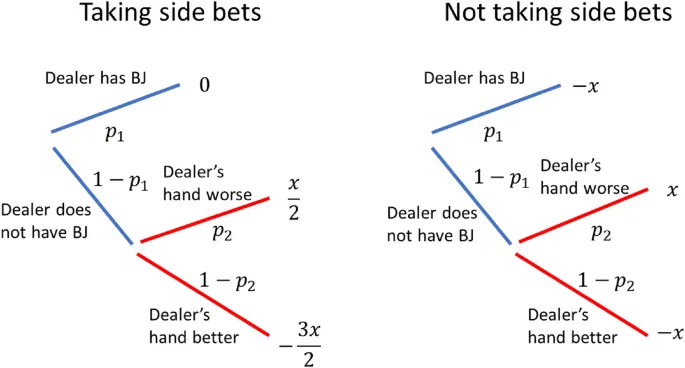
Бennis (2004) outlined 3 scenarios, в которых опытные gamblers сталкиваются с двумя вариантами с очень похожей expected return и подавляюще выбирают slightly worse option. Это: 1. stand вместо hit, когда карты игрока total 16 очков, а дилера - 10 очков (ситуации 16 против 10); 2. принятие insurance side bets, когда у них blackjack; 3. принятие insurance side bets, когда у них "good hands" - комбинации карт, подразумевающие высокую вероятность выигрыша.

Для простоты мы делаем approximation, что expected returns обоих вариантов exactly equivalent во всех scenarios. Без какой-либо формы restructuring проблемы, варианты hit и stand indistinguishable, поскольку для обоих вариантов возможные outcomes equivalent. С дополнительным constraint, что expected return для обоих вариантов одинаков, подразумевается, что вероятность получения этих outcomes также одинакова. Следовательно, preference для stand не может быть predicted conventional models, включая EUT, PT и RT.

Объяснение парадокса Эллсберга

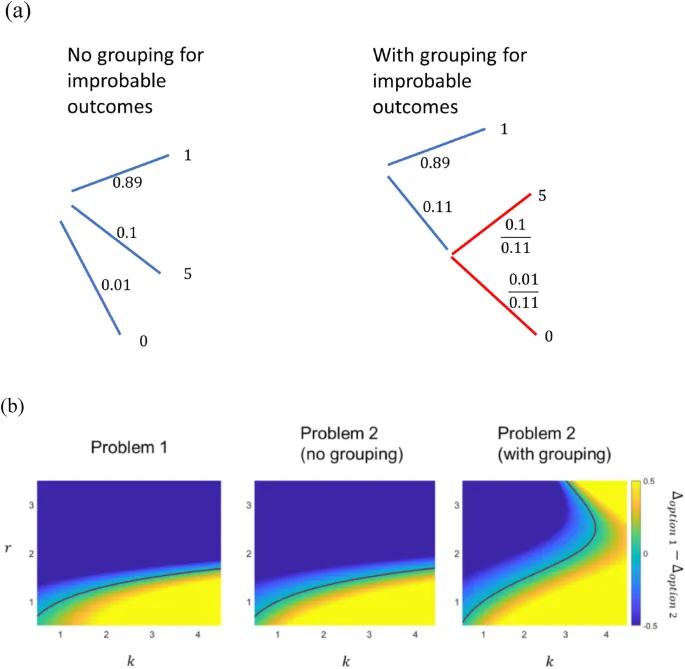
В paradox Эллсберга subjects говорят, что есть две урны: одна содержит n красных шаров и n черных шаров; другая содержит undisclosed количество красных и черных шаров total 2n. Subjects затем выбирают шар в одной из урн. Они выигрывают $1, если шар красный (или черный, цвет не имеет значения в наблюдаемом поведении), и ничего в противном случае. Было показано, что большинство subjects prefer выбирать шары из урны с known ball composition. Это phenomenon известно как ambiguity aversion (неприятие неопределенности).

В контексте нашей модели эти возможные составы урн constitute промежуточные состояния. Промежуточные состояния могут быть parameterized дробью m (m = 0, 1/2n, 2/2n, ..., 1) шаров, которые являются красными. Без дополнительной информации можно assume, что распределение вероятностей, лежащее в основе составов шаров, symmetric about четное количество красных и черных шаров.

Сравнение с другими моделями принятия решений

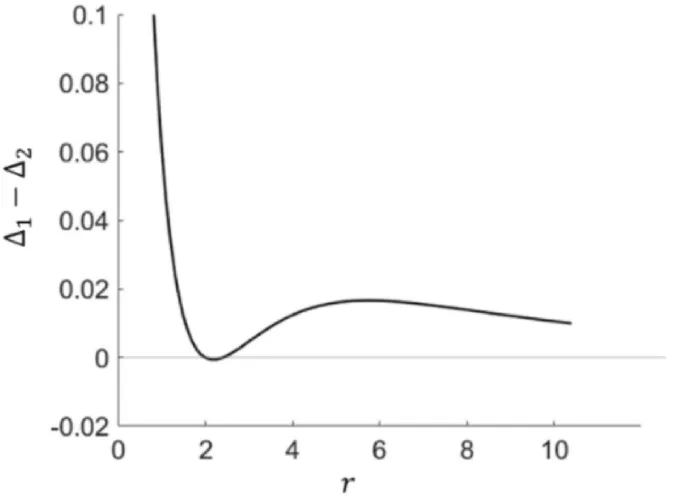
Одно из самых striking differences между теорией перспектив и моделью ожидаемой неожиданности involves механизм для воспроизведения risk preference людей, observed в проблемах 3, 4, 7, 8, 14 в KT1979. Фундаментальная причина, по которой EUT не может воспроизвести observed risk preference в этих проблемах, заключается в том, что при использовании baseline reference point выпуклость (или вогнутость) функции полезности alone может lead only к risk-seeking или risk-averse поведению независимо от p.

Теория перспектив и кумулятивная теория перспектив tackle эту проблему, вводя probability weighting для противодействия эффекту нелинейности в функции полезности. Более конкретно, overweighting малой вероятности essential для воспроизведения risk preference в этом regime. Логика этого solution также applies для моделей, которые неявно вводят effective probability weighting.

Модели с эндогенными точками отсчета

Несколько недавних моделей используют "expectations" в более общем смысле как точки отсчета. Эти expectations могут определяться либо субъективным анализом контекстов проблем, либо объективными мерами, например, одним или несколькими outcomes в проблеме или statistics, derived from них. Хотя мы believe, что психологические процессы, лежащие в основе этих точек отсчета, влияют на выбор людей, как демонстрируют cited works и empirical evidence, другие laboratory и field studies показали, что математически based expected value также highly relevant в принятии решений.

Нейробиологические и психологические связи

Наша модель основана на двух concepts: "surprise" и "anticipation" о reward outcomes. Оба concepts имеют strong neural и psychological bases. В нейробиологии reward prediction error тесно связан с допаминовыми нейронами. Активность допаминовых нейронов кодирует deviation фактического вознаграждения от ожидаемого вознаграждения, что может быть well approximated expected value across всех возможных вознаграждений.

Что касается anticipation, было показано, что shortly before животное выполняет действие, hippocampus place cells exhibit последовательность firing patterns, которая highly predictive последующей последовательности действий. Это suggests, что эти anticipative patterns may be relevant к планированию и решению, какие действия предпринять субъектом.

Психологические основы модели

В психологии есть теории, предполагающие, что ограничения в perception людей и cognitive abilities могли бы объяснить многие features в теории перспектив, а также некоторые другие observed risk preferences интуитивным образом. Многоэтапные проблемы, которые решает наша модель, в значительной степени outside scope теории перспектив, и применение этих существующих теорий для понимания таких проблем не straightforward.

"Surprise" часто считается emotional state. Понятие людей, anticipating их будущие emotional states, вызванные outcomes в событиях, closely related к affective forecasting. Широко thought, что affective forecasting имеет impact на принятие решений, включая случай, когда outcomes uncertain. Интересно, что такое "emotional anticipation" часто exhibits biases. Например, было показано, что люди tend to overestimate интенсивность и продолжительность их emotional response, в particular для loss regime.

Ограничения и будущие направления исследований

Наша работа предложила "anticipated surprise" как одну из (потенциально многих) сущностей, которые влияют на оценку результатов и, следовательно, на принятие решений. Мы не preclude сосуществование других brain systems и mechanisms, которые также responsible за оценку outcomes. Тот факт, что модель ожидаемой неожиданности игнорирует различия в expected value между вариантами, already hints на alternative system, который focus на указанной разнице expected value.

Известно, что люди capable принимать решения, которые heavily based на expected value при попытке suppress их emotions, например, профессиональные игроки в покер. Поэтому разумно speculate, что упомянутый alternative system более rational и analytic по своей природе, contrasting с моделью ожидаемой неожиданности, которая может быть более emotionally based.

Вычислительные аспекты модели

Наша работа не исследует implementation details процесса оценки варианта, то есть как "anticipated surprise" computed в мозге. Некоторые previous works focus на computational aspects принятия решений, которые involve anticipation и forward simulation. Например, decision field theory proposes, что при столкновении с uncertain options, мы мысленно симулируем many instances потенциального течения событий, каждый с slight variations и иногда simplifications в outcome.

Все эти instances contribute к total utility, и решения принимаются, например, с использованием threshold system. Нет apparent reasons, почему similar process cannot быть применен к computation "anticipated surprise", поэтому наша модель и central ideas decision field theory не mutually exclusive.

Заключение и перспективы

В этой работе мы предложили модель принятия решений, которая объясняет поведение людей в многоэтапных проблемах через концепцию "anticipated surprise" (ожидаемой неожиданности). Модель успешно объясняет различные экономические парадоксы и поведение в азартных играх, которые не могут быть адекватно объяснены существующими теориями.

Модель имеет прочные нейробиологические и психологические основания, linking ее с reward prediction error, affective forecasting и другими established concepts в neuroscience и psychology. Будущие исследования должны быть направлены на экспериментальную validation модели, особенно в контексте сложных многоэтапных проблем принятия решений, которые более точно отражают реальные экономические ситуации.