Интересное сегодня
Регуляция эмоций: психологическая дистанция в языке
Представьте, что вы столкнулись с трудной ситуацией: проблемы на работе, напряженные отношения или п...
Миф о креативности левшей: новое исследование опровергает да...
Вековая вера в то, что левши более креативны, была поставлена под сомнение новым метаанализом, охват...
Кросс-культурные различия в привязанности: исследование Ван ...
Кросс-культурные различия в привязанности: исследование Ван Эйзендорна и Кроненберга Мэри Эйнсворт (...
Опасные расстройства пищевого поведения: смертельные риски
Тяжелые формы нарушений пищевого поведения Ряд психических расстройств представляет серьезную угрозу...
Шон «Пафф Дэдди» Комбс осужден за насилие: психология абьюза...
Шон Комбс признан виновным в насилии над бывшей девушкой Музыкальный магнат Шон «Пафф Дэдди» Комбс н...
Как просоциальные эмоции влияют на принятие экономических ре...
Введение Человеческое принятие решений зависит от множества факторов. Нейроэкономические исследовани...
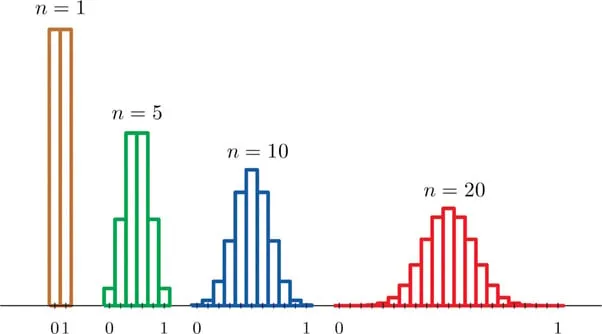
Выборочное распределение в статистике
В статистике выборочное распределение — это распределение вероятностей статистики (например, среднего значения), полученной из всех возможных выборок заданного размера из генеральной совокупности.
Выборочное распределение показывает, как статистика выборки (например, среднее) варьируется при многократном случайном отборе выборок из генеральной совокупности. Оно помогает делать прогнозы о всей совокупности. Для больших выборок центральная предельная теорема гарантирует, что выборочное распределение часто принимает форму нормального распределения.
Цель выборочных распределений
Статистики выборки лишь оценивают параметры генеральной совокупности, такие как среднее значение или стандартное отклонение. Это связано с тем, что в реальных исследованиях из генеральной совокупности отбирается только выборка случаев.
Из-за ограничений по времени и практических сложностей исследователь не может изучить всю совокупность. Поэтому среднее значение выборки, скорее всего, будет отличаться от (неизвестного) среднего значения генеральной совокупности.
Однако исследователь никогда не узнает точную величину ошибки выборки, но с помощью выборочного распределения можно оценить эту ошибку.
Три типа распределений в построении выборочного распределения
- Распределение генеральной совокупности: распределение всех индивидуальных значений или элементов в генеральной совокупности (N).
- Распределения выборок: распределения различных случайных выборок, взятых из генеральной совокупности (n). Хотя концепция «всех возможных выборок» лежит в основе идеи выборочного распределения, на практике мы не выбираем бесконечное количество выборок.
- Выборочное распределение: распределение конкретной статистики (например, среднего), рассчитанной для каждой из возможных выборок.
Как найти выборочное распределение
Важно отметить, что выборочные распределения являются теоретическими, и исследователь не выбирает бесконечное количество выборок.
Шаги построения выборочного распределения
- Начните с генеральной совокупности: В идеале необходимо знать всю генеральную совокупность и её параметры (N). Однако во многих случаях это нецелесообразно или невозможно.
- Выберите размер выборки: Определите размер вашей выборки, обозначаемый как n.
- Отберите случайные выборки: Случайным образом выберите множество выборок размера n из генеральной совокупности. Этот процесс повторяется много раз, каждый раз выбирается новая выборка и вычисляется её среднее значение. Распределение этих выборочных средних и составляет выборочное распределение среднего значения выборки.
- Вычислите статистику выборки: Для каждой выборки рассчитайте нужную статистику (например, среднее).
- Определите разницу: Вычислите разницу между средними значениями выборок для каждой отобранной выборки. Величина разницы может зависеть от размера выборки. Более крупные выборки часто дают более надежные и стабильные оценки среднего значения генеральной совокупности, что приводит к более узкому распределению разниц.
- Постройте распределение: Постройте график разниц в средних значениях выборок, чтобы визуализировать их распределение, и вычислите связанные статистики (например, среднее разниц, стандартная ошибка разницы), чтобы охарактеризовать это распределение.
Центральная предельная теорема
В практических приложениях невозможно отобрать бесконечное количество выборок для создания выборочного распределения. Однако концепция отбора «всех возможных выборок» является теоретической основой идеи выборочного распределения.
На практике свойства выборочного распределения (например, его среднее значение и стандартная ошибка) часто выводятся с использованием статистической теории и данных из одной выборки, опираясь на принципы, такие как центральная предельная теорема.
Центральная предельная теорема утверждает, что независимо от распределения генеральной совокупности, форма выборочного распределения будет приближаться к нормальному распределению по мере увеличения размера выборки (N).
Это полезно, поскольку исследователь никогда не знает, какое среднее значение в выборочном распределении совпадает со средним значением генеральной совокупности. Однако, выбирая множество случайных выборок из генеральной совокупности, средние значения выборок будут группироваться вместе, что позволяет исследователю сделать очень хорошую оценку среднего значения генеральной совокупности.
Таким образом, ошибка выборки уменьшается по мере увеличения размера выборки (n).
Центральная предельная теорема служит основой для многих статистических процедур и выводов, гарантируя, что выборочное распределение среднего значения выборки становится предсказуемым (нормально распределенным) при большом размере выборки.
Дополнительная информация
- Выборочное распределение среднего значения выборки (Kahn Academy)
- Книга «Статистика для психологии» (доступна для скачивания)
