Нормальное распределение (Колоколообразная кривая): Основные понятия и применение

Введение в нормальное распределение (колоколообразная кривая)

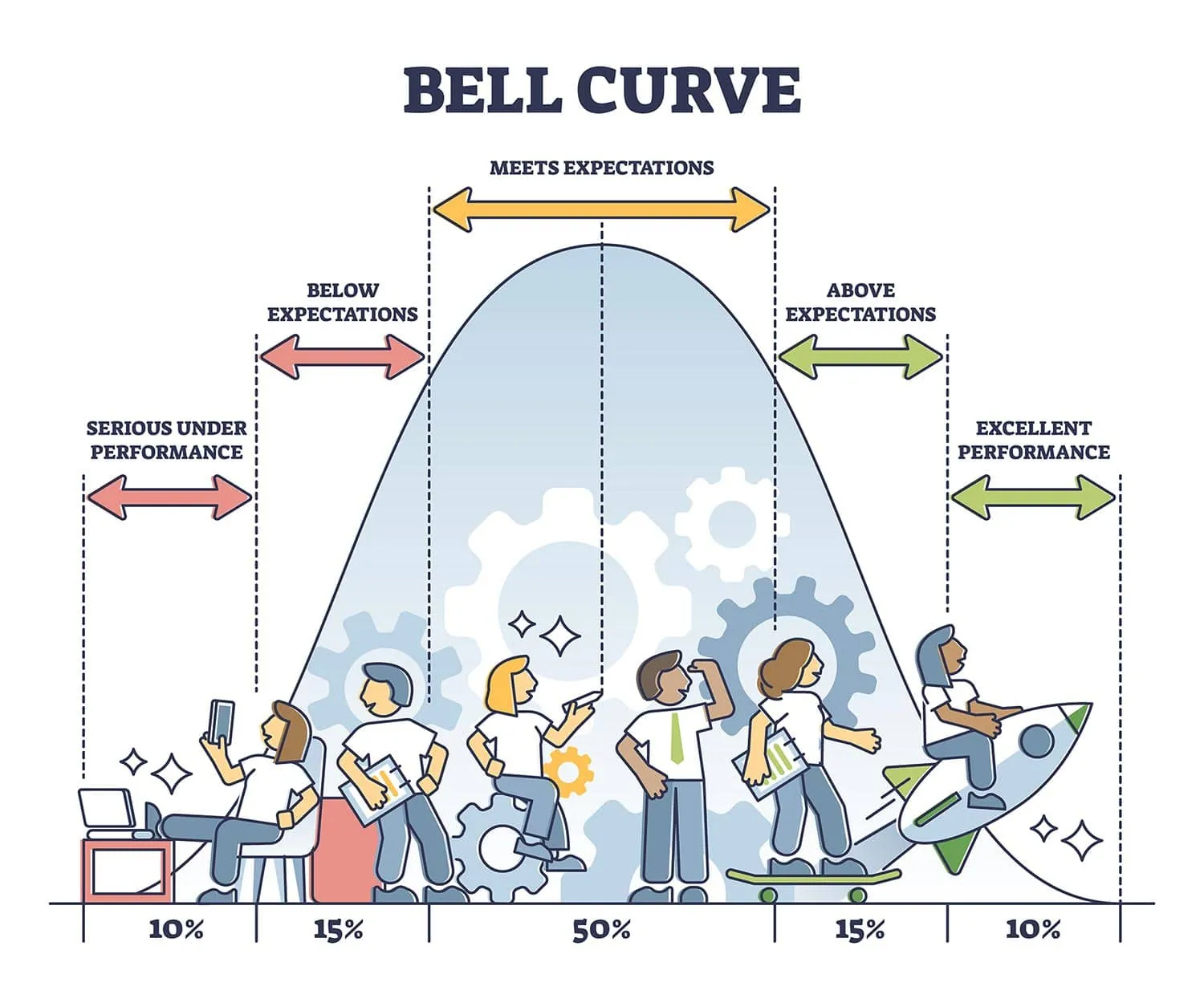
Колоколообразная кривая, также известная как нормальное распределение или распределение Гаусса, представляет собой симметричное распределение вероятностей в статистике. Она изображает график, где данные группируются вокруг среднего значения, с наибольшей частотой в центре и постепенным уменьшением к краям.

Свойства нормального распределения

Нормальное распределение — это непрерывное распределение вероятностей, симметричное относительно среднего значения. Правая сторона центра является зеркальным отражением левой стороны.

• Площадь под кривой нормального распределения представляет вероятность, и общая площадь под кривой равна единице.
• Большинство значений данных в нормальном распределении группируются вокруг среднего, а чем дальше значение от среднего, тем реже оно встречается.
• Хвосты кривой асимптотичны, то есть они приближаются к оси X, но никогда её не пересекают.
• Для идеального нормального распределения среднее значение, медиана и мода совпадают и визуально представлены вершиной кривой.

Нормальное распределение часто называют колоколообразной кривой из-за формы графика плотности вероятности. Оно также известно как распределение Гаусса, в честь немецкого математика Карла Гаусса, который впервые его описал.

Нормальное распределение vs. Стандартное нормальное распределение

Нормальное распределение определяется двумя параметрами: средним значением и дисперсией. Нормальное распределение со средним значением 0 и стандартным отклонением 1 называется стандартным нормальным распределением.

Рисунок 1. Стандартное нормальное распределение (СНР).

Это распределение используется для построения таблиц нормального распределения.

Почему нормальное распределение важно?

Колоколообразная кривая — общая черта природы и психологии

Нормальное распределение — самое важное распределение вероятностей в статистике, потому что многие непрерывные данные в природе и психологии образуют колоколообразную кривую при компиляции и графическом представлении.

Например, если мы случайно выберем 100 человек, мы ожидаем увидеть нормальное распределение для многих непрерывных переменных, таких как IQ, рост, вес и кровяное давление.

Параметрические тесты требуют нормального распределения данных

Самые мощные (параметрические) статистические тесты, используемые психологами, требуют, чтобы данные были нормально распределены.

Если данные не напоминают колоколообразную кривую, исследователи могут использовать менее мощные статистические тесты, называемые непараметрическими.

Преобразование сырых оценок в z-оценки

Мы можем стандартизировать значения нормального распределения (сырые оценки), преобразуя их в z-оценки.

Это позволяет исследователям определить долю значений, которые попадают в определённое количество стандартных отклонений от среднего (например, рассчитать эмпирическое правило).

Что такое формула эмпирического правила?

Эмпирическое правило в статистике позволяет исследователям определить долю значений, которые попадают в определённые расстояния от среднего.

Эмпирическое правило часто называют правилом трёх сигм или правилом 68-95-99.7.

• 68% данных попадают в первое стандартное отклонение от среднего. Это означает, что вероятность случайного выбора оценки между -1 и +1 стандартными отклонениями от среднего составляет 68%.
• 95% значений попадают в два стандартных отклонения от среднего. Это означает вероятность 95%.
• 99.7% данных попадают в три стандартных отклонения от среднего. Это означает вероятность 99.7%.

Как проверить данные на нормальность?

Статистическое программное обеспечение (например, SPSS) может проверить, нормально ли распределены ваши данные, вычислив три меры центральной тенденции.

Если среднее значение, медиана и мода очень близки, данные, скорее всего, следуют колоколообразному распределению.

Также рекомендуется использовать график частот, чтобы визуально оценить форму данных. В SPSS можно добавить кривую распределения к гистограмме: Elements > Show Distribution Curve.

Нормальные распределения становятся более очевидными при более точных измерениях и больших выборках.

Можно также вычислить коэффициенты, которые показывают размер хвостов распределения относительно центра кривой. Например, тесты Колмогорова-Смирнова и Шапиро-Уилка можно рассчитать в SPSS.

Эти тесты сравнивают ваши данные с нормальным распределением и дают p-значение. Если оно значимо (p < 0.05), данные отличаются от нормального распределения (в этом случае мы не хотим значимого результата и нужно p-значение выше 0.05).

Дополнительная информация

• Глубокое определение нормального распределения (Khan Academy)
• Стандартное нормальное распределение и эмпирическое правило (Khan Academy)
• Книга "Статистика для психологии" (скачать)

Эксцесс нормального распределения: 0 или 3?

Нормальное распределение имеет эксцесс, равный 3. Однако иногда используют "избыточный эксцесс", который вычитает 3 из эксцесса распределения для сравнения с нормальным распределением.

В этом случае избыточный эксцесс нормального распределения будет 3 − 3 = 0.

Таким образом, нормальное распределение имеет эксцесс 3, но его избыточный эксцесс равен 0.