Z-оценка: что это и как её использовать в статистике

Z-оценка (стандартный балл)

Z-оценка — это статистический показатель, который описывает положение исходного значения относительно среднего, измеряемого в единицах стандартного отклонения. Положительная Z-оценка означает, что значение выше среднего, а отрицательная — что оно ниже среднего.

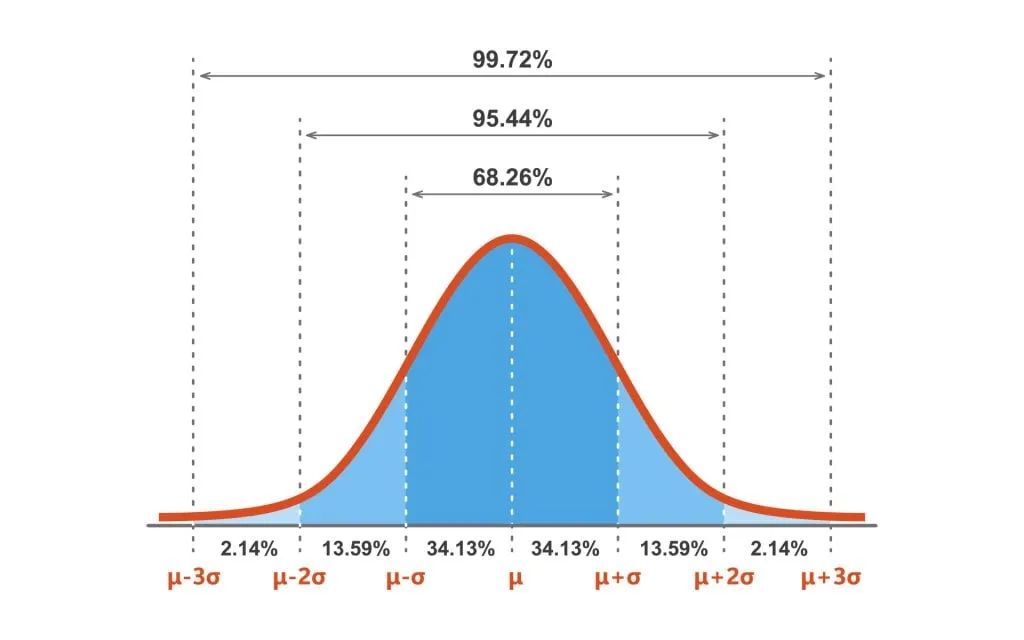
Её также называют стандартным баллом, поскольку она позволяет сравнивать значения разных переменных, стандартизируя распределение. Стандартное нормальное распределение (СНР) — это распределение с формой колокола, где среднее равно 0, а стандартное отклонение (СО) равно 1 (см. рис. 1).

Почему Z-оценки важны?

Стандартизация значений (исходных баллов) нормального распределения путём их преобразования в Z-оценки полезна по следующим причинам:

• Оценка вероятности: Z-оценки помогают оценить вероятность появления определённой точки данных в нормальном распределении. Преобразуя Z-оценки в процентили или используя таблицу стандартного нормального распределения, можно определить вероятность того, что значение окажется выше или ниже заданного порога.
• Проверка гипотез: Z-оценки используются в проверке гипотез для определения значимости результатов. Сравнивая Z-оценку выборочной статистики с критическими значениями, можно принять решение об отклонении или принятии нулевой гипотезы.
• Сравнение наборов данных: Z-оценки позволяют сравнивать точки данных из разных наборов, стандартизируя значения. Это полезно, когда наборы данных имеют разные масштабы или единицы измерения.
• Выявление выбросов: Z-оценки помогают находить выбросы — точки данных, значительно отличающиеся от остальных. Обычно значения с Z-оценками больше 3 или меньше -3 считаются потенциальными выбросами и требуют дополнительного анализа.

Как рассчитать Z-оценку

Формула для расчёта Z-оценки: z = (x – μ) / σ, где:

• x — исходное значение,
• μ — среднее генеральной совокупности,
• σ — стандартное отклонение генеральной совокупности.

Если среднее и стандартное отклонение генеральной совокупности неизвестны, можно использовать выборочное среднее (x̄) и выборочное стандартное отклонение (s) в качестве оценок.

Пошаговый расчёт:

1. Определите исходное значение (x), которое хотите преобразовать.
2. Найдите среднее (μ) набора данных.
3. Вычислите стандартное отклонение (σ).
4. Вычтите среднее из исходного значения (x – μ).
5. Разделите результат на стандартное отклонение ((x – μ) / σ).

Интерпретация Z-оценки

Значение Z-оценки показывает, на сколько стандартных отклонений точка данных удалена от среднего. Чем больше абсолютное значение, тем дальше точка от среднего.

• Положительная Z-оценка: значение выше среднего (например, 1.5 означает +1.5 СО).
• Отрицательная Z-оценка: значение ниже среднего (например, -2 означает -2 СО).
• Нулевая Z-оценка: значение равно среднему.

Другой способ интерпретации — использование стандартного нормального распределения (распределения Z-оценок или вероятностного распределения).

Оценка вероятности

При работе с Z-оценками данные предполагаются соответствующими стандартному нормальному распределению (μ = 0, σ = 1). Это позволяет использовать таблицы или калькуляторы для определения вероятностей.

Эмпирическое правило (правило 68-95-99.7) гласит:

• ~68% данных в пределах ±1 СО (Z-оценки от -1 до 1).
• ~95% данных в пределах ±2 СО (Z-оценки от -2 до 2).
• ~99.7% данных в пределах ±3 СО (Z-оценки от -3 до 3).

Проверка гипотез

Z-оценки используются для определения статистической значимости:

• Односторонний тест: проверяет область слева (левый хвост) или справа (правый хвост) от Z-оценки.
• Двусторонний тест: проверяет оба хвоста распределения.

Уровень значимости (α) — порог для отклонения нулевой гипотезы (обычно 0.01, 0.05, 0.10). Критические значения Z-оценок можно найти в таблицах.

Практические задачи

Примеры:

1. Шкала психологического благополучия (μ = 6, σ = 2). Z-оценка для значения 4? Ответ: (4-6)/2 = -1.
2. Тревожность (μ = 35, σ = 5). Z-оценка для 30? Ответ: (30-35)/5 = -1.

Часто задаваемые вопросы

Можно ли использовать Z-оценки для любых данных?

Они лучше всего подходят для симметричных распределений, но могут дать полезные insights и для других типов данных. Для сильно асимметричных распределений лучше использовать альтернативные методы.

Как Z-оценки улучшают психологические исследования?

Они стандартизируют данные, выявляют выбросы, оценивают вероятность и помогают интерпретировать результаты, повышая точность и объективность исследований.