Надёжность параметров модели Леви в когнитивном моделировании: Психологическая значимость альфа-параметра

Введение в модель Леви и её значение

В соответствии с пятым фундаментальным каузальным вопросом – «Я собираюсь уволиться с работы. Стоит ли мне это делать?» – поставленным Перлом и Маккензи (2018), данная статья исследует аналогичный вопрос в рамках исследований принятия решений: Мы собираемся инвестировать в изучение модели полёта Леви. Стоит ли нам это делать?

Роль вычислительных моделей в когнитивной науке

Когнитивные учёные стремятся понять, как разум обрабатывает информацию для принятия решений, и вычислительные модели играют ключевую роль в раскрытии этих механизмов. Модели последовательного выборки (Sequential Sampling Models, SSMs) особенно эффективны для изучения того, как люди постепенно накапливают доказательства для принятия решения (Рэтклифф и Смит, 2004). Среди SSM модель диффузионного решения (Diffusion Decision Model, DDM) (Рэтклифф, 1978) является наиболее prominentной framework для задач на время реакции с бинарным ответом благодаря своей применимости в различных когнитивных задачах и валидности её параметров в multiple paradigms (Арнольд и др., 2015; Лерче и Фосс, 2017).

Ограничения модели диффузионного решения

DDM предполагает, что принятие решений основано на непрерывном накоплении доказательств, описываемом винеровским диффузионным процессом. В этой модели зашумленная информация накапливается с течением времени из начальной точки (zr) по направлению к одной из двух границ принятия решения (a или 0). Скорость дрейфа (v) указывает на скорость накопления информации, в то время как время принятия решения (ndt) представляет как кодирование стимула, так и выполнение ответа. DDM использует упрощённые предположения из-за ограничений оценки параметров. Однако передовые методы, такие как BayesFlow (Радев и др., 2020), смягчили эти ограничения, проложив путь для разработки более сложных моделей.

Модель полёта Леви: Теоретические основы

Одним из упрощённых предположений в DDM является распределение шума. DDM предполагает, что шум имеет нормальное распределение, что по своей сути содержит предположение о конечной дисперсии. Модель полёта Леви (Lévy Flight Model, LFM) возникает, когда предположение о конечной дисперсии в шуме DDM ослабляется, что приводит к модели, включающей устойчивое распределение.

История и применение полётов Леви

Полёты Леви, популяризированные Мандельбротом (1982), характеризуются случайными блужданиями с тяжелохвостыми распределениями, которые допускают редкие, но значительные скачки. Как обсуждает Нолан (2020), эти модели применялись в различных физических и биологических контекстах, где традиционные гауссовы модели не справляются с объяснением, включая распространение радиоволн в пространстве (Болдырев и Гвинн, 2003; Фриман и Чишам, 2005), поиск пищи животными (Висванатан и др., 1999), перемещение людей (Брокманн и др., 2006) и распространение эпидемий (Бото и Штолленверк, 2009; Брокманн и Хуфнагель, 2007; Линдер и др., 2008; Мачадо и Лопес, 2020).

Применение в когнитивной науке

В когнитивной науке полёты Леви использовались для моделирования аспектов человеческого познания, таких как извлечение памяти (Родс и Тёрви, 2007) и принятие решений (Паттен и др., 2020; Стивен и др., 2009). В то время как эти применения в основном сосредоточены на геометрии самих путей, при моделировании принятия решений человеком интерес должен сместиться с конкретных траекторий на целостные результаты, которые производят эти процессы – specifically, распределение времени реакции (RT) в задачах принятия решений.

Концептуализация модели полёта Леви

Опираясь на эту перспективу, в разделе «Модель полёта Леви и шум» мы представляем нашу концептуализацию модели полёта Леви (LFM), outlining как её теоретические обоснования, так и её особую привлекательность для моделирования времени реакции. Мы также кратко рассматриваем происхождение и развитие модели, particularly в контексте моделей накопления доказательств в принятии решений, как обсуждается далее.

Введение LFM как расширения DDM

Фосс и др. (2019) первыми представили LFM как расширение DDM. Чтобы учесть скачки в процессе принятия решений, они применили LFM в сфере накопления доказательств для моделирования экстремальных событий, similar to обвалы на фондовом рынке (Мантенья, 1991) или смены зон охоты хищников (Висванатан и др., 2008), которые также могут происходить в человеческих решениях. LFM заменяет предположение о гауссовом шуме в DDM на тяжелохвостый шум, позволяя редкие, но экстремальные события, которые проявляются как скачки в процессе принятия решений.

Сравнение качества подгонки моделей

Фосс и др. (2019) продемонстрировали, что, основываясь на AIC (Информационный критерий Акаике), полная LFM – учитывая межиспытательную изменчивость – обеспечивала наилучшее соответствие как в задаче с единичным стимулом, так и в задаче с множественными стимулами (при инструкции, ориентированной на точность). Однако при использовании BIC (Байесовский информационный критерий), который более строго наказывает за сложность, предпочтение отдавалось более простым версиям LFM, particularly для более лёгких задач и условий, ориентированных на скорость.

Параметр стабильности альфа и его интерпретация

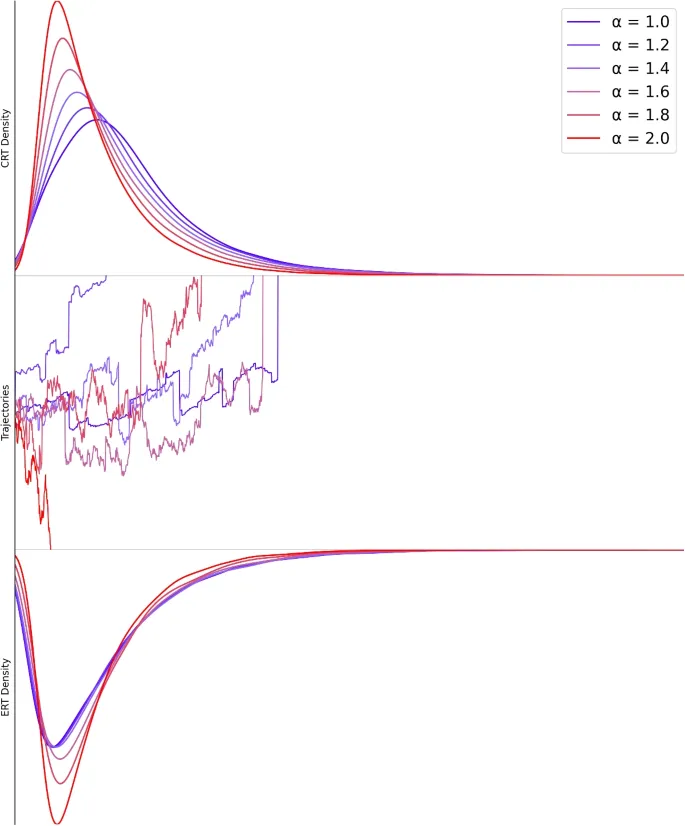
В LFM вероятность экстремальных событий регулируется параметром стабильности lpha , где распределения Гаусса и Коши, характеризующиеся lpha = 2.0 и lpha = 1.0 соответственно, являются special cases устойчивых распределений (см. Рис. 1).

Проблема отсутствия теоретической основы

Значительной проблемой LFM является отсутствие прочной теоретической основы, которая оставляет параметр стабильности (lpha ) без внутреннего meaning, если такая основа не установлена. Эта проблема параллельна проблеме exGaussian распределения, которое, хотя часто используется для обобщения распределений RT, также lacks теоретической интерпретации. Как отмечает Яп и др. (2012), ссылаясь на Мацке и Вагенмейкерс (2009) и Шмидек и др. (2007), параметры exGaussian полезны для capture эмпирических данных, но не должны быть directly linked к когнитивным процессам без теоретического foundation.

Отображение этих параметров на specific когнитивные процессы, как предупреждали Холе (1965) и Макгилл и Гиббон (1965), рискованно без теоретической framework.

Описательная природа параметра альфа

Таким же образом, хотя LFM effectively capture тяжелохвостую природу принятия решений в response к экстремальным событиям, lpha остаётся descriptive параметром без когнитивной интерпретации. Соответственно, соответствие модели provides меру согласованности между данными и предположениями, встроенными в модель. Однако такое соответствие не следует путать с подтверждением ontological точности. Высокое соответствие не обязательно implies, что модель отражает истинный «порождающий процесс», только то, что она capture наблюдаемые patterns в рамках данной formal framework.

Цели и задачи настоящего исследования

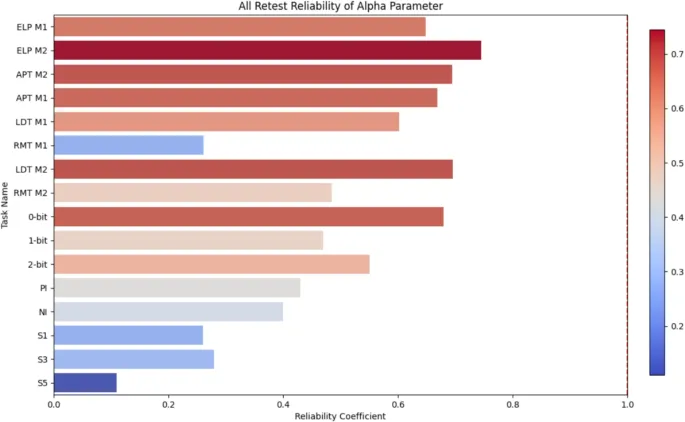
Основная цель данного исследования – устранить это ограничение, изучив потенциальное психологическое significance параметра стабильности (lpha ), подчёркивая, что его надёжность теста-ретеста essential для классификации его как меры когнитивного стиля (Лерче и Фосс, 2017; Шуберт и др., 2016).

Исследование индивидуальных различий

Хотя исследования, изучающие (lpha ), ограничены, Вишен и др. (2020) обнаружили, что сложная LFM produce более низкие значения BIC, чем её аналог diffusion model в обеих задачах в их исследовании, и, что более notably, сообщили о корреляциях в lpha между задачами. Это открытие (наблюдаемая корреляция) вызвало интерес к тому, измеряет ли alpha стабильные межиндивидуальные различия в принятии решений. Они предложили две противоположные гипотезы для объяснения его теоретической основы, aiming направить будущие исследования путем включения других мер когнитивной производительности, таких как интеллект, рабочая память или когнитивная гибкость для testing.

Фокус на надёжности параметра альфа

Нас интересовало, могут ли индивидуальные различия в response к непредсказуемым факторам (в дальнейшем именуемым «скрытые возмущения») отражаться в вариации, capture параметром alpha. Однако вместо direct исследования этих факторов наш «начальный» шаг focused на оценке стабильности самого lpha . Установление надёжности essential, поскольку это гарантирует, что параметр может consistently capture meaningful вариацию. Если lpha отражает trait-like signature в том, как individuals адаптируются к экстремальной дисперсии, его стабильное measurement может открыть новые doors для интерпретации принятия решений beyond моделей central tendency.

Методология исследования

Используя данные из трёх предыдущих исследований с 12 задачами принятия решений (Лерче и Фосс, 2017; Шуберт и др., 2016; Яп и др., 2012), мы провели comprehensive анализ параметров LFM.

Оценка надёжности параметров

Мы assessed коэффициенты надёжности теста-ретеста для оценки стабильности параметров LFM. Кроме того, мы вычислили взаимную информацию (Mutual Information, MI) между параметрами между сессиями, чтобы quantify разделяемую информацию и capture нелинейную надёжность. Дополнительно мы examined корреляции среди параметров LFM для investigation, представляют ли они distinct аспекты данных.

Дополнительные аналитические методы

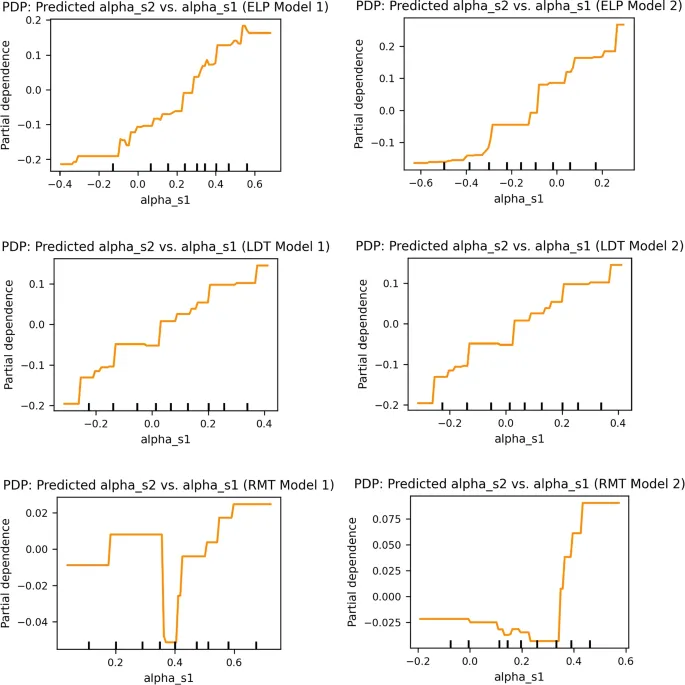
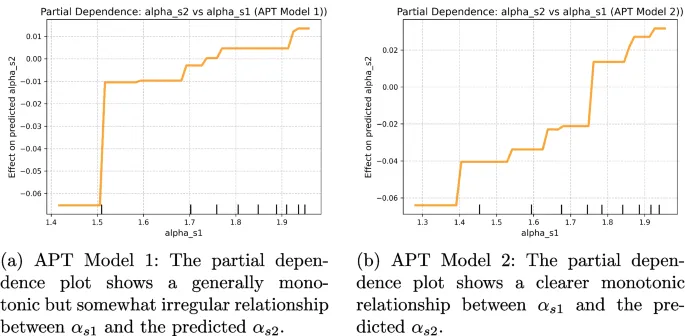
Используя gradient boosting regression (GBR; Фридман (2001); Педрегоса и др. (2011)), мы исследовали intrinsic надёжность параметра alpha. Чтобы further assess часть надёжности, uniquely attributable к alpha, мы employed conditional mutual information (CMI; Cover and Thomas (2006)) analysis. Дополнительно, через regression модели, мы explored specific аспекты данных, capture alpha, такие как его relationship со средним временем реакции ошибок. Кроме того, мы analyzed характеристики predicted распределения времени реакции относительно alpha. Мы также examined влияние практики на обработку информации и производительность.

Ключевые результаты исследования

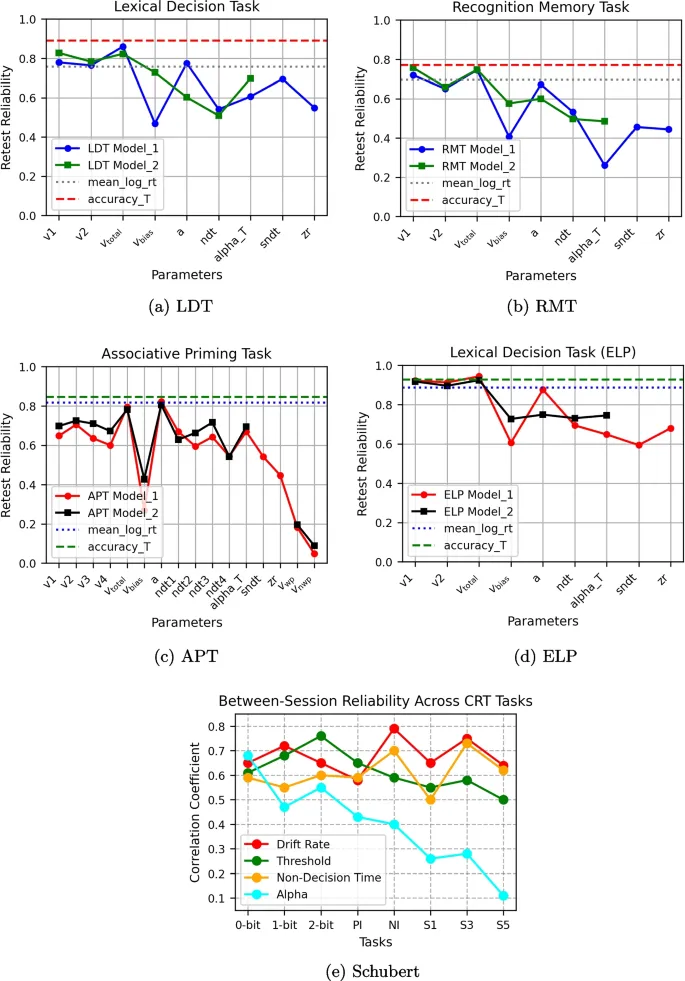
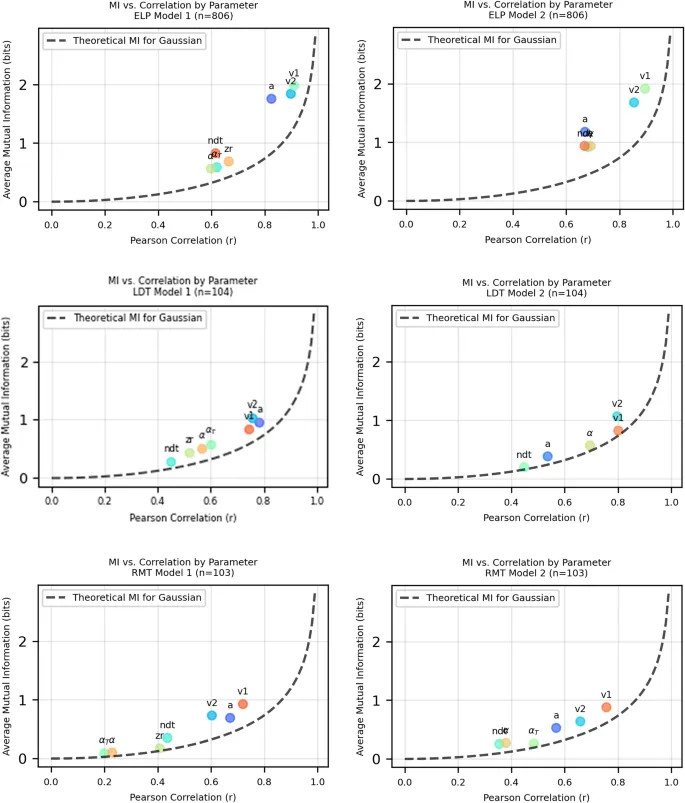
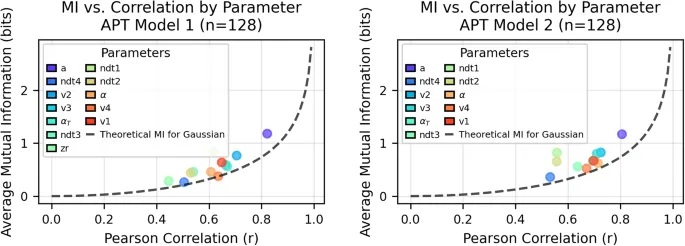
Ключевые findings из нашего исследования confirmed надёжность alpha между двумя сессиями во всех задачах, в то время как significant межзадачная надёжность наблюдалась в более demanding задачах. Сравнения между теоретической MI и plots корреляции revealed, что взаимная информация capture больше разделяемой информации, чем только linear корреляция.

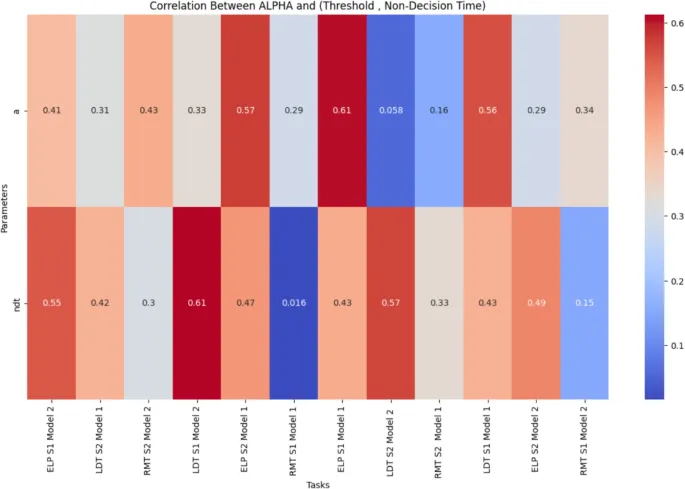
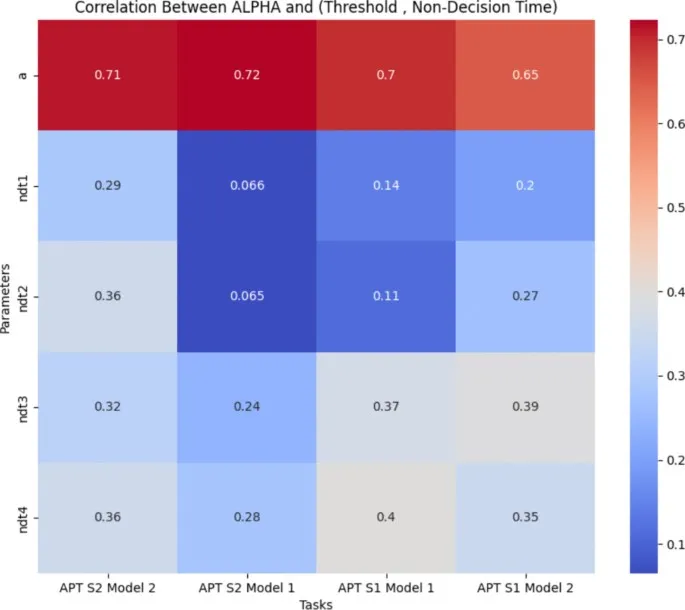
Взаимосвязи между параметрами LFM

Наш анализ interrelations между параметрами LFM revealed, что, хотя большинство параметров showed weak корреляции – underscoring их representation distinct аспектов данных – moderate корреляции наблюдались между alpha, порогом и временем принятия решения. Анализы GBR и CMI confirmed, что надёжность alpha является inherent и не унаследована от других параметров.

Роль альфа-параметра в объяснении ошибок

Мы также found, что alpha имеет strong relationship со средним временем реакции ошибки, indicating его critical роль в объяснении быстрых ошибочных ответов. Дополнительно, наше examination predicted распределения времени реакции found, что lower значения alpha соответствуют shorter времени реакции в initial квартиле как правильных, так и ошибочных ответов.

Влияние практики на когнитивные процессы

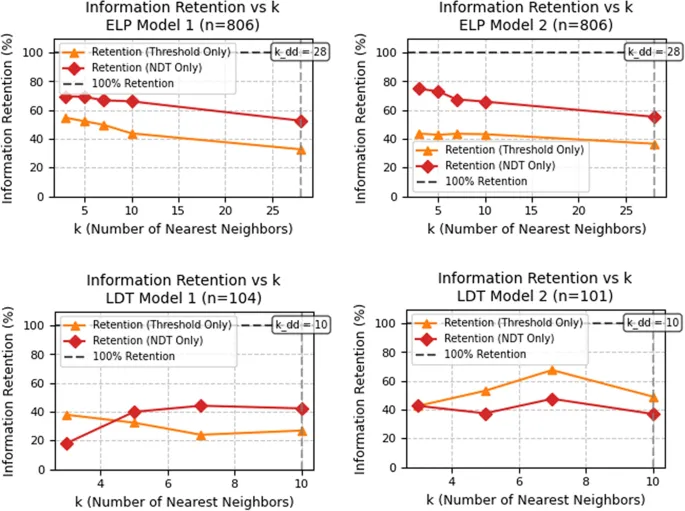
Эффекты практики от первой ко второй сессии improved обработку информации и производительность, как evidenced increased скоростями дрейфа и reduced временем принятия решения и порогами, которые были associated с lower значениями alpha.

Заключение и перспективы будущих исследований

Эти результаты highlight потенциал психологической значимости alpha в capture индивидуальных различий, related к когнитивному функционированию, emphasizing необходимость theoretical framework для full интерпретации этих findings. Будущие исследования should focus на development этой framework и expansion эмпирических исследований для exploration implications alpha в когнитивной обработке across various парадигм принятия решений.

Структура последующих разделов

В следующих разделах мы сначала introduce LFM и роль шума within модели. Subsequently, у нас есть раздел, dedicated к «надёжности», concept, который мы employed для examination, является ли параметр alpha в LFM eligible иметь психологическое significance. Затем мы proceed к описанию данных и report findings, followed обсуждением наших результатов и заключительным разделом.