Интересное сегодня
Введение
Краудсорсинг предполагает использование множества аннотаторов для разметки данных, причем надежность каждого участника обычно неизвестна. Этот метод нашел применение в медицине, физике, инженерии и поведенческих науках. В данной работе исследуется модель дрифф-диффузии — нейронаучно подтвержденный подход к описанию процесса принятия решений — в качестве априорного распределения для поведения аннотаторов.
Модель дрифф-диффузии
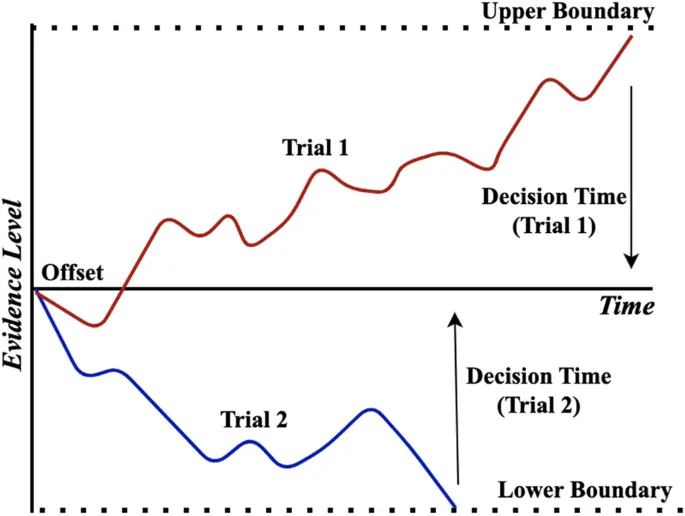
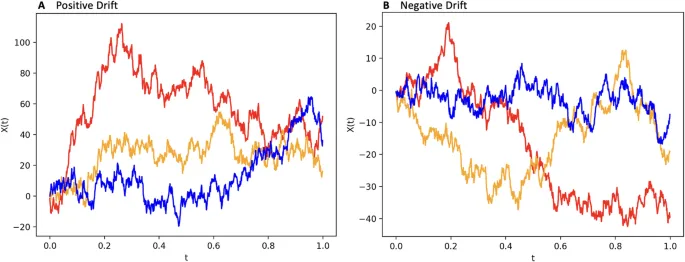
Модель описывает процесс принятия бинарных решений через накопление «уровня доказательности» (evidence level), который изменяется со временем по формуле:
X(t) = μ dt + σ dW(t)
где μ — скорость дрейфа, σ — скорость диффузии, а W(t) — винеровский процесс. Решение принимается при достижении верхней или нижней границы.
Математическая постановка задачи
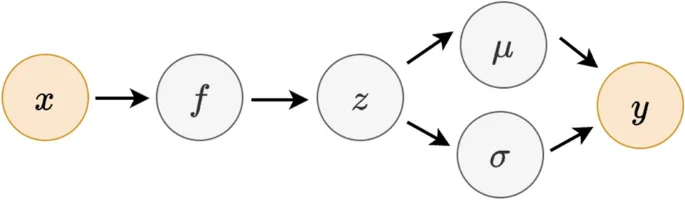
Для входных данных xᵢ ∈ ℝᵐ с неизвестными метками zᵢ ∈ {0,1} аннотаторы присваивают метки yᵢʲ согласно параметрам μ₀ʲ, σ₀ʲ (при z=0) и μ₁ʲ, σ₁ʲ (при z=1). Основные задачи:
- Определение параметров дрифф-диффузии для каждого аннотатора.
- Оценка чувствительности P(yʲ=1|zʲ=1) и специфичности P(yʲ=0|zʲ=0).
- Построение гауссовского классификатора для предсказания меток.
Методы
Вариационный вывод
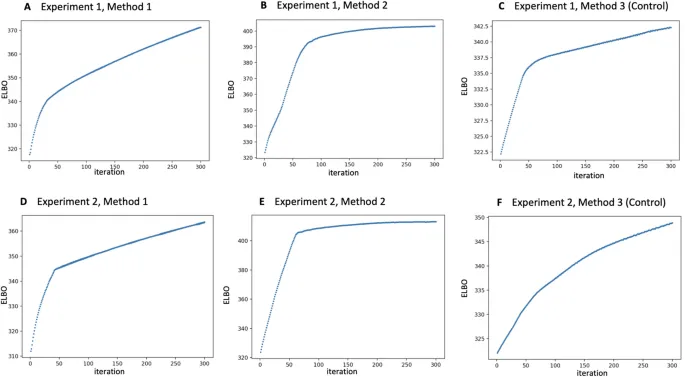
Для максимизации нижней границы доказательности (ELBO) использовано среднее поле:
q(Z,F,μ₀,μ₁,σ₀,σ₁) = q(Z)q(F)q(μ₀,μ₁)q(σ₀,σ₁)
Приоритеты: нормальное распределение для fᵢ и равномерное — для μ и σ.
Эксперименты
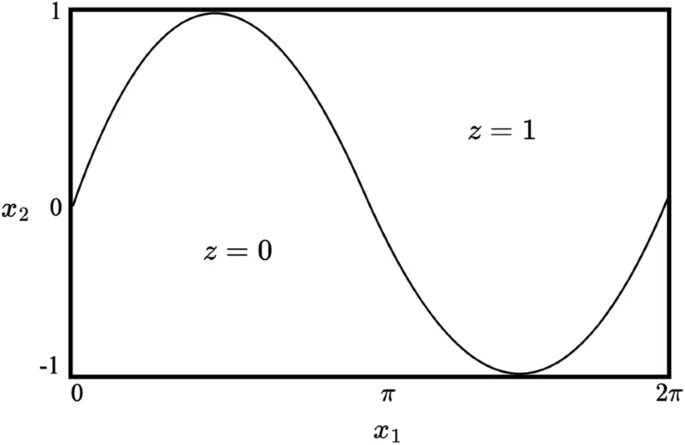
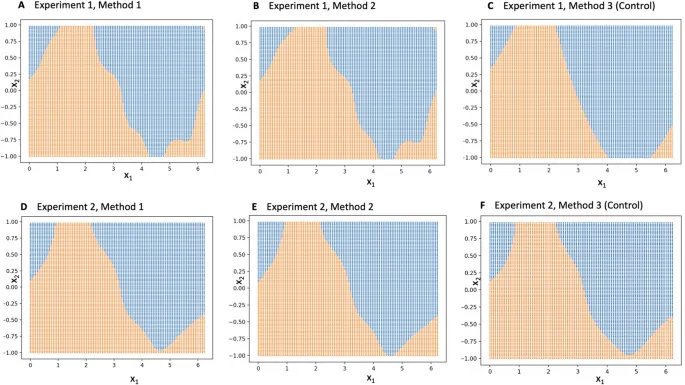
На синтетических данных с нелинейными границами (синусоида) проведено два эксперимента с разными распределениями параметров аннотаторов. Методы сравнены с SVGPR по:
- Среднеквадратичной ошибке (MSE) параметров.
- Точности, чувствительности и специфичности классификации.
Результаты
Метод 2 показал меньшую MSE для скорости дрейфа (0.0684 против 0.0755 в эксперименте A), но большую для диффузии. Точность предсказания меток достигла 99.1%, а классификатора — 97.6%.
Обсуждение
Использование модели дрифф-диффузии позволяет не только оценить надежность аннотаторов, но и прогнозировать их нейробиологические маркеры. Ограничения включают высокую вычислительную сложность и необходимость валидации на реальных данных.
