Модели принятия решений с непрерывным ответом: теория и оценка параметров

Введение в модели непрерывного принятия решений

Люди часто принимают решения между непрерывными альтернативами. Эти решения с непрерывным ответом встречаются во многих повседневных ситуациях. Например, при принятии инвестиционных решений люди определяют, какую часть своих финансовых ресурсов они хотят вложить в определенный фонд или акцию. Альтернативно, люди иногда решают о цене, по которой они готовы продать предмет (например, автомобиль). В экспериментальных условиях задачи принятия решений с непрерывным ответом часто представляют собой упрощение повседневных ситуаций, такие как исследования зрительной рабочей памяти, где людей просят вспомнить направление, ориентацию, местоположение или цвет стимула по непрерывной шкале.

Важно отметить, что решения с непрерывным ответом предоставляют значительно больше информации, чем их аналоги с дискретными решениями, что привело к их растущей популярности в экспериментальной психологии. Например, непрерывный ответ уже часто использовался в различных исследованиях численного познания, восприятия движения и восприятия ориентации. Поскольку решения с непрерывным ответом также могут применяться ко многим реальным ситуациям и предоставляют много информации о когнитивных процессах, они представляют собой важную эмпирическую тему исследования.

Модели последовательной выборки в принятии решений

В исследованиях принятия решений модели последовательной выборки стали доминирующей теоретической основой для понимания того, как люди принимают решения в ситуациях с двумя или несколькими альтернативами. Эти модели предполагают, что лицо, принимающее решение, с некоторой скоростью (часто называемой скоростью дрейфа) выбирает зашумленные доказательства из окружающей среды, и как только количество интегрированных доказательств для одного варианта превышает порог (известный как порог принятия решения), решение принимается.

Недавно модели последовательной выборки были расширены для решений с непрерывным ответом. Были сделаны различные предложения для этой цели, такие как двумерная круговая диффузионная модель и ее n-мерное обобщение - гиперсферическая диффузионная модель, пространственная непрерывная диффузионная модель, модель радиальной основы с протекающими конкурирующими аккумуляторами и модель накопления с множественными якорями. Хотя каждая разновидность имеет разные сильные и слабые стороны, в текущей работе основное внимание уделяется гиперсферической диффузионной модели по нескольким причинам.

Преимущества гиперсферической диффузионной модели

• Математическая управляемость функции правдоподобия в гиперсферической диффузионной модели делает ее простой в обработке и оценке
• Модель обеспечивает прямое соответствие между шкалой ответа в модели и экспериментальной шкалой ответа
• Модель успешно описывает различные экспериментальные результаты в рабочей памяти, памяти источника, случайном точечном движении и задачах ценообразования

Динамический порог принятия решения

Традиционно модели последовательной выборки предполагали, что решения людей лучше всего описываются фиксированными порогами принятия решений. Соответственно, предполагалось, что люди всегда накапливают одинаковое количество доказательств, независимо от требуемого времени, чтобы принять решение. Недавно утверждалось, что порог принятия решения уменьшается со временем, так что после некоторого времени требуется меньше доказательств.

Конкретно, эти коллапсирующие пороги - и подобные предложения, такие как сигналы срочности - предполагают, что через некоторое время люди чувствуют необходимость принять решение. Коллапсирующие пороги также были мотивированы нормативными соображениями; specifically, когда качество поступающих доказательств неизвестно и/или варьируется между вариантами, то коллапсирующие пороги обеспечивают наиболее эффективную стратегию обработки информации.

Эмпирические доказательства коллапсирующих порогов

Эмпирические доказательства коллапсирующих порогов - или других стратегий принятия решений, когда срочность возрастает со временем - были неоднозначными. В то время как некоторые исследования обнаружили доказательства в пользу коллапсирующих порогов, другие обнаружили противоположное или обнаружили, что люди, по-видимому, принимают коллапсирующие пороги только при определенных условиях задачи, таких как наличие сроков принятия решений или акцент на срочности. В целом, вопрос о том, чувствуют ли люди большую срочность с течением времени для принятия решения, продолжает обсуждаться в исследованиях принятия решений.

Гиперсферическая диффузионная модель: математические основы

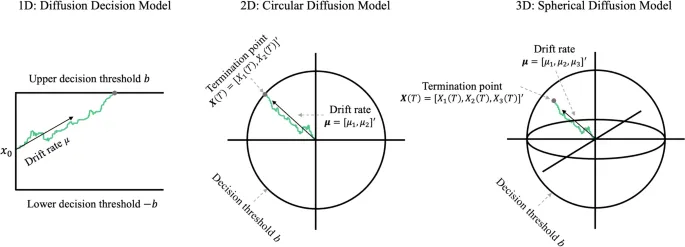
Гиперсферическая диффузионная модель представляет собой n-мерное расширение хорошо известной диффузионной модели принятия решений. Модель диффузионного принятия решений предназначена для объяснения процесса принятия решений в сценариях выбора из двух альтернатив и применялась в широком диапазоне областей, связанных с принятием решений.

Конкретно, модель диффузионного принятия решений предполагает, что единственный относительный аккумулятор интегрирует зашумленные доказательства в пределах одномерного пространства доказательств с постоянной средней скоростью, называемой скоростью дрейфа, пока аккумулятор не достигнет одного из нижних или верхних порогов, и затем принимается соответствующее решение. В этой модели величина скорости дрейфа указывает, насколько силен входной сигнал. Другими словами, более сильный входной сигнал дает более высокое значение скорости дрейфа, что предсказывает более быстрые и точные ответы.

Математическая формулировка процесса

Процесс накопления в этой модели можно сформулировать с помощью одномерного винеровского процесса следующим образом: dX(t) = μdt + σdW(t), где X(0)=x₀, σ - коэффициент диффузии и определяет уровень шума во время накопления доказательств, а dW(t) - процесс Винера.

Накопительный процесс, рассмотренный в уравнении, объясняет только время принятия решения. Однако время ответа также отражает некоторые дополнительные компоненты, которые не связаны напрямую с процессом принятия решения, такие как время кодирования и время моторного выполнения. Соответственно, модель диффузионного принятия решений рассматривает общее время кодирования и моторное время как дополнительный параметр, называемый временем не-решения.

Расширение до многомерного пространства

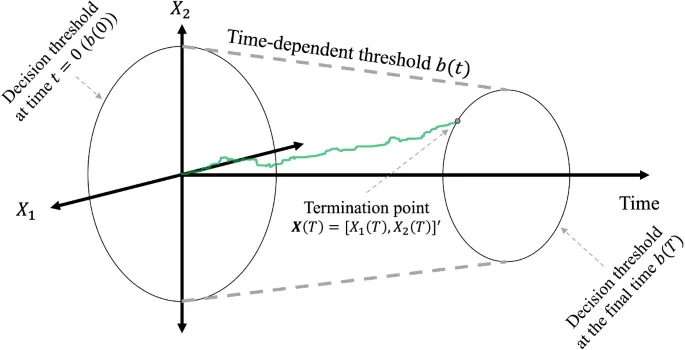
Гиперсферическая диффузионная модель расширяет одномерный процесс Винера в модели диффузионного принятия решений до многомерного процесса Винера, где процесс накопления происходит within a hypersphere. Другими словами, процесс накопления доказательств в гиперсферической диффузионной модели представлен n-мерным векторно-значным процессом Винера, флуктуирующим within an n-мерной гиперсферы.

Модель предполагает, что процесс накопления начинается из начала координат и продолжает накапливаться до тех пор, пока евклидово расстояние аккумулятора от начала координат не станет greater than порога принятия решения. Поэтому, когда процесс достигает точки на поверхности гиперсферы, процесс останавливается, и выбирается соответствующая точка на шкале ответа.

Параметры модели и их интерпретация

Подобно модели диффузионного принятия решений, порог принятия решения представляет, как люди могли调整 свой компромисс скорость-точность, уменьшая радиус, чтобы стать быстрее, или увеличивая радиус, чтобы стать более осторожными. Следует отметить, что в задачах с непрерывным ответом нет бинарного определения точности, и обычно она измеряется абсолютным/квадратичным отклонением от правильного ответа.

Следовательно, компромисс "скорость-точность" можно рассматривать как более обобщенный компромисс "скорость-дисперсия" для задач с непрерывным ответом, где более высокий порог принятия решения приводит к более медленным и более последовательным решениям, а более низкий порог принятия решения приводит к более быстрым ответам с большей вариабельностью ответов.

Метод интегрального уравнения для гиперсферической диффузионной модели

Чтобы получить функцию правдоподобия для гиперсферической диффузионной модели с зависящим от времени порогом, мы использовали подход, аналогичный предложенному Смитом. Сначала мы оцениваем распределение времени первого прохождения для гиперсферической диффузионной модели с нулевым дрейфом с зависящим от времени порогом, а затем, используя теорему замены меры Гирсанова, получаем совместную вероятность времени ответа и выбора.

Преобразование процесса Бесселя в процесс Феллера

Чтобы получить интегральное уравнение, соответствующее n-мерному процессу Винера с нулевым дрейфом, вместо рассмотрения расстояния от начала координат мы рассматриваем квадрат расстояния от начала координат. Этот процесс известен как процесс квадрата Бесселя. Затем, используя лемму Ито для производной, мы можем вывести следующее одномерное стохастическое дифференциальное уравнение.

Этот процесс является special case процесса типа Феллера с скоростью дрейфа, равной n, бесконечной infinitesimal дисперсией и пространством состояний. Поскольку Y(t) является квадратом расстояния от начала координат, то время первого прохождения определяется как момент, когда Y(t) достигает или превышает квадрат порога.

Результаты исследования моделирования

Чтобы оценить производительность предложенного метода интегрального уравнения, мы провели исследование восстановления параметров для гиперсферической диффузионной модели с постоянным порогом. Мы сгенерировали искусственные данные из модели с известными параметрами, а затем оценили параметры модели на основе смоделированных данных, используя метод максимального правдоподобия с предложенным методом интегрального уравнения.

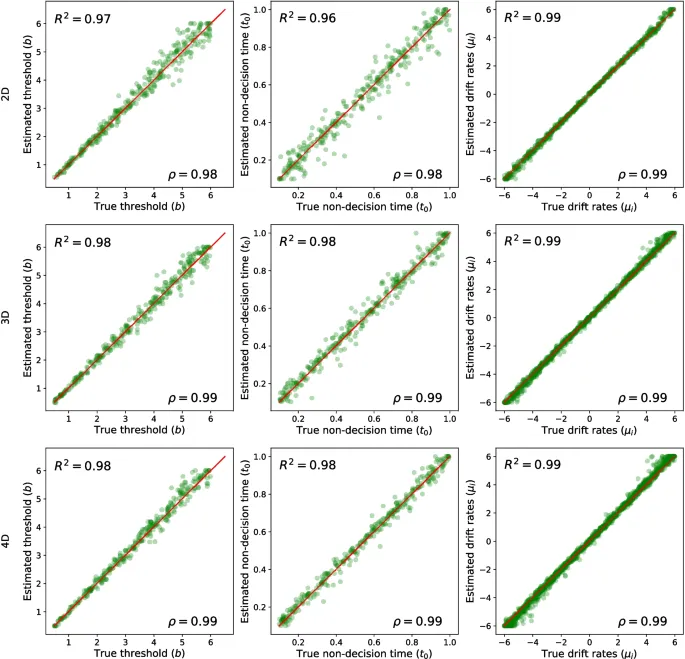
Восстановление параметров для моделей с постоянным порогом

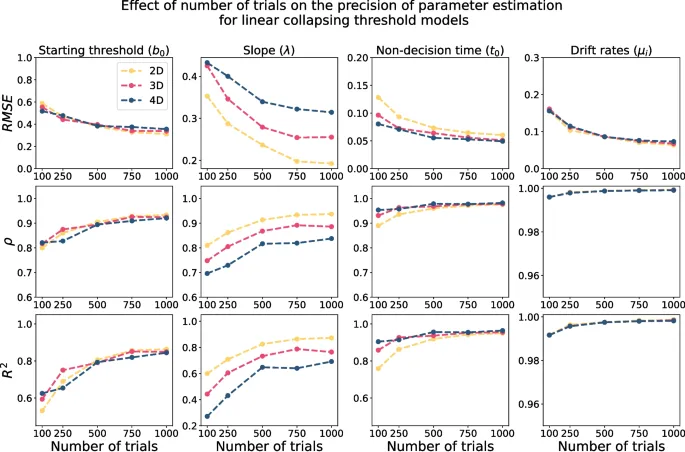
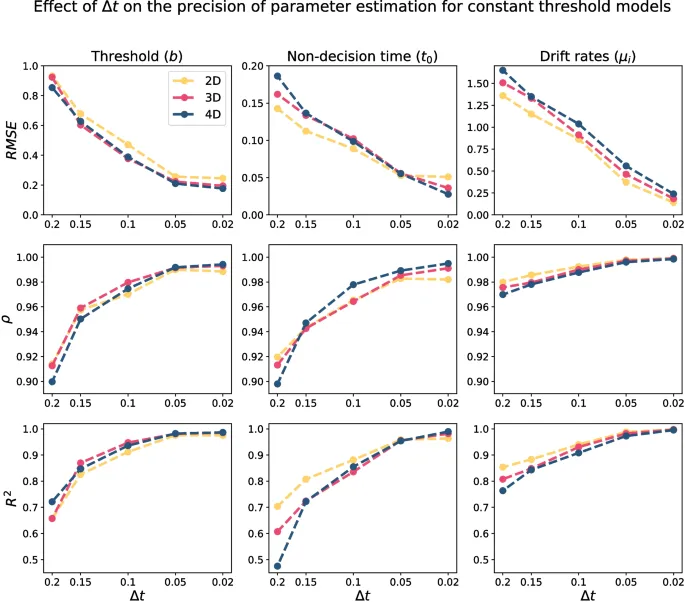
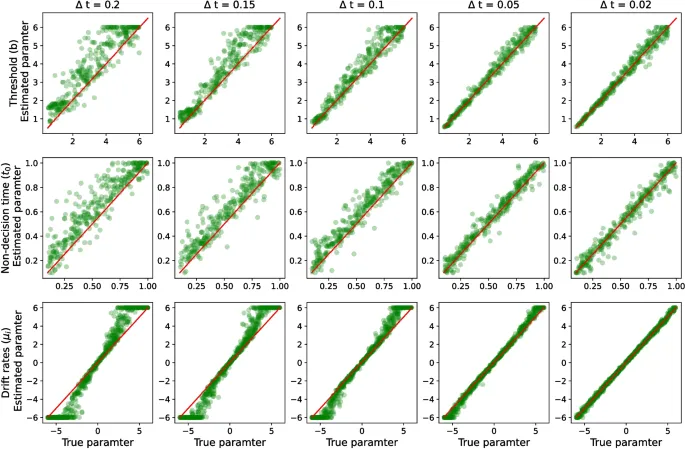
Результаты показывают, что предложенный метод интегрального уравнения может точно восстановить параметры гиперсферической диффузионной модели с постоянным порогом. Все параметры были восстановлены с высокой точностью, с низкой среднеквадратичной ошибкой, высокими значениями корреляции и R-квадрата, демонстрируя точную общую производительность восстановления.

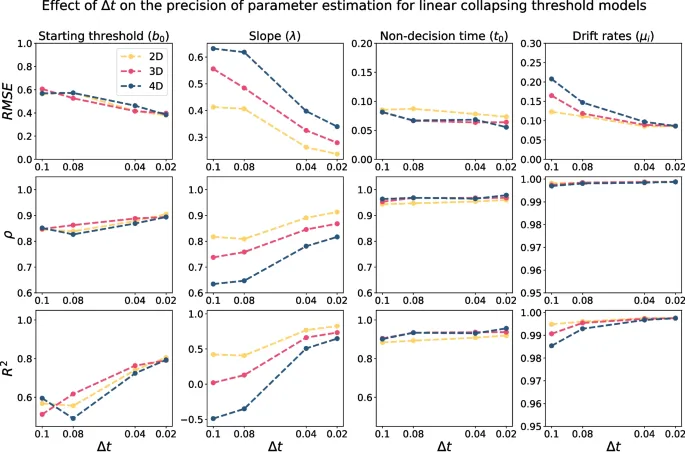
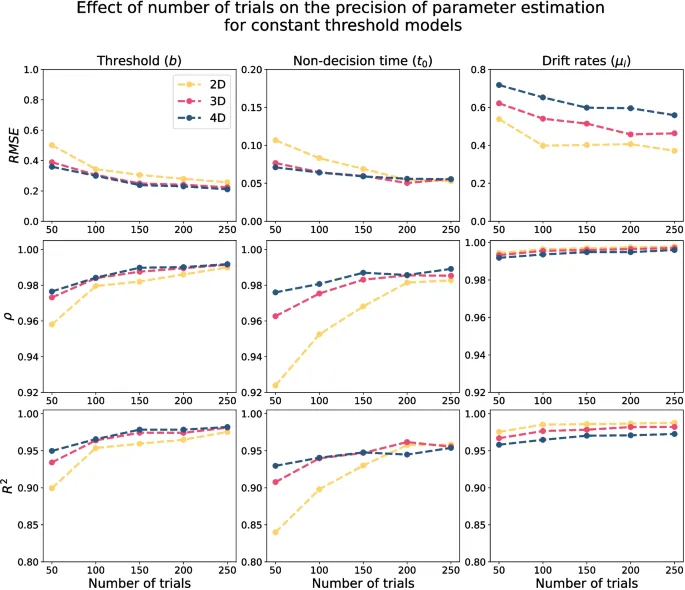
В дополнение к количеству trials, поскольку точность приближения времени первого прохождения связана с Δt, мы также оценили чувствительность восстановления параметров к значению Δt. В целом, результаты показывают, что чем меньше значение Δt, тем лучше оценка параметров, при этом среднеквадратичная ошибка, корреляция и R-квадрат систематически улучшаются, и часто с большими отступами, по мере уменьшения Δt.

Модели с зависящим от времени порогом

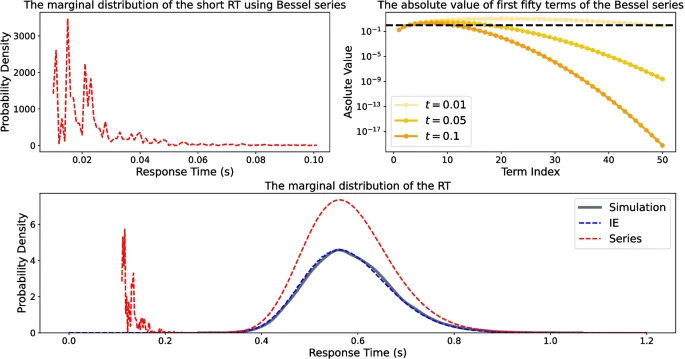
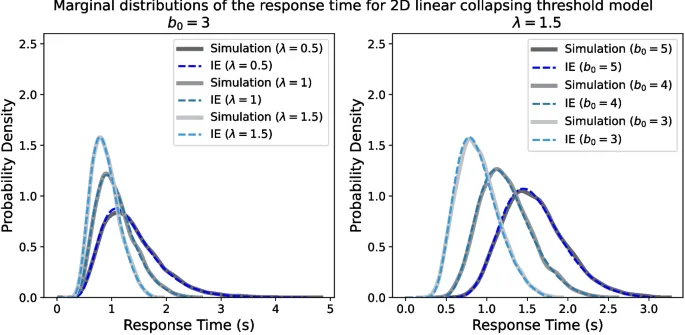
В качестве доказательства концепции, чтобы убедиться, что метод интегрального уравнения обеспечивает reasonably точное приближение функции правдоподобия для модели с коллапсирующим порогом, мы посмотрели, насколько closely функция правдоподобия метода интегрального уравнения соответствует данным, смоделированным из моделей. Важно отметить, что соответствие между моделированием модели и функцией правдоподобия метода интегрального уравнения extremely близко, показывая успех метода на уровне доказательства концепции.

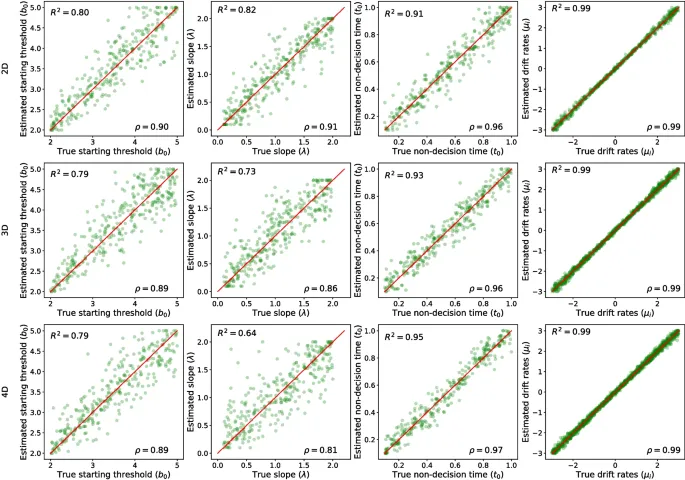
Восстановление параметров для коллапсирующих моделей

Результаты иллюстрируют качество восстановления параметров на основе 500 trials для линейных коллапсирующих гиперсферических диффузионных моделей с использованием метода интегрального уравнения. Интересно, что параметр скорости дрейфа восстанавливается extremely хорошо across всех моделей, что согласуется с результатами для линейной коллапсирующей модели диффузионного принятия решений. Все другие параметры двумерной и трехмерной гиперсферической диффузионной модели восстанавливаются reasonably хорошо.

Общее обсуждение и выводы

Понимание того, adjust ли люди свой порог принятия решения в течение времени принятия единственного решения, является одной из центральных тем, которые изучались в экономике, neuroscience и когнитивной психологии на протяжении многих лет. Однако большинство этих исследований были сосредоточены на решениях с бинарным выбором, при этом более сложные решения с непрерывным ответом в значительной степени игнорировались из-за отсутствия методологии для оценки зависящих от времени параметров в моделях с непрерывным ответом.

Эта работа разработала методологию, которая позволяет greater интеграцию этих отдельных областей исследования, где мы рассмотрели гиперсферическую диффузионную модель - модель последовательной выборки решений с непрерывными шкалами ответа - и introduced аналитическое решение для гиперсферической диффузионной модели с зависящим от времени порогом.

Преимущества и ограничения метода

Предложенный метод оценки имеет several преимуществ по сравнению с другими существующими методами. Во-первых, есть теоретическая гарантия, что решение интегрального уравнения сходится к распределению времени первого прохождения рассматриваемого процесса. Поэтому, рассматривая smaller Δt, можно получить more precise оценку распределения времени первого прохождения. Во-вторых, advantage - lower вычислительная стоимость. В-третьих, advantage - гибкость метода, так как метод интегрального уравнения может быть использован как для моделей с постоянным, так и с коллапсирующим порогом.

Несмотря на недавние достижения в вычислительных моделях для решений с непрерывным ответом, эти модели имеют некоторые challenges в оценке параметров. Настоящая работа рассмотрела гиперсферические диффузионные модели с постоянными и зависящими от времени порогами и предложила метод интегрального уравнения для оценки параметров. Чтобы evaluate метод, мы провели исследование восстановления параметров для моделей с постоянным или зависящим от времени порогом. Результаты demonstrated, что метод интегрального уравнения relatively быстрый, точный и надежный в оценке параметров гиперсферических диффузионных моделей.