Ожидаемое приращение информации в тестах остроты зрения и контрастной чувствительности: сравнение методов

Введение в измерение информации

Измерение служит краеугольным камнем научного метода и находит применение в самых разнообразных дисциплинах, включая физику, биологию, инженерию, социальные науки и медицину. Оно предоставляет эмпирические данные, необходимые для проверки гипотез, формулирования теорий, оценки эффективности и диагностических процедур. Несмотря на разработку многочисленных метрик качества, предназначенных для оценки отдельных измерений и согласованности между двумя одномерными измерениями, задача сравнения инновационных измерений с установленными золотыми стандартами остается сложной проблемой. Эта проблема особенно ярко выражена, когда новые измерения дают результаты иной или большей размерности. Более того, традиционные метрики, такие как те, которые оценивают вариабельность при повторном тестировании, в первую очередь количественно определяют неопределенности, связанные с результатами измерений, и не включают в себя оценку знаний, полученных в процессе измерения.

Информационная теория и измерение

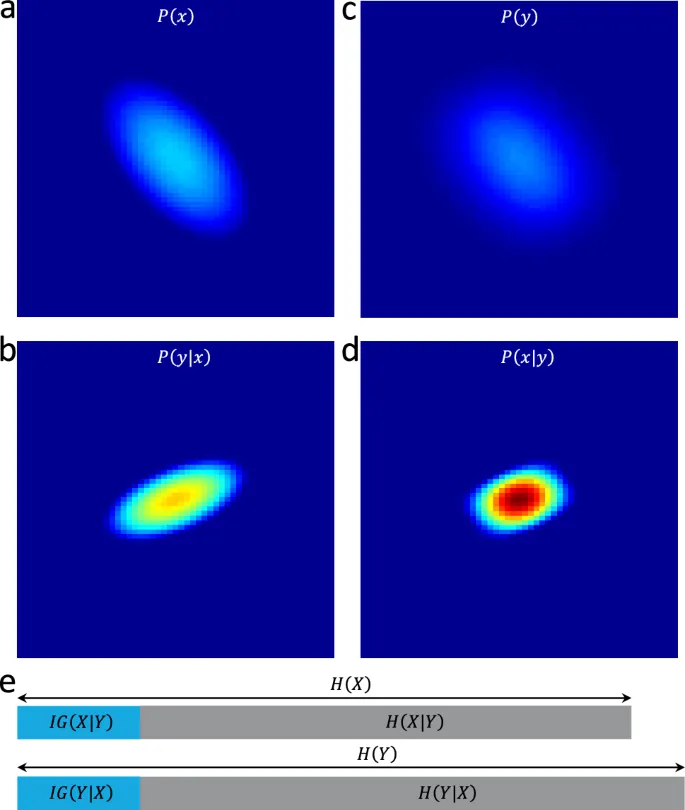
Рассматривая через призму теории информации, измерение концептуально определяется как «набор наблюдений, которые уменьшают неопределенность, а результат выражается в виде количества». Чтобы точно количественно оценить объем новых знаний, полученных в результате измерения, мы предлагаем применение концепции ожидаемого приращения информации, также известного как ожидаемая взаимная информация. Хотя концепция приращения информации нашла широкое применение в машинном обучении, где она служит фундаментальным критерием для оптимизации деревьев решений и направляет выбор оптимальных стимулов в алгоритмах активного обучения, ее применение в основном было сосредоточено на оценке относительного прироста информации среди различных функций или стимулов в процессе обучения. Однако в данном исследовании мы используем ее для количественной оценки объема информации, получаемой в результате измерений, проведенных на популяции.

Вычисление ожидаемого приращения информации

Существуют два эквивалентных метода расчета ожидаемого приращения информации. Первый подход основан на уменьшении неопределенности относительно измеряемого свойства, часто называемого «истиной», после проведения измерения. Второй подход основан на разнице между неопределенностью, связанной со всеми возможными результатами измерений в популяции, и projected остаточной неопределенностью после выполнения измерения. Хотя первый подход является прямым следствием концепции ожидаемого приращения информации, второй подход на практике往往 оказывается проще в реализации. Оба метода представлены ниже, а дополнительная проверка их эквивалентности приведена в Приложении 1.

Практическая иллюстрация ожидаемого приращения информации

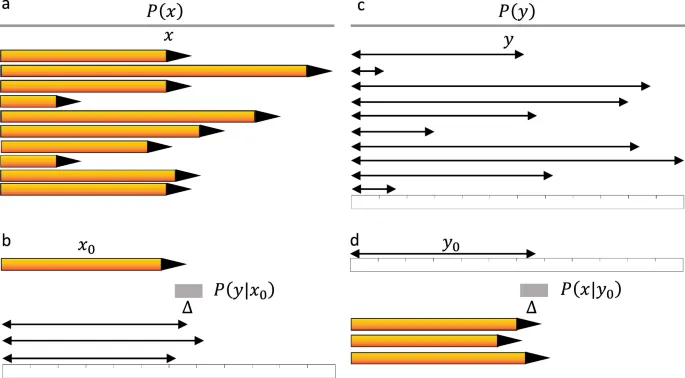
Мы представляем практическую иллюстрацию ожидаемого приращения информации с использованием двух линеек, рассматривая как первый, так и второй подходы. Для линейки с единицей измерения Δ распределение вероятности измерения объекта длиной x представлено как P(y|x) = U(x-Δ/2, x+Δ/2), где U(m, n) — равномерное распределение с границами m и n. Если эта линейка используется для измерения объектов с длинами от 0 до L с равной вероятностью, то распределение вероятности для длин объектов составляет P(x) = U(0, L). Энтропия X до любого измерения H(X) рассчитывается, и ожидаемое приращение информации вычисляется как IG(X|Y) = log₂(L/Δ).

Обзор текущего исследования

Ожидаемое приращение информации, которое количественно определяет знания, полученные в результате измерения, не ограничивается одномерными примерами. Его можно эффективно использовать для сравнения измерений с любым уровнем размерности. В этом исследовании мы расширили его применение для оценки тестов остроты зрения (VA) и контрастной чувствительности (CS), которые по своей природе involve измерения с разной размерностью. Применяя ожидаемое приращение информации к тестам VA и CS, мы aimed предоставить количественную основу для сравнения этих тестов, учитывая их различные оптотипы, размерности результатов и их способность предоставлять ценные знания.

Тесты остроты зрения

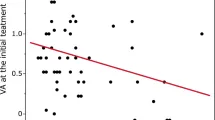
Острота зрения является crucial мерой зрительной функции и широко используется для диагностики и лечения заболеваний зрения, оценки эффективности лечения и установления профессиональных стандартов. Золотым стандартом теста является таблица ETDRS, состоящая из рядов по пять оптотипов одинакового размера, и используется для генерации одномерного показателя порога VA для каждого пациента. Однако представлен новый тест, называемый тестом qVA, который включает три оптотипа одинакового размера в каждом испытании и генерирует двумерную оценку, включающую порог VA и диапазон VA. Важно отметить, что это дополнительное измерение обеспечивает более комплексную оценку остроты зрения, и его игнорирование может привести к неполной оценке.

Тесты контрастной чувствительности

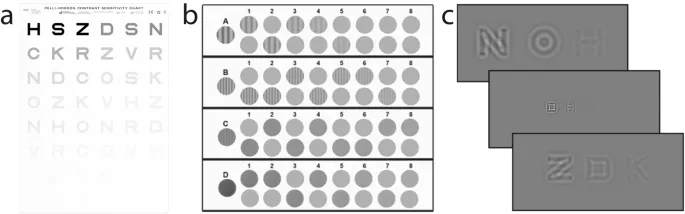
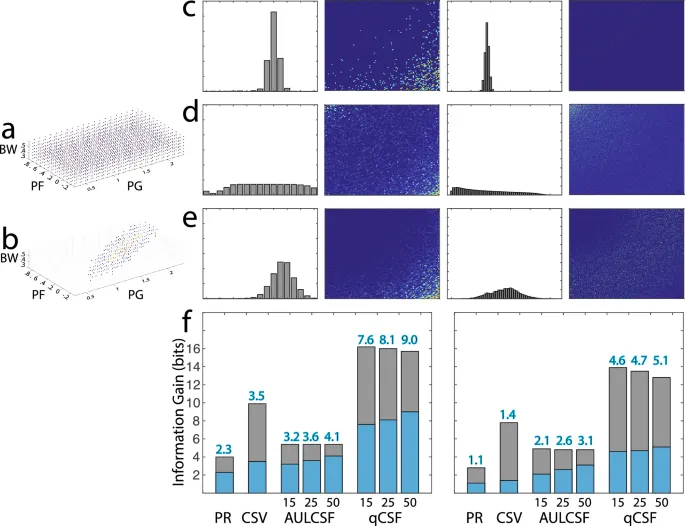
Функция контрастной чувствительности — это increasingly важная мера в клинических исследованиях и клинических trials, поскольку она предлагает более комплексную характеристику пространственного зрения по сравнению с VA. Было разработано несколько инструментов для измерения CS, каждый из которых использует разные оптотипы и produces оценки с разной размерностью. Например, тест Пелли-Робсон использует нефильтрованные стимулы букв Слоана и генерирует одномерный показатель CS на одной пространственной частоте, в то время как тест CSV1000 использует стимулы синусоидальных решеток с оконной функцией и provides четырехмерный показатель CS на четырех пространственных частотах. Другой тест, qCSF, использует фильтрованные стимулы букв Слоана и генерирует как одномерный показатель площади под логарифмической CSF (AULCSF), так и шестимерный показатель CS на шести пространственных частотах. Это разнообразие тестов CS и их размерностей результатов создает challenges при сравнении их эффективности.

Методы исследования

Все симуляции и анализы проводились на компьютере Dell с процессором Intel Xeon W2145 @ 3.70 ГГц (8 ядер и 16 потоков) и 64 ГБ установленной памяти (ОЗУ) с использованием Matlab R2019a (MathWorks Corp., Натик, Массачусетс, США) и R (R Core Team, 2020).

Симуляция наблюдателей для тестов остроты зрения

Мы провели две симуляции с использованием тестов Снеллена, ETDRS и qVA. В Симуляции 1 мы смоделировали 1386 наблюдателей из равномерного распределения порога VA и диапазона VA. В Симуляции 2 мы смоделировали 1386 наблюдателей из популяционного распределения порога VA и диапазона VA, полученного из существующего набора данных qVA 14 глаз, протестированных с помощью foil Бангертера.

Поведенческая функция остроты зрения

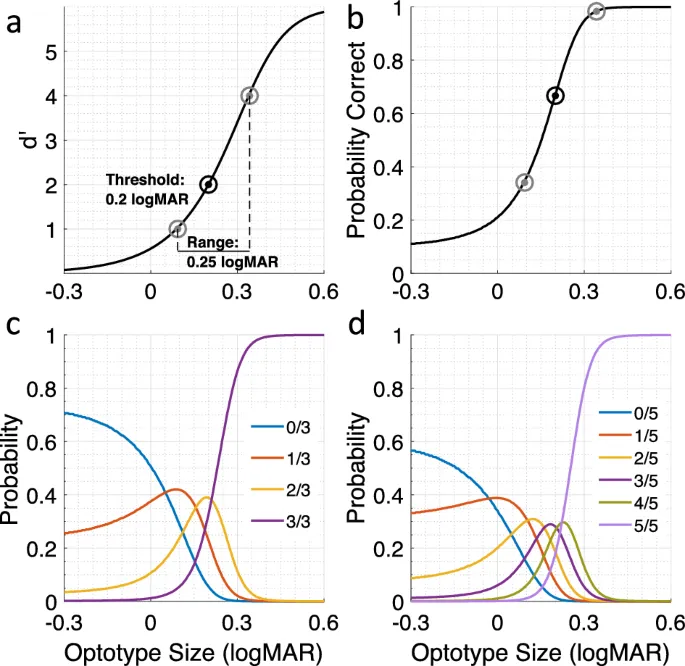
Для каждого смоделированного наблюдателя различимость (d′) для оптотипа размера s описывается поведенческой функцией VA. В этих тестах VA наблюдатели идентифицируют оптотипы из 10 букв Слоана. Мы можем вычислить вероятность получения m правильных ответов в задаче forced identification с 10 альтернативами в строке из M случайно выбранных оптотипов из их функции d′.

Таблица Снеллена

Таблица Снеллена имеет 11 строк с 1, 2, 3, 4, 5, 6, 7, 8, 8, 8 и 9 оптотипами в каждой строке и размером оптотипа от 1.0 до -0.3 logMAR. Каждый смоделированный наблюдатель тестировался по стандартной процедуре.

Таблица ETDRS

Таблица ETDRS имеет 14 строк с пятью оптотипами, с размером оптотипа от 1.0 до -0.3 logMAR. Каждый смоделированный наблюдатель тестировался по стандартной процедуре. Были смоделированы четыре различных правила прекращения теста.

Тест qVA

qVA — это байесовский тест остроты зрения с активным обучением. Его пространство стимулов состоит из оптотипов 91 линейно spaced размеров от -0.5 до 1.3 logMAR с разрешением 0.02 logMAR.

Вычисление приращения информации

Мы сначала вычислили P(y_j) из P(y_j|x_i) для каждого теста. Затем мы вычислили общую энтропию каждого теста для популяции. Ожидаемая остаточная энтропия была вычислена, и, наконец, было получено ожидаемое приращение информации.

Результаты тестов остроты зрения

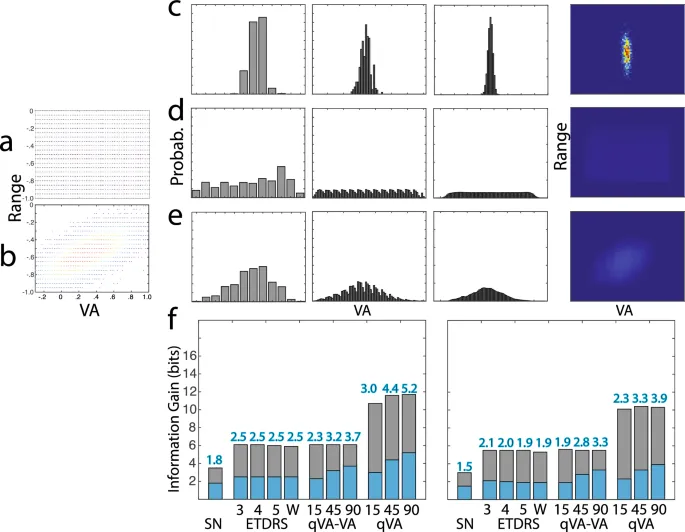
Распределения порога VA и диапазона VA наблюдателей в двух симуляциях показаны на Рис. 5a,b. На Рис. 5c показаны распределения результатов тестов P(y_j|x_i) одного репрезентативного смоделированного наблюдателя x_i в тесте Снеллена, ETDRS (правило 3 ошибок) и тесте qVA, с результатами из теста qVA, оцененными только по VA, и как по порогу VA, так и по диапазону VA. На Рис. 5d,e показаны распределения результатов тестов P(y_j) популяций в Симуляции 1 и 2 соответственно.

Общая энтропия H(Y), ожидаемая остаточная энтропия H(Y|X), ожидаемое приращение информации IG(Y|X), ожидаемое количество классов N(Y|X), среднее количество протестированных оптотипов, ожидаемое приращение информации на протестированный оптотип и отношение ожидаемого приращения информации к log₂ количества протестированных оптотипов для трех тестов в двух симуляциях перечислены в Таблице 1. Ожидаемое приращение информации IG(Y|X) также plotted на Рис. 5f.

Обсуждение

В этом исследовании мы представили концепцию из теории информации, называемую ожидаемым приращением информации (или взаимной информацией), чтобы количественно оценить объем новых знаний, которые можно получить из измерения популяции. Эта концепция позволяет нам сравнивать измерения с разной размерностью и оценивать потенциальные advantages новых измерений, которые генерируют distinct или данные higher размерности по сравнению с текущим золотым стандартом. Важно, что она focuses на actual знаниях, полученных в результате измерений, выходя beyond простое quantification неопределенностей измерений.

Мы продемонстрировали два эквивалентных подхода для вычисления ожидаемого приращения информации: (1) уменьшение неопределенности и (2) разница в неопределенности. В обоих подходах ключевая идея заключается в том, что ожидаемое приращение информации количественно определяет увеличение знаний, достигнутое в результате измерения. Этот прирост знаний больше, когда initially больше неопределенности и/или когда измерение effectively уменьшает эту неопределенность. Эти подходы provide rigorous и quantitative способ оценки ценности измерения в различных областях науки и beyond.

В качестве практического применения этой концепции мы вычислили и сравнили ожидаемое приращение информации от различных тестов VA и CS. Наши findings revealed некоторые intriguing insights: (1) Тесты VA: таблица ETDRS, текущий золотой стандарт, generated меньше ожидаемого приращения информации, чем тест qVA с 15 строками, indicating potential для улучшенной оценки VA с qVA. (2) Тесты CS: тест CSV1000 outperformed тест Пелли-Робсон, но тест qCSF с 25 trials продемонстрировал наибольшее ожидаемое приращение информации, showcasing его advantages в оценке CS.

Важно учитывать целевую популяцию при сравнении ожидаемого приращения информации, так как оно может варьироваться для разных популяций. Наши симуляции demonstrated эту зависимость, indicating, что разные целевые популяции могут require разные измерения, и разные измерения могут иметь advantages или disadvantages в разных популяциях. Поэтому при сравнении тестов crucial учитывать целевую популяцию вместе с измерительными инструментами. В этом исследовании мы использовали одни и те же целевые популяции для сравнения различных тестов VA и CS, и consistent порядок ранжирования тестов был получен across две популяции.

Ожидаемое приращение информации не ограничивается тестами зрения; оно может быть применено в различных областях. Например, оно может помочь сравнить newly разработанные тесты оптической когерентной томографии (OCT) с существующими, оценить способности различных тестов зрения классифицировать пациентов или оценить techniques анализа данных на основе их capacity уменьшать неопределенность.

Ожидаемое приращение информации может служить ценным инструментом для объективной оценки новых знаний, полученных в результате измерений. Оно может facilitate лучше сравнения и informed принятие решений в различных областях исследований и анализа данных.