Интересное сегодня
Аудиовизуальная интеграция и понимание прочитанного у детей ...
Введение Аутизм — это нейроразвивающееся состояние, характеризующееся различиями в социальной коммун...
Как стресс и невротизм влияют на когнитивные способности пос...
Влияние детских и взрослых травм на когнитивные функции Детские и взрослые травмы оказывают долгосро...
Трипофобия у детей 4-5 лет: научное исследование дискомфорта...
Введение в проблему трипофобии Дискомфорт при виде скоплений отверстий или кругов, таких как семенн...
Как Дональд Трамп изменил политический дискурс США: анализ н...
Введение: восприятие и реальность политического тона Подавляющее большинство американцев — 85% по да...
Низкий самоконтроль может вызывать депрессию и тревогу: иссл...
Как самоконтроль влияет на депрессию и тревогу? Многие люди замечают, что застревают в циклах тревож...
Игровое время и импульсивность как независимые, но взаимодоп...
Введение Гейминг стал популярным времяпрепровождением, с более чем 3 миллиардами геймеров по всему м...
Введение: Связь между пространством, временем и числами
Эволюционное давление, вероятно, способствовало формированию у человека эффективных механизмов представления количественных данных в областях пространства, времени и чисел. Существуют предположения, что эти области обладают общими характеристиками, указывающими на единую систему количественного представления (Walsh, 2003). Множество исследовательских линий подтверждают корреляции между ними (Cantlon et al., 2009; De Hevia et al., 2014; Dehaene & Brannon, 2011; однако см. Hamamouche & Cordes, 2019, предлагающий альтернативную гипотезу).
В этом контексте систематические когнитивные искажения могут свидетельствовать об общности или наличии общих компонентов в этих различных областях. Наше исследование фокусируется на широко известных ассоциациях между количеством/длительностью/порядком и пространством (Bonato et al., 2012, обзор). Эта ассоциация последовательно наблюдается в задачах, требующих категоризации одной из характеристик стимулов, таких как величина или четность для чисел, а также порядок или длительность для времени. Эти систематические искажения, как полагают, отражают основные характеристики, в данном случае пространственные, лежащих в основе представлений. В частности, при выполнении ответов с использованием левой конечности, они быстрее и точнее для относительно «малых», «коротких» или «ранних» элементов по сравнению с относительно «большими», «длинными» или «поздними» элементами, тогда как противоположное предпочтение обнаруживается при использовании правой конечности. Высказывались предположения, что окружающая среда играет важную роль в установлении этих ассоциаций, поскольку культуры, читающие справа налево, демонстрируют противоположное предпочтение как для чисел (Dehaene et al., 1993), так и для упорядоченных элементов (Guida et al., 2018). Тем не менее, картина, вероятно, более сложна, поскольку некоторые пространственно-количественные ассоциации (например, предпочтение определенного количества и пространственной позиции) могут возникать и при отсутствии культурного влияния, поскольку они наблюдаются у цыплят (Rugani et al., 2015), и их направление может гибко изменяться путем целенаправленных манипуляций (Fischer et al., 2010; см. также Ranzini et al., 2016).
Таким образом, накапливающиеся данные подтверждают взаимодействие нескольких разнородных факторов в определении ассоциации между временем/числами и пространством. Несмотря на некоторые методологические критики, эти ассоциации в основном исследовались с использованием латерализованных ответов (не только у людей, но и у животных). Многие ученые считают, что эти эффекты представляют собой поведенческий отпечаток пространственного представления, которое обычно соответствует направлению часто выполняемых движений или смещений внимания, таких как чтение и письмо (см. Bonato et al., 2012 для обзора). Эти ассоциации надежно обнаруживаются у здоровых испытуемых (Bonato et al., 2012; Vallesi et al., 2008), а также у неврологических пациентов. При наличии пространственных нарушений, вызванных, например, односторонним повреждением мозга, эти ассоциации становятся асимметричными, напоминая контрлатеральные пространственные нарушения, характеризующие нейропсихологический синдром, называемый пространственным игнорированием. У лиц с правосторонним повреждением мозга и левым игнорированием могут проявляться избирательные искажения для «ранних» или «коротких» элементов/длительностей, напоминающие дефициты, наблюдаемые при обработке контрлатерального пространства (Bonato et al., 2016; Marin et al., 2016; Saj et al., 2014; Zorzi et al., 2002, 2012).
Временной импульс: Новый взгляд на взаимодействие времени и арифметики
Широкое обнаружение пространственно-временных ассоциаций, охватывающих как временные длительности, так и упорядоченные во времени события (см. Previtali et al., 2010; van Dijck & Fias, 2011), указывает на удивительное сходство в ментальном представлении двух очень разных аспектов времени, а именно сенсорного и концептуального времени (Bonato & Umiltà, 2014). Хотя это сходство может предполагать наличие супрамодальных механизмов, поддерживающих обработку величин и длительностей, утверждалось, что повсеместность этих ассоциаций может быть результатом схемы ответа (Fischer et al., 2010). Вследствие этого, распространенной критикой этих ассоциаций является то, что пространственные аспекты могут быть не подлинными и спонтанно присутствующими, а скорее индуцированными, например, использованием бинарных, латерализованных ответов (Proctor & Cho, 2006).
Недавнее исследование Bonato et al. (2021) выявило новый маркер пространственно-временных взаимодействий в задаче, не требующей каких-либо латерализованных ответов, и, следовательно, не подверженной ранее упомянутому предполагаемому индуцированию пространственной ассоциации (для обсуждения этого вопроса см. Bonato et al., 2016; van Dijck & Fias, 2011). Эффект проявлялся не при обработке отдельных длительностей, а, скорее, являлся следствием сложения или вычитания длительностей, то есть выполнения временной арифметики. Участникам предлагалось складывать или вычитать длительность пар звуков в задаче воспроизведения времени, используя пары, которые давали бы одинаковую целевую длительность (например, 750 мс) для сложения (например, 600 мс + 150 мс) и вычитания (например, 1200 мс – 450 мс). Воспроизведенные длительности были значительно больше для задач сложения по сравнению с задачами вычитания. Это вновь обнаруженное временное искажение, названное «временным импульсом» (temporal momentum), было весьма значительным по величине (ошибка 20–40% в зависимости от длительности) и оставалось присутствующим после контроля за потенциальным искажением, вызванным самим знаком операции (+/-) и базовой ошибкой воспроизведения каждой целевой длительности без выполнения арифметических операций.
Эффект «временного импульса», выявленный Bonato et al. (2021), представляется аналогом эффекта «операционного импульса» (operational momentum) в числовой области, когда закономерность переоценки для сложения и недооценки для вычитания впервые была показана для операций над (несимвольными) визуальными численностями (McCrink et al., 2007), а затем распространена на арабские цифры (Knops et al., 2009). Термин «операционный импульс» был введен по аналогии с известным перцептивным искажением, известным как «репрезентативный импульс» (representational momentum), которое относится к тому факту, что положение движущегося объекта воспринимается искаженным вдоль его траектории (см. Hubbard, 2017 для обзора). Обнаружение концептуально похожего эффекта в темпоральной области, таким образом, предполагает тесную связь с пространством как для времени, так и для чисел. Как утверждается в работе Hubbard (2017), импульсоподобные эффекты являются поведенческим отпечатком супрамодального механизма, общего для разных областей, который реализует обработку движения в пространстве. Эта структура позволяет интерпретировать результаты временного импульса как, возможно, обусловленные смещением внимания вдоль ментальной временной линии, пространственно характеризующей течение времени (Bonato et al., 2012; см. также Guida et al., 2018b). Это отражает репрезентативный импульс в числовой области, который также интерпретируется как результат специфического для операций смещения направления/внимания (Knops et al., 2014; McCrink et al., 2007). Тем не менее, дальнейшее исследование эффекта временного импульса имеет решающее значение для обоснования интерпретации, связанной с вниманием. Примечательно, что другой эмпирический эффект предполагает ассоциацию между пространственным вниманием и арифметикой в форме латерализованных смещений внимания, модулируемых типом выполняемой арифметической операции (Masson & Pesenti, 2024, 2016). Эта пространственно-арифметическая ассоциация сравнивалась с операционным импульсом в нескольких исследованиях (обзор см. Haman & Lipowska, 2024; Prado & Knops, 2024). Однако результаты были неубедительными в поиске общего происхождения этих двух эффектов. В случае временного импульса любое сравнение с другими эффектами, приписываемыми пространственной обработке, остается на данный момент лишь гипотезой. Наши первоначальные результаты еще ждут воспроизведения, и возможно, что более короткие длительности, обнаруженные для задач вычитания, являются просто следствием характеристик стимулов. Например, убывающий порядок операндов мог вызвать эффект якорения относительно (самого короткого) второго операнда.
Цель исследования и методология
Целью данного исследования было дальнейшее расширение исследования эффекта временного импульса в двух онлайн-экспериментах. Как и в работе Bonato et al. (2021), участникам предлагалось складывать, вычитать или просто воспроизводить временную длительность звуковых стимулов (белый шум). Эксперимент 1 был прямой репликацией оригинального лабораторного исследования Bonato et al. (2021, Эксперимент 2). Онлайн-репликация также была призвана проверить надежность эффекта в условиях вариативности, вносимой аппаратурой и средой тестирования, специфичной для участников. Высокая вариативность аудиоустройств в сочетании с потенциальным фоновым шумом/гетерогенностью окружающей среды может стать проблемой для успешного воспроизведения первоначальных результатов. Эксперимент 2 был направлен на более глубокое понимание условий, вызывающих эффект временного импульса, и, в частности, на изучение влияния длительности операндов на временную арифметику. В нашем предыдущем исследовании наблюдалась явная модуляция в зависимости от длительности второго операнда, предполагающая, что эффект временного импульса подвержен влиянию перцептивного якорения (LeBoeuf & Shafir, 2006). Действительно, регрессионное моделирование продемонстрировало, что как тип операции, так и длительность второго операнда являются значимыми предикторами временных оценок. Кроме того, мы рассмотрели потенциальную роль возрастающих и убывающих длительностей. Этот эффект, например, был описан в эксперименте, сочетающем рисование линий с арифметикой (Shaki et al., 2015), где участники рисовали более длинную линию при сопоставлении с суммой с возрастающими по сравнению с убывающими операндами. В работе Bonato et al. (2021) возможность того, что порядок операндов играет роль для задач вычитания, не могла быть полностью отделена от эффекта длительности операндов, поскольку все задачи вычитания характеризовались вторым операндом, более коротким, чем первый. В результате участники сталкивались с двумя стимулами, длительность которых убывала, в то время как результат (результат вычитания) должен был быть всегда больше (в три или четыре раза) второго операнда. Импульсный эффект для вычитаний (результаты длительности короче, чем ожидалось) мог поэтому быть обусловлен эффектами якорения, которые не ограничиваются концептуальными оценками, но могут влиять, например, на визуальные пропорции и длительности времени, превышающие секунду (Thomas & Handley, 2008).
Методы
Исследование было одобрено Комитетом по этике психологических исследований Университета Падуи и проводилось в соответствии с принципами Хельсинкской декларации. Сбор данных проводился онлайн для обоих экспериментов. Участники были приглашены первым автором и получили ссылку для участия в каждом эксперименте по электронной почте. Все они дали информированное согласие до начала участия. Оба эксперимента были предварительно зарегистрированы на Open Science Framework (osf.io/4r2kh).
Программное обеспечение
- JsPsych framework (de Leeuw, 2015): использовался для разработки экспериментальных задач.
- Jatos framework (Lange et al., 2015): использовался для загрузки эксперимента.
- «jspsychpsychopshysics» plugin (Kuroki, 2021): позволял оптимизировать временные интервалы стимулов.
- R (R Core Team, 2021; RStudio Version 1.4.1106): использовался для анализа данных.
Критерии включения и исключения участников
Участники были не осведомлены о целях исследования. Для участия требовалось быть в возрасте от 20 до 30 лет и использовать веб-браузер «Chrome». Были установлены три априорных критерия для исключения участника в случае выполнения одного из следующих условий: (i) более 15% отбракованных проб; (ii) общая продолжительность эксперимента более 90 минут или менее 15 минут; (iii) выход из режима «полноэкранного режима» более 5 раз. Пробы отбраковывались для каждого участника, когда ответы выходили за пределы двух стандартных отклонений от индивидуального среднего для каждого условия и целевой длительности, а также когда начало ответа превышало 30 секунд.
Эксперимент 1: Репликация и проверка надежности
Выборка и количество проб
В Эксперименте 1 приняли участие 32 испытуемых (средний возраст 25,2 года, стандартное отклонение 2,42). Ни один участник не был исключен в соответствии с ранее описанными критериями. Каждый участник выполнил 144 пробы, разделенные на 9 блоков (3 блока для каждого условия операции). Каждое условие операции (сложение, вычитание, базовое/без операции/воспроизведение) включало 4 целевые длительности (600 мс, 750 мс, 900 мс, 1050 мс). Для каждой временной длительности было четыре комбинации (см. Таблицу 1). Задачи на сложение и вычитание предъявлялись в чередующихся блоках, порядок был контрбалансирован между участниками. Размер выборки и количество проб были рассчитаны в соответствии с выводами Bonato et al. (2021, Эксперимент 2) с использованием «контуров мощности», рассчитанных автоматическим инструментом (Baker et al., 2020).
| Условие | Операция | Длительность (мс) |
|---|---|---|
| Сложение | Операнд 1 + Операнд 2 | 400+200=600, 300+300=600, 200+400=600, 100+500=600 |
| 500+250=750, 375+375=750, 250+500=750, 125+625=750 | ||
| 600+300=900, 450+450=900, 300+600=900, 150+750=900 | ||
| 700+350=1050, 525+525=1050, 350+700=1050, 175+875=1050 | ||
| Вычитание | Операнд 1 - Операнд 2 | 800-200=600, 900-300=600, 1000-400=600, 1100-500=600 |
| 1000-250=750, 1125-375=750, 1250-500=750, 1375-625=750 | ||
| 1200-300=900, 1350-450=900, 1500-600=900, 1800-750=900 | ||
| 1400-350=1050, 1575-525=1050, 1750-700=1050, 1925-875=1050 | ||
| Базовый (воспроизведение) | 600 | |
| 750 | ||
| 900 | ||
| 1050 |
Задача временной арифметики
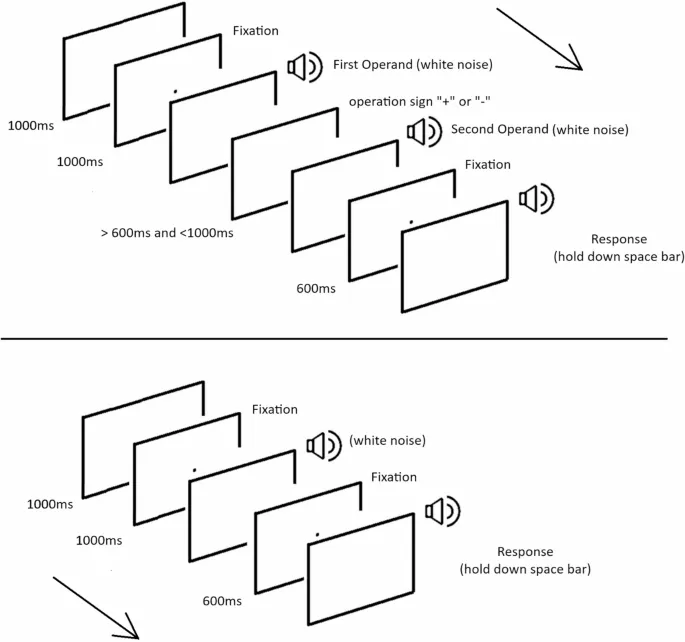
Процедура была идентична Эксперименту 2 в работе Bonato et al. (2021). Каждый испытание начиналось с сообщения «Подождите…» (1000 мс; на итальянском «Aspetta…»), затем предъявлялся фиксационный знак (1000 мс) и звуковой стимул (первый операнд). Затем появлялся символ «+» или «–» на случайный промежуток времени от 600 мс до 1000 мс. Эта случайная длительность была введена, чтобы избежать использования эвристик, основанных на общей длительности (Takahashi & Watanabe, 2015). Когда символ исчезал, воспроизводился второй звуковой стимул (второй операнд), за которым немедленно следовал фиксационный знак продолжительностью 600 мс. Затем сообщение «GO!» (на итальянском «VAI!») побуждало участника ответить, нажав на пробел на время, соответствующее результату операции (т.е. первый операнд /+ второй операнд). Во время нажатия на пробел слово «GO!» исчезало, и воспроизводился звуковой стимул до тех пор, пока не отпускался пробел (см. рис. 1 для схематического представления задачи). Участники были заранее проинформированы о типе блока (сложение, вычитание или базовый, т.е. без операции). В блоке вычитания первый операнд всегда был больше второго, чтобы избежать «отрицательных» длительностей. Каждый блок предварялся 9 тренировочными пробами.

Базовое условие (только воспроизведение/без операции)
После предъявления сообщения «Подождите…» (1000 мс) и фиксационного знака (1000 мс) воспроизводился звуковой стимул (белый шум) различной длительности. После предъявления еще одного фиксационного знака (600 мс) письменное сообщение «GO!» (VAI!) побуждало участника нажать на пробел. Когда участник нажимал на пробел, воспроизводился звуковой стимул, а слово «GO!» исчезало (см. рис. 1).
Стимулы
Временная длительность различных стимулов белого шума показана в Таблице 1. Обратите внимание, что каждая целевая длительность для «Вычитания» и «Сложения» определялась четырьмя различными комбинациями двух операндов. В условии «Сложение» половина пар характеризовалась вторым операндом, более длинным, чем первый, а в половине пар — наоборот. В «Вычитании» первый операнд всегда был длиннее, как и в работе Bonato et al. (2021).
Результаты Эксперимента 1
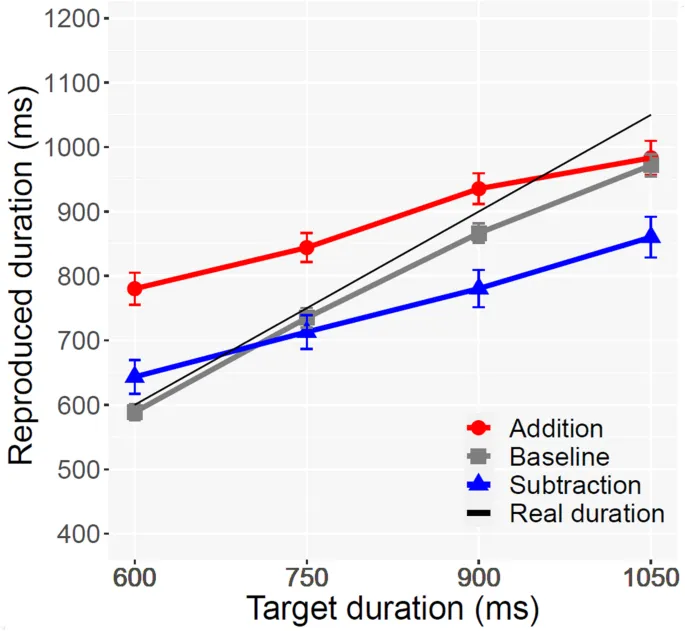
Ни один из участников не соответствовал предварительно зарегистрированным критериям исключения. В соответствии с критериями исключения проб, описанными выше, было удалено 2,67% проб. Ни один ответ не был удален из-за начала ответа > 30 с. Двухфакторный дисперсионный анализ с повторными измерениями с 4 условиями целевой длительности (600, 750, 900, 1050) и 3 условиями операции (Сложение vs. Вычитание vs. Базовый) в качестве факторов показал значимые основные эффекты целевой длительности [F(1,86,57,66) = 279,7, p < 0,001] и операции [F(2,62,79,98) = 77,6, p < 0,001]. Основной эффект операции был обусловлен тем, что воспроизведенные длительности были значительно больше в условиях сложения (M = 964 мс, SD = 158) по сравнению с базовым (M = 887 мс, SD = 146) и вычитанием (M = 885 мс, SD = 139), а также в базовом по сравнению с вычитанием. Таким образом, мы подтвердили эффект временного импульса, как и в Bonato et al. (2021). Взаимодействие между целевой длительностью и операцией также было значительным [F(6,189,17,61) = 8,5, p < 0,001]. Пост-хок тесты (парные t-тесты с коррекцией Бонферрони) показали, что разница между сложением и вычитанием была значительной для всех целевых длительностей (все p < 0,001). Разница между сложением и базовым также была значительной для всех целевых длительностей (все p < 0,001). Разница между базовым и вычитанием была значительной для 600 мс (t(31) = 2,36, p < 0,05), 750 мс (t(31) = 1,16, p > 0,05), 900 мс (t(31) = 3,0, p < 0,01) и 1050 мс (t(31) = 3,67, p < 0,001). Таким образом, вычитание приводило к недооценке относительно базового уровня для трех из четырех целевых длительностей.
Эффект якорения и порядок операндов: В работе Bonato et al. (2021) были обнаружены интересные результаты относительно порядка операндов в условиях вычитания. Там, где первый операнд всегда был больше второго (т.е. убывающая последовательность длительностей), наблюдалось значительное недооценивание. В нашем исследовании, несмотря на то, что порядок операндов не был сбалансирован в задачах вычитания (первый операнд всегда больше второго), мы также проанализировали влияние порядка, когда это было применимо. При сравнении пар с убывающим порядком операндов (например, 800-200) с парами с возрастающим порядком (не представленными в условиях вычитания, но теоретически возможными), наблюдались определенные тенденции. Однако, из-за несбалансированности в нашем дизайне, прямое сравнение было затруднено. Тем не менее, анализ показал, что когда второй операнд был значительно короче первого, оценка была ниже. Это может быть связано с эффектом якорения (LeBoeuf & Shafir, 2006; Oppenheimer et al., 2008), когда участники могут быть предвзяты последним услышанным стимулом и/или порядком операндов. Следует отметить, что, несмотря на эту разницу, обе комбинации характеризовались переоценкой. Действительно, даже сложения с порядком «большой-малый» (например, те, что приводили к более коротким оценкам: в среднем 857 мс) в любом случае оценивались как значительно более длительные, чем базовый уровень (790 мс; t(31) = 3,32, p < 0,01). Кроме того, все взаимодействия, включающие эксперимент, не были значимыми (все p > 0,2). Согласно этому ANOVA, два набора данных (собранные в присутствии vs. онлайн) не различаются.
Регрессионное моделирование
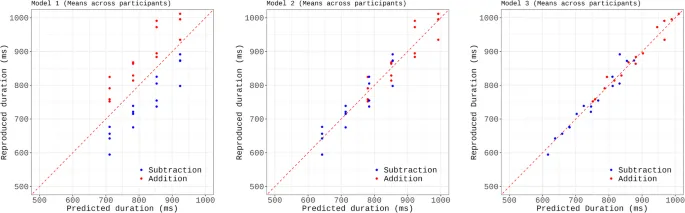
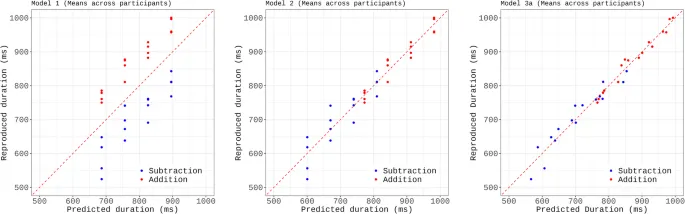
Мы использовали регрессионное моделирование для постепенного построения статистической модели, объясняющей роль различных переменных в прогнозировании воспроизведенной длительности для каждой операции (т.е. элемента). В то время как Bonato et al. (2021) использовали среднюю длительность по участникам, здесь мы использовали линейное смешанное моделирование (пакет R lmer, оценка максимального правдоподобия) для подгонки индивидуальных данных, включая испытуемого в качестве случайного эффекта. Выбор модели проводился пошагово, начиная с нулевой модели, имеющей только случайный перехват для испытуемого. Мы последовательно добавляли фиксированные эффекты и сравнивали вложенные модели с использованием тестов отношения правдоподобия (LRT). Диаграммы рассеяния (рис. 3) сравнивают прогнозы каждой модели с эмпирическими данными для каждой из 32 операций, отображая средние значения элементов (как наблюдаемые, так и прогнозируемые), усредненные по участникам. Включение целевой длительности улучшило соответствие (Модель 1 против Модели 0, LRT: χ²(1) = 258,71, p < 0,001) и не взаимодействовало с другими факторами. Затем мы добавили тип операции (Модель 2 против Модели 1, LRT: χ²(1) = 176,99, p < 0,001). Модель 2, включающая целевую длительность и тип операции, объяснила 57,4% дисперсии (условный R²). Таким образом, в этом случае, как и в Bonato et al. (2021), был подтвержден эффект временного импульса. В той же манере, как и для Эксперимента 1, мы не обнаружили значимого основного эффекта или взаимодействия, связанного с экспериментом, при сравнении текущего Эксперимента 2 с Экспериментом 2 в работе Bonato et al. (2021) (F(1,53) = 1,63, p > 0,05). Таким образом, закономерность результатов была стабильной независимо от модальности сбора данных и изменения операндов (вычитание).
Эксперимент 2: Влияние длительности операндов и порядка
Регрессионное моделирование
Как и в Эксперименте 1, мы использовали линейное смешанное моделирование (пакет R lmer, оценка максимального правдоподобия) для анализа данных временной арифметики. Мы также использовали этот подход для разделения потенциальных эффектов порядка операндов и длительности второго операнда. Хотя мы предсказывали эффект в том же направлении, порядок операндов является категориальным и предполагает смещение фиксированного размера, тогда как длительность второго операнда непрерывна и должна вызывать переменную смещение. Выбор модели проводился пошагово, начиная с нулевой модели, имеющей только случайный перехват для испытуемого. Мы последовательно добавляли фиксированные эффекты и сравнивали вложенные модели с использованием тестов отношения правдоподобия (LRT). Включение целевой длительности (Модель 1 против Модели 0, LRT: χ²(1) = 183,90, p < 0,001) и типа операции (Модель 2 против Модели 1, LRT: χ²(1) = 284,83, p < 0,001) значительно улучшило соответствие модели. На шаге 3 мы сравнили две невложенные модели: одну, включающую длительность второго операнда (Модель 3a), и одну, включающую порядок операндов (Модель 3b), при сохранении фиксированных эффектов из Модели 2. Оба предиктора улучшили соответствие модели по сравнению с Моделью 2, но их прямое сравнение с использованием информационных критериев показало лучшее соответствие для Модели 3a (AIC = 12826, BIC = 12855) по сравнению с Моделью 3b (AIC = 12832, BIC = 12861). Наконец, мы проверили, улучшило ли добавление порядка операндов к Модели 3a соответствие (Модель 4 против Модели 3a, LRT: χ²(1) = 0,02, p = 0,88). Это сравнение не выявило значительного улучшения, и Модель 4 имела более высокие значения AIC и BIC.
Следовательно, Модель 3a, включающая длительность цели, тип операции и длительность второго операнда в качестве фиксированных эффектов, и случайный перехват для испытуемого, была выбрана как наилучшим образом соответствующая модель (см. Таблицу 4). Остатки модели были нормально распределены (тест Шапиро-Уилка: W = 0,997, p = 0,22), а факторы инфляции дисперсии для фиксированных эффектов были низкими (все VIF < 1,6), что указывает на отсутствие проблем с мультиколлинеарностью. Выбранная модель объяснила 57,4% дисперсии в данных (условный R²), при этом фиксированные эффекты объяснили 27,6% дисперсии (маргинальный R²). Диаграммы рассеяния на рис. 5 сравнивают прогнозы вложенных моделей с эмпирическими данными для каждой из 32 операций, с средними значениями элементов (как наблюдаемыми, так и прогнозируемыми), полученными путем усреднения по участникам.

| Эффект | Оценка | Стд. ошибка | t-значение |
|---|---|---|---|
| Фиксированные эффекты | |||
| Intercept | 895,56 | 31,01 | 28,88 |
| Target Duration | 0,79 | 0,04 | 19,75 |
| Operation (Subtraction vs. Addition) | -81,60 | 6,70 | -12,18 |
| Second Operand Duration | 0,18 | 0,03 | 6,00 |
| Случайные эффекты | |||
| Subject (Intercept Std.Dev.) | 78,50 | ||
| Residual Std.Dev. | 105,80 | ||
Обсуждение Эксперимента 2
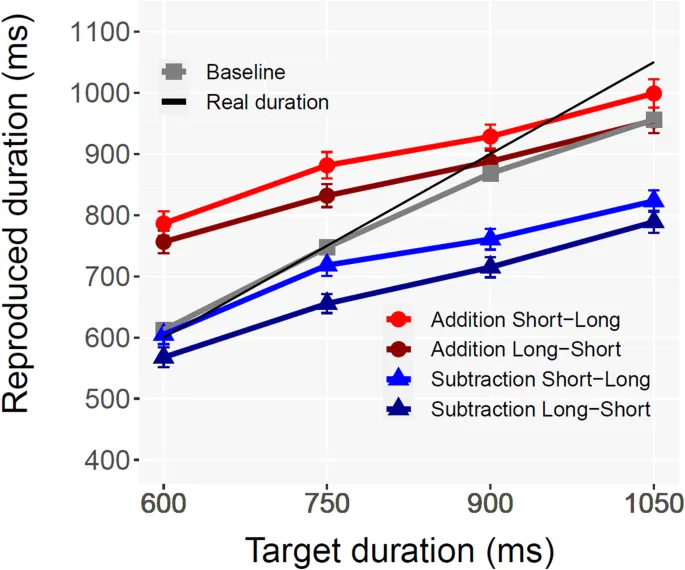
Результаты Эксперимента 2 подтвердили наличие арифметического временного импульса в полностью сбалансированном наборе стимулов (равное количество операндов с большей и меньшей длительностью) как для сложения, так и для вычитания. Для всех временных длительностей оценки были в среднем выше в условии «Сложение» по сравнению с условием «Вычитание». Кроме того, сравнительный анализ не выявил значительных различий с данными Эксперимента 1 (характеризующимися несбалансированными стимулами вычитания). Примечательно, что в условии «Вычитание» недооценка присутствовала даже при рассмотрении только проб, в которых второй операнд был длиннее первого. Это указывает на то, что для обеих операций эффект якорения не может объяснить закономерность переоценки и недооценки, специфичную для операций, которая в очередной раз ясно проявилась во втором эксперименте, расширяющем выводы Эксперимента 1 на набор полностью сбалансированных стимулов (включая задачи вычитания). Наконец, регрессионное моделирование на основе линейных смешанных моделей показало, что тип операции (сложение vs. вычитание) был решающим фактором для прогнозирования временных оценок. Длительность второго операнда была лучшим предиктором, чем порядок операндов, и последний не внес значительного улучшения при включении на последнем этапе.
Общее обсуждение: Природа временного импульса
В двух онлайн-экспериментах участникам предлагалось складывать или вычитать длительности пар звуковых стимулов (белый шум). Их производительность сравнивалась с базовым условием, требующим от участников воспроизведения отдельных звуковых стимулов на длительность, соответствующую правильному результату сложения/вычитания. Задача не имела латерализованных компонентов, поскольку участникам предлагалось нажать клавишу ответа для воспроизведения длительности, соответствующей арифметическому результату. Результаты подтвердили и расширили условия, приводящие к эффекту временного импульса — специфическому для операций искажению, характеризующемуся более длинными воспроизведенными длительностями для сложения, чем для вычитания, несмотря на одинаковые целевые длительности. Эксперимент 1 был прямой репликацией эксперимента, ранее проведенного в лаборатории. Эксперимент 2 включал новый набор стимулов, в том числе задачи вычитания с более короткими первыми операндами. В обоих экспериментах часть вариативности в ответах могла быть объяснена перцептивным эффектом якорения, при котором участники корректировали свои оценки в зависимости от длительности второго операнда. Порядок операндов известен как переменная, которая может существенно влиять на производительность (Shaki et al., 2015). Однако, помимо этого влияния, регрессионное моделирование на основе линейных смешанных моделей подтвердило, что наши данные могут быть удовлетворительно объяснены только при допущении искажения, специфичного для операций.
Эксперимент 2 включал использование полностью сбалансированного набора пар стимулов, включая более короткие первые операнды не только для сложения (как в Эксперименте 1), но и для вычитания. Соответственно, участникам предлагалось выполнить либо сумму, либо разность между двумя операндами (а не вычесть второй из первого, как в Эксперименте 1). Хотя эффект якорения все еще обнаруживался, результаты подтвердили наличие значительной модуляции, обусловленной типом выполняемой операции. Другими словами, более короткое воспроизведение в случае вычитания все еще присутствовало, когда вычитание включало равное количество проб с первым операндом длиннее, чем с более длинным вторым операндом. В условии «Вычитание» Эксперимента 2 искажение было более выраженным, когда второй операнд был короче, несмотря на отсутствие явных инструкций относительно порядка операндов (т.е. какой операнд из какого должен вычитаться). Линейное смешанное моделирование показало, что оценки в задаче временной арифметики значительно зависели от длительности второго операнда, которая поглотила предполагаемый эффект порядка операндов. Наш анализ показал, что люди склонны якориться на втором операнде (что приводит к большему переоцениванию, когда второй операнд имеет большую величину), в то время как, напротив, модель AHAB описывает эффект якорения на первом операнде (что приводит к обратному операционному импульсу). В заключение, модель AHAB не может объяснить наши результаты, ни полностью, ни экономно.
Наши выводы подтверждают выводы Bonato et al. (2021) и позволяют исключить альтернативные объяснения, связанные со стратегическими процессами. В широком смысле, исследования временного импульса значительно расширяют литературу, сообщающую о классических взаимодействиях между величинами и позицией ответа: первый эффект является «концептуальным» и не зависит от латерализованных ответов. Временной импульс представляет собой «уникум», в котором связь между испытанной длительностью и (предполагаемым) пространственным компонентом измеряется не напрямую, а является потенциальным объяснением переоценки/недооценки (т.е. присутствует только на концептуальном уровне).
Альтернативные модели
Модель «арифметических эвристик и искажений» (AHAB) (Shaki et al., 2018; см. также Mioni et al., 2021) предлагает альтернативное объяснение происхождения операционного импульса, описывая взвешенную комбинацию нескольких арифметических эвристик и искажений. AHAB предполагает, что операционный импульс в ментальной арифметике (а также временной импульс, если предположить общее происхождение) обусловлен тремя различными механизмами, активация которых зависит от конкретных условий:
- Эффект якорения: возникает, когда размеры результатов совпадают в разных операциях, и обусловлен якорением на первом операнде. Таким образом, AHAB предсказывает обратный операционный импульс с большими оценками для вычитания, чем для сложения. Стоит отметить, что в Shaki et al. (2018) первый операнд всегда был больше второго.
- Эвристика «больше-меньше»: обусловлена обычным повседневным опытом и предсказывает «классический» операционный импульс.
- Ассоциация знак-пространство: зависит от латерализованных ответов и отражает ассоциации «сложение/правое пространство» и «вычитание/левое пространство».
Как и в Mioni et al. (2021), наша парадигма временной арифметики избегает латерализованных ответов и, следовательно, ассоциация знак-пространство не может объяснить результаты. Кроме того, эффект оставался присутствующим после коррекции влияния знака (Bonato et al., 2021). Наконец, Эксперимент 2 показал идентичные эффекты при использовании сбалансированного набора пар стимулов. Это оставляет только эвристику «больше-меньше» как потенциальное объяснение результатов. При таких предпосылках модель AHAB предсказывает обратный операционный импульс для нашего Эксперимента 1 (из-за преобладающего присутствия эффекта якорения) и «обычный» операционный импульс для второго эксперимента (из-за присутствия эвристики «больше-меньше»). Предсказания для Эксперимента 1 не оправдались. Более того, наш анализ показал, что люди склонны якориться на втором операнде (что приводит к большему переоцениванию, когда второй операнд имеет большую величину), в то время как, напротив, модель AHAB описывает эффект якорения на первом операнде (что приводит к обратному операционному импульсу). В заключение, модель AHAB не может объяснить наши результаты, ни полностью, ни экономно.
Модель APiMA Prado и Knops (2024) предлагает другую перспективу. Согласно ей, эффекты операндов зависят конкретно от их порядка. В частности, воспринимаемая величина второго операнда (O2) будет зависеть от величины первого операнда (O1). Больший O1 вызовет недооценку O2, в то время как меньший O1 вызовет переоценку O2. Это, в свою очередь, повлияет на оцененный результат (помимо эффекта операции). Однако в случае Эксперимента 2 статистические доказательства эффекта порядка операндов были слабее, чем доказательства эффекта второго операнда при прямом сравнении с использованием информационных критериев. Более того, последний не был значимым, когда он был включен в качестве предиктора в модель, включающую длительность второго операнда. Таким образом, хотя наши результаты все еще могут быть интерпретированы в терминах последовательных зависимостей (Fornaciai & Park, 2020), которые влияют на арифметический расчет, мы заключаем, что эффект второго операнда является классическим примером эффекта якорения (LeBoeuf & Shafir, 2006), а не искаженного восприятия длительности второго операнда, предложенного моделью APiMA.
Как предложил один из рецензентов, мы могли бы быть (еще) более консервативными и избегать представления знака операции для каждой задачи, учитывая, что он варьировался только на уровне блока. Вторая, более теоретическая критика наших выводов может заключаться в том, что они слишком общие, поскольку, например, задачи «Вычитание» не всегда приводят к недооценке по сравнению с «Базовым» условием. Например, в Эксперименте 1 не было значимой разницы в средних оценках между двумя условиями. Однако два элемента указывают на обратное. Во-первых, в Эксперименте 2 появилась значительная разница между двумя условиями. Во-вторых, закономерность недооценки видна при рассмотрении индивидуальных временных длительностей. Те же соображения относятся к немногим случаям, когда условие «Сложение» не приводит к явной переоценке. Обратите внимание, что переоценка при сложении временных длительностей визуальных стимулов наблюдалась ранее (например, Takahashi & Watanabe, 2015), но ни одно исследование до Bonato et al. (2021) не исследовало вычитание временных длительностей. Примечательно, что Takahashi и Watanabe (2015) интерпретировали различия, найденные между базовыми условиями без сложения и условиями, характеризующимися несколькими сложениями, как эффект когнитивной нагрузки. В этом отношении ключевым вкладом данного исследования является демонстрация того, что недооценка при вычитании не может быть объяснена якорением или другими эвристиками. Это подразумевает, что общая закономерность, характеризующая эффект временного импульса, более экономно объясняется как результат арифметической обработки, и, в свою очередь, предполагаемого пространственного компонента в представлении временной длительности (Bonato et al., 2012). Применяется ли эффект временного импульса к более длительным промежуткам времени, характеризующим более экологические контексты, — это интригующий вопрос для будущих исследований.