Влияние распределения начальных оценок на "мудрость толпы" при социальном влиянии

Влияние распределения начальных оценок на "мудрость толпы" при социальном влиянии

Вопрос о том, когда и при каких условиях группы демонстрируют "мудрость толпы" (wisdom of the crowd), является центральным в исследованиях в области социальных и вычислительных наук. Значительная часть этих работ сосредоточена на роли социального влияния в усилении "мудрости толпы" или, наоборот, в заблуждении группы. Однако результаты этих исследований часто противоречивы, особенно когда речь идет о том, как структура социальной сети определяет степень влияния социального воздействия. В данной работе мы демонстрируем, что рассмотрение только структуры сети в изоляции недостаточно. Используя теоретический анализ, численное моделирование и повторный анализ четырех экспериментальных наборов данных (охватывающих в общей сложности 2885 испытуемых), мы приходим к выводу, что "мудрость толпы" критически зависит от взаимодействия между (i) централизацией сети социального влияния и (ii) распределением начальных индивидуальных оценок. Введя концептуальную рамку, объединяющую как структуру социального влияния, так и распределение начальных оценок, мы приводим ранее противоречивые результаты к единому теоретическому знаменателю и проясняем эффекты социального влияния на "мудрость толпы".

Введение

В своем классическом определении концепция "мудрости толпы" подразумевает, что агрегированная оценка группы индивидов может превосходить оценку отдельных, признанных экспертов^1,2. Недавние применения этой концепции включают технологическое, политическое и экономическое прогнозирование³, оценку эффективности⁴, выявление предпочтений⁵ и разработку государственной политики⁶.

Традиционные статистические подходы к объяснению "мудрости толпы" опираются на два следующих предположения:

• (i) индивидуальные ошибки некоррелированы или отрицательно коррелированы⁷;
• (ii) индивиды не имеют систематической ошибки (bias), то есть их средние ожидания верны².

Однако процессы социального влияния, в ходе которых люди обмениваются информацией о своих оценках, могут приводить к тому, что индивиды пересматривают свои суждения в задачах оценки^8,9,10,11,12. Следовательно, простое усреднение пересмотренных (после влияния) оценок отличается от простого усреднения начальных (до влияния) оценок.

Предшествующие исследования дали противоречивые результаты относительно влияния социального влияния на "мудрость толпы". Например, несмотря на свидетельства того, что социальное влияние может значительно улучшить групповые и индивидуальные оценки^{10,12,13,14,15,16,17}, также было установлено, что оно может вызывать систематические ошибки, стадное поведение (herding) и групповое мышление (groupthink)^8,9.

В ответ на эти несоответствия, заметные усилия по примирению результатов сосредоточились на исследовании того, как теории социальных сетей взаимодействуют с процессом формирования коллективных убеждений. Результаты этих усилий, включая основополагающие теоретические работы^11,18 и лабораторные эксперименты¹⁰, установили, что "мудрость толпы" сохраняется только в том случае, если влияние наиболее влиятельного индивида исчезает (т.е. становится незначительным) с ростом размера группы¹¹. Это условие выполняется в децентрализованных структурах влияния, где каждый имеет равный голос, в отличие от централизованных структур, в которых один или несколько индивидов имеют непропорциональное влияние. Интуитивно, "мудрость толпы" выигрывает от больших размеров группы, поскольку даже если индивиды в среднем имеют систематическую ошибку, дисперсия их коллективной оценки ниже; однако централизованное влияние снижает эту выгоду, сводя коллективную оценку к "мудрости немногих".

Хотя эти результаты, по-видимому, в целом указывают на превосходство децентрализованного влияния, их выводы основаны на предположении, что распределение начальных оценок сосредоточено вокруг истины. В таких ситуациях нет возможностей для улучшения толпы за счет социального влияния¹¹. Однако эмпирические распределения числовых оценок, как правило, являются правоскошенными (right-skewed) с избыточным эксцессом (excess kurtosis): большинство оценок низкие, а меньшинство находится на "толстом" правом конце^9,19,20. Скошенность распределения может возникать из-за систематической ошибки (тенденция переоценивать или недооценивать фактическое значение^19,21,22) или дисперсии (разброс оценок) в популяции. Следовательно, именно тогда, когда толпа изначально не сосредоточена вокруг истины, как наблюдается во многих эмпирических сценариях, централизованное влияние может представлять собой возможность для продвижения "мудрости толпы".

В данном исследовании мы задаемся вопросом, когда централизованные структуры влияния улучшают или ухудшают "мудрость толпы" в задачах оценки. Наши результаты демонстрируют, что эффект социального влияния систематически варьируется в зависимости от распределения начальных оценок и, следовательно, является более гетерогенным, чем предполагалось ранее. В частности, мы анализируем — теоретически, численно и эмпирически — влияние распределения начальных оценок на пригодность толпы для получения выгоды от централизации влияния.

Теоретическая модель

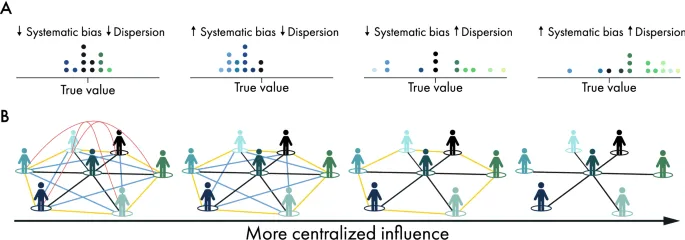
Для иллюстрации мы рассматриваем группу из n агентов, которым поручено с максимальной точностью оценить или спрогнозировать некоторую неизвестную положительную величину, такую как уровень безработицы в следующем квартале, ожидаемая продолжительность жизни больного пациента, количество калорий в еде, распространенность глобальных случаев гриппа через две недели или количество мармеладных бобов в банке. Чтобы смоделировать популяцию агентов, выполняющих конкретную задачу оценки, мы наделяем каждого агента начальной оценкой, основанной на смещенном и зашумленном сигнале относительно истины. Пусть группа из n агентов индексируется i = 1, dots , n, и обозначим их начальные оценки как {athbf {a}}_{i,0}. Начальные оценки являются независимыми и одинаково распределенными, и их общее распределение, {athcal {F}}_{u ,igma }^{ heta }, параметризовано неизвестной истиной heta, систематической ошибкой u и дисперсией igma. Параметр положения (u) указывает центр распределения, который смещает оценки относительно истины, а параметр формы (igma) определяет вариативность и форму хвостов распределения. Скошенность распределения может возникать из-за нескольких, возможно, взаимозависимых факторов: непропорциональное воздействие скошенной выборки экземпляра задачи^23,24, тенденция чрезмерно концентрироваться на информации, поддерживающей гипотезы²⁵, или уровень демонстративности данной задачи²⁶. В целом, начальные оценки можно рассматривать как неотъемлемые свойства контекста оценки: популяция агентов, выполняющих конкретный экземпляр задачи оценки. Различные популяции агентов, такие как эксперты и новички, могут иметь разные систематические ошибки и дисперсии для одного и того же экземпляра задачи. И наоборот, одна и та же популяция может различаться по своим систематическим ошибкам и дисперсии в различных экземплярах задач. Для краткости и абстрагирования агентов и задачи оценки, мы называем распределение начальных оценок "контекстом оценки". Рисунок 1A показывает четыре контекста оценки с различным уровнем систематической ошибки и дисперсии.

Агенты часто имеют доступ к мнениям или оценкам других агентов. Мы определяем коллективную оценку n агентов как среднее их пересмотренных (после влияния) оценок и обозначаем ее как {{athbf {a}}}^{n}. Во многих распространенных моделях социального влияния^11,18,27, а также в других механизмах агрегирования^7,28,29, коллективная оценка группы агентов может быть выражена как выпуклая комбинация (взвешенное среднее) начальных оценок: {{athbf {a}}}^{n}(athbf{w}) = um _{i=1}^{n}w_i{athbf {a}}_{i,0}, где w_1,dots ,w_n — положительные весовые коэффициенты, сумма которых равна единице. Эти весовые коэффициенты отражают влияние отдельных агентов на формирование коллективной оценки. Без потери общности мы предполагаем, что агенты упорядочены по убыванию их влияния, так что w_1 e w_2 e dots e w_n. Это определение коллективной оценки включает простое среднее начальных оценок — типичную "мудрость толпы" — как частный случай.

Мы вводим параметр централизации влияния, mega, чтобы интерполировать между коллективной оценкой, полученной в условиях полностью децентрализованной структуры влияния, где каждый агент имеет равный голос (т.е. mega = 0 и w_1 = w_2 = dots = w_n = 1/n), и диктаторской установкой с одним влиятельным агентом (т.е. w_1 =mega = 1 и w_2 = dots = w_n = 0). Чтобы исследовать роль централизации сети, 0 e mega e 1, мы рассматриваем класс структур влияния, индексируемых mega, таких что (см. SI Секция 1.1 для более подробной информации):

$$ {{athbf {a}}}^{n}(mega ) = mega {athbf {a}}_{1,0} + (1-mega )rac{1}{n}um _{i=1}^{n}{athbf {a}}_{i,0}. $$

Наше определение mega совпадает с централизацией Фримена³⁰ для класса типологий сетей, которые охватывают случаи, представляющие практический и эмпирический интерес, такие как полносвязные сети, звездные сети, пустые графы (изолированные индивиды) и круговые решетки, среди прочих. Рисунок 1B показывает четыре структуры влияния в этом классе (см. SI Секция S1.1 для расчета mega в различных сетях). Важно отметить, что это сети влияния (в которых связь между двумя людьми представлена взвешенным значением от нуля до единицы), а не сети коммуникации (т.е. бинарные сети, определяющие, кто с кем общается).

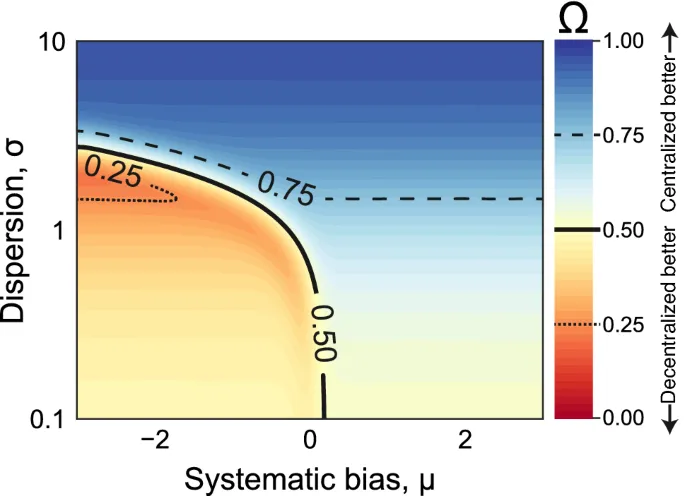
Мы измеряем коллективную производительность агентов с точки зрения близости коллективной оценки ({{athbf {a}}}^{n}) к истине ( heta). Учитывая контекст оценки (распределение начальных оценок), наш результат представляет интерес: превосходит ли коллективная оценка, полученная централизованной структурой влияния, децентрализованную базовую линию. Мы вычисляем вероятность этого исхода для данного контекста оценки и обозначаем ее как mega _n. Примечательно, что mega _n отражает критическую особенность контекста оценки, а именно его пригодность для получения выгоды от централизации. Когда mega _n > 1/2, толпа лучше приспособлена к децентрализованным структурам влияния; когда mega _n < 1/2, они лучше приспособлены к централизованным структурам влияния.

Результаты

Аналитические результаты

Наш теоретический анализ mega _n подтверждает, что для распределений с тяжелыми хвостами или правоскошенных распределений производительность коллективной оценки в централизованной структуре, где единственный агент имеет неисчезающее влияние (его вклад в коллективную оценку не стремится к нулю при n ightarrow nfty), превосходит децентрализованную базовую линию. В частности, для распределений с тяжелыми хвостами (например, Парето, лог-нормальное и лог-Лапласа) мы выявляем фазовые переходы, когда предельное значение нижней границы переходит от 0 к 1 или 1/2, когда параметр формы igma пересекает критическое значение (см. SI Секция S2.1). Интуитивно это связано с тем, что в децентрализованных сетях выборочное среднее распределения с тяжелыми хвостами доминирует из-за чрезмерного риска на хвосте (грубых ошибок нескольких индивидов). С другой стороны, при использовании взвешенных средних, как в централизованных структурах, мы можем гарантировать, что некоторые случайные индивиды оказывают достаточное влияние, чтобы предотвратить сильное отклонение агрегированной оценки группы от грубых ошибок немногих. Напомним, что в нашей модели индивиды имеют равные шансы занять центральную позицию, и, в частности, люди, чьи мнения чрезвычайно отличаются от большинства, очень немногочисленны и, следовательно, маловероятно, что займут центральное положение. Примечательно, что в этой модели централизованные структуры нарушают условие исчезающего влияния для "мудрости толпы"; см.¹¹ и SI Секция S2.15. Это подчеркивает важность предположений о распределении, которые зависят от контекста, при изучении влияния социального влияния на "мудрость толпы".

На Рисунке 2 мы иллюстрируем поведение mega _n для лог-нормального распределения начальных оценок, как сообщается в ряде эмпирических исследований^9,10,20. В этом случае mega _n предсказывает, что централизованные структуры влияния улучшают коллективные оценки по сравнению с децентрализованными, если распределение начальных оценок характеризуется систематической ошибкой переоценки или большой дисперсией (см. SI Секцию S2.2.1 и Рисунок S2 для влияния систематической ошибки). Однако эта зависимость меняется на противоположную, когда распределение начальных оценок характеризуется низкой дисперсией и систематической ошибкой недооценки (см. SI Секции S2.2 и Рисунок S1 для деталей симуляции и других классов распределений).

Повторный анализ четырех экспериментальных наборов данных

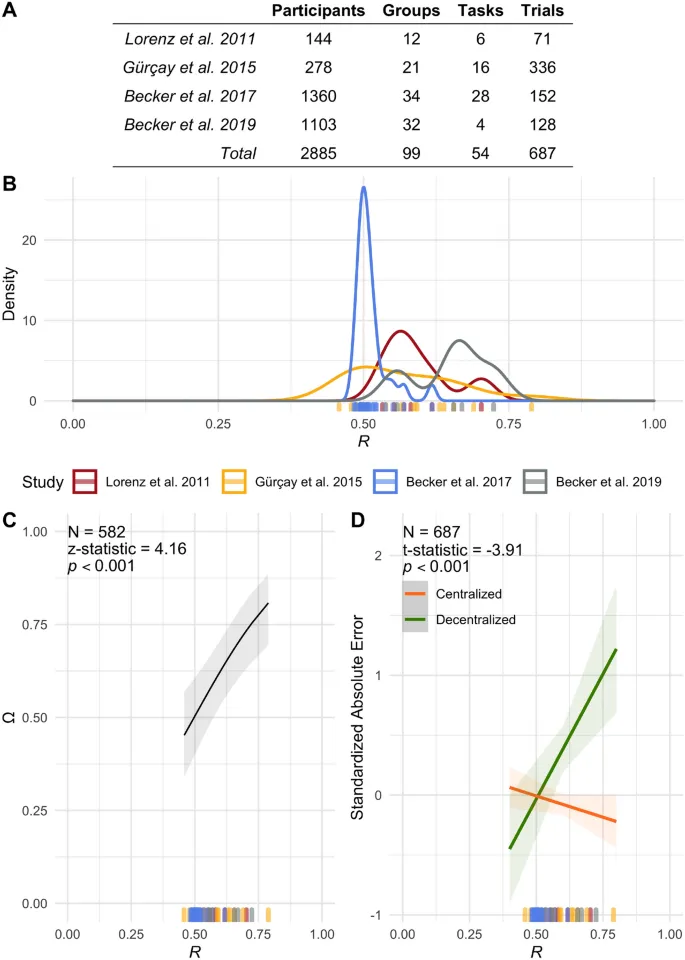
Чтобы эмпирически проверить предсказания вышеупомянутой модели, мы используем данные, относящиеся к задачам положительной числовой оценки (т.е. задачи с пропущенными отрицательными оценками), из четырех опубликованных лабораторных экспериментов с участием людей^9,10,14,16. В этих экспериментах в общей сложности 2885 участников, организованных в 99 независимых групп, выполнили в общей сложности 54 задачи оценки, сгенерировав в общей сложности 15 562 индивидуальные оценки и 687 коллективных оценок (см. Рисунок 3A).

Все четыре эксперимента следовали схожей процедуре, включавшей три этапа:

1. Участники одновременно и независимо выполняли задачи числовой оценки по ряду тем, таких как визуальная оценка, вопросы на общие знания, политические факты и экономические прогнозы;
2. Внутри групп разного размера участники в условиях социального взаимодействия обменивались информацией о своих оценках;
3. Участники имели одну или несколько возможностей пересмотреть свои оценки.

Один испытание состояло из одной группы участников, отвечающих на один вопрос.

Каждая задача вызывает разное распределение начальных оценок, наблюдаемых эмпирически. Для каждой задачи мы используем относительную логарифмическую вероятность (log likelihood) между подогнанным лог-нормальным распределением и нормальным распределением (далее обозначается как R) в качестве меры тяжести хвоста распределения начальных оценок. Другими словами, эта мера отражает, лучше ли начальные оценки для данной задачи описываются распределением с тонкими хвостами (т.е. нормальным распределением) или с тяжелыми хвостами (т.е. лог-нормальным распределением). R=0 с 100% уверенностью указывает, что начальные оценки лучше подходят для нормального распределения, чем для лог-нормального; R=1 с 100% уверенностью указывает, что начальные оценки лучше подходят для лог-нормального распределения, чем для нормального; R=0.5 указывает, что начальные оценки могут быть одинаково описаны как нормально, так и лог-нормально. Рисунок 3B показывает распределение эмпирически полученных R в этих исследованиях, что подтверждает, что большинство эмпирических распределений начальных оценок лучше описываются распределением с тяжелыми хвостами, чем с тонкими.

Мы называем среднюю оценку индивидов в каждой группе до и после их взаимодействия их коллективной начальной и пересмотренной оценкой соответственно. Для каждого испытания мы сравниваем абсолютные ошибки коллективных начальных и пересмотренных оценок, используя следующие два метрика исхода:

1. Улучшилась ли коллективная пересмотренная оценка по сравнению с коллективной начальной оценкой в группах с социальным взаимодействием;
2. Стандартизированная (z-оценка) абсолютная ошибка пересмотренной коллективной оценки для всех групп (с социальным взаимодействием или без него).

Мы используем логистическую регрессию для первого и линейную регрессию для второго.

Этот эмпирический анализ основан на следующем предположении: коллективная начальная оценка соответствует наиболее децентрализованной структуре влияния (mega =0), а социальные взаимодействия могут только увеличить централизацию влияния (mega >0). Например, даже в условиях социального взаимодействия, где все равноправно связаны с точки зрения структуры коммуникации, некоторые члены группы могут стать более влиятельными, чем другие, благодаря своей разговорчивости³¹, убедительности или устойчивости к социальному влиянию^10,17. Ключевая идея заключается в том, что коллективная начальная оценка (до социального взаимодействия) исключает возможность какого-либо изменения влияния и поэтому эквивалентна наиболее децентрализованной сети. В отличие от этого, коллективная пересмотренная оценка (после социального взаимодействия) может быть непропорционально подвержена влиянию доминирующих индивидов и, следовательно, может быть смоделирована как централизованная сеть влияния. Эта же идея может быть распространена на моделирование неструктурированного обсуждения как централизованного влияния, а метода Дельфи (и других методов опосредованной коммуникации) как относительно децентрализованных сетей. (Заинтересованному читателю может быть предложено более подробное обсуждение в последующей работе Беккера и др.³², показывающей применение этого модельного подхода и наших результатов здесь для объяснения, почему неструктурированное обсуждение иногда превосходит числовую коммуникацию, а иногда результат меняется на противоположный).

Здесь мы начинаем с использования смешанной модели (см. SI Секцию S3.1 для спецификации) для проверки основной гипотезы, предсказанной нашей теорией, а именно, что эффект централизации социального влияния на производительность групп модерируется нашей мерой тяжести хвоста распределения начальных оценок, R. Как показано на Рисунке 3C, мы обнаруживаем, что вероятность того, что группа улучшит свои результаты после централизованного социального взаимодействия — обозначаемая как mega как интересующая нас переменная исхода — существенно объясняется R (z-статистика =4.16; p<0.001). В частности, когда R высока, группы с большей вероятностью улучшают свои результаты благодаря централизованному социальному взаимодействию. С другой стороны, когда R низка, группы с меньшей вероятностью улучшают свои результаты благодаря централизованному социальному взаимодействию. И наоборот, когда R низка (особенно когда R < 0.5), средняя абсолютная ошибка пересмотренной коллективной оценки ниже в централизованных структурах (Рисунок 3D).

Обсуждение

Основной вклад этой статьи заключается в примирении предыдущих исследований по фундаментальному вопросу понимания производительности групп: как социальное влияние влияет на точность коллективных оценок? Критическое следствие наших результатов заключается в том, что атрибуты распределения начальных оценок (т.е. контекст оценки) модерируют эффект централизации влияния. Следовательно, мы не находим подтверждения гипотезе о том, что децентрализованные структуры влияния предпочтительнее централизованных независимо от контекста оценки.

Таким образом, эффект структуры сети на производительность коллективной оценки следует переосмысливать в контекстно-зависимой системе, которая учитывает популяцию индивидов, выполняющих конкретную задачу. Не существует единой структуры влияния, которая была бы лучше других во всех контекстах. Такая контекстно-зависимая система может объединить ранее противоречивые выводы о "мудрости толпы" в рамках единой теоретической системы и объяснить эффекты структуры сети влияния на качество коллективных оценок.

Признаем, что контекст оценки является лишь одним из нескольких потенциальных источников несоответствий в предыдущих исследованиях. Например, расплывчатость или двусмысленность некоторых теоретических конструктов, таких как влияние, может привести к тому, что различные исследования одного и того же явления будут измерять разные вещи.

Хотя расчет предложенной нами характеристики контекста оценки, R, не требует знания истины (оцениваемого), он требует доступа к набору начальных оценок группы. Однако мы отмечаем, что исследования простых задач оценки показали, что аналогичные классы задач оценки имеют тенденцию давать схожие и надежно предсказуемые распределения начальных оценок²⁰. Таким образом, в качестве рекомендации, для группы, которая регулярно нуждается в выполнении одного и того же класса задач оценки, может быть возможно калибровать структуру группы на основе исторических данных и долгосрочной обратной связи.

Более того, производительность структур влияния может значительно варьироваться в зависимости от выбранной функции потерь. В этой статье наша функция потерь определяется как вероятность того, что коллективная оценка, сгенерированная централизованной структурой влияния, ближе к истине, чем оценка, сгенерированная децентрализованной структурой. Однако выбор функции потерь обычно зависит от конкретного приложения. См. Рисунок S4 для примеров других функций потерь.

Наконец, отметим, что мы изучали только один класс задач: числовая оценка с неотрицательной, объективной истиной. Соответствующие исследования других классов задач также продемонстрировали, что вариации контекстуальных характеристик, таких как сложность^{33,34,35,36,37,38}, фундаментально изменяют исходы коллективного решения проблем. Также стоит отметить наше внимание к задачам, связанным с социальным влиянием, в то время как в реальности мы не должны исключать возможность того, что простое агрегирование предварительных оценок индивидов может быть подходящим, бесплатным решением для некоторых ситуаций. Однако такие ситуации выходят за рамки настоящего исследования, и мы отсылаем заинтересованного читателя к обширной существующей литературе по правилам агрегирования (например,^39,40,41).

В заключение, наш теоретический и эмпирический анализ продемонстрировал, что выводы о роли социального влияния могут быть непоследовательными, если контекст оценки явно не учитывается. Из этой системы вытекает множество направлений для дальнейших исследований. Например, в отличие от того, что предполагается в большинстве доступных работ, включая нашу, социальные сети, в которых мы живем, не являются случайными, и они не навязываются внешними силами. Скорее, эти социальные сети возникают под влиянием эндогенных социальных процессов и постепенно развиваются в потенциально нестационарном контексте. Важным направлением будущих исследований является изучение последствий коррелированного размещения индивидов, при котором более точные индивиды с большей или меньшей вероятностью занимают более влиятельные позиции. Мы ожидаем, что по мере увеличения степени этой корреляции преимущества или вред централизации станут выраженными и будут более последовательно проявляться в более широком диапазоне задач и контекстуальных характеристик. Истинный контекстно-зависимый взгляд на "мудрость толпы" должен открыть связи с различными областями исследований и помочь продвинуть междисциплинарное понимание проектирования социальных систем и их информационных исходов.

Материалы и методы

Теоретический анализ mega

Мы измеряем вероятность того, что коллективная оценка, полученная централизованной структурой влияния, {{athbf {a}}}^{n}(mega ), mega > 0, превосходит децентрализованную базовую линию, {{athbf {a}}}^{n}(0). Мы обозначаем эту вероятность как mega _n(mega ,{athcal {F}}^{ heta }_{u ,igma }) := {athbb {P}}^{ heta }_{u ,igma }[|{{athbf {a}}}^{n}(mega ) - heta | < |{{athbf {a}}}^{n}(0) - heta |]. Для mega n [0,1) мы можем показать, что mega _n(mega ,{athcal {F}}^{ heta }_{u ,igma }) > 1/2 если и только если athbb {E}[({{athbf {a}}}_{1,0} - heta ) id ext{Agent 1 is central}] > 0. Мы также вычисляем нижнюю границу для mega _n:

$$ mega _n(mega ,{athcal {F}}^{ heta }_{u ,igma }) e rac{1}{1+xp ( au _n (1mega )/mega )}, $$

где au _n = rac{1}{n}um _{i=1}^n og rac{1-F^{ heta }_{u ,igma }(a_{i,0})}{F^{ heta }_{u ,igma }(a_{i,0})}, и F^{ heta }_{u ,igma } — кумулятивная функция распределения начальных оценок. В SI Секции S2.1 мы показываем, как ограничение скорости затухания хвоста для различных классов распределений дает нетривиальную (ненулевую) нижнюю границу при n ightarrow nfty. Для распределений с тяжелыми хвостами, таких как Парето, лог-Лапласа и лог-нормальное (см. SI Секции S2.1.1–S2.1.3), мы выявляем фазовые переходы, когда предлагаемая нижняя граница переходит от 0 к 1 или 1/2, когда igma пересекает критическое значение.

Статистические тесты

Все статистики были двусторонними и основаны на смешанных моделях, которые включали случайные эффекты по группам и по исследованиям (т.е. четыре лабораторных эксперимента с участием людей, которые мы повторно проанализировали^9,10,14,16) для учета вложенной структуры данных. В частности, логистическая регрессия для Рисунка 3C имеет вид:

$$ y_{ij} = rac{1}{1+xp (b_0 + b_1 R_{j} + v_i + u_i + psilon _{ij})}, $$

где y_{ij} — бинарный индикатор того, улучшила ли i-я группа в j-м контексте оценки точность своей коллективной оценки после социального взаимодействия; b_0 — фиксированный перехват для регрессионной модели; b_1 — фиксированный коэффициент для характеристики контекста оценки, R; v_i — случайный коэффициент для i-й группы; u_i — случайный коэффициент для исследования, к которому принадлежит i-я группа; и psilon _{ij} — член гауссовской ошибки. Анализ проводился на 678 наблюдениях (группы с социальным влиянием).

Уравнение регрессии для Рисунка 3D имеет вид:

$$ y_{ij} = b_0 + b_1 R_{j} + b_2 I_{i} + b_3 I_{i} R_{j} + v_i + u_i + psilon _{ij}, $$

где y_{ij} — стандартизированная (z-оценка) абсолютная ошибка пересмотренной коллективной оценки для i-й группы в j-м контексте оценки, R_{j}; b_0 — фиксированный перехват для регрессионной модели; b_1 — фиксированный коэффициент для характеристики контекста оценки, R; I_{i} n 0,1 — индикаторная переменная, показывающая, произошло ли социальное взаимодействие; b_2 — фиксированный коэффициент для централизации социального влияния; b_3 — фиксированный коэффициент для взаимодействия между характеристикой контекста оценки, R, и централизацией влияния (показано на Рисунке 3D); v_i — случайный коэффициент для i-й группы; u_i — случайный коэффициент для исследования, к которому принадлежит i-я группа; и psilon _{ij} — член гауссовской ошибки. Абсолютная ошибка пересмотренной коллективной оценки была стандартизирована (z-оценкой) для сравнения ошибок по различным задачам (правильный ответ для разных задач может отличаться на порядки). Анализ проводился на 687 наблюдениях; 582 группы с социальным влиянием (централизованные) и 105 групп без социального влияния (децентрализованные). Дальнейшие детали регрессионного анализа приведены в SI Секции S3.1 и Таблице S1. Проверки робастности регрессионных результатов представлены в Таблицах S2 и S3.