Менделевская рандомизация: выявление причинно-следственных связей в генетических исследованиях

Введение

Одной из давних проблем в эпидемиологии является выявление причинно-следственных связей на основе корреляционных данных, полученных в наблюдательных исследованиях. Корреляционные исследования служат отправной точкой для изучения причинно-следственных связей между переменными. Однако сами по себе корреляции недостаточны для установления причинности из-за потенциального наличия фоновых конфаундер-факторов (смешивающих переменных) и неопределенности направления причинно-следственной связи.

Основной альтернативой наблюдательным исследованиям являются рандомизированные контролируемые испытания (РКИ), в которых участники исследования случайным образом распределяются в экспериментальную (группа лечения) и контрольную группы. Этот подход в среднем одинаково распределяет эффекты любых конфаундер-факторов между группами, так что любое различие в исходе может быть отнесено на счет вмешательства. Однако РКИ не всегда осуществимы. Трудности могут возникнуть из-за этических соображений, например, в исследованиях с участием детей.

Менделевская рандомизация (МР)

Менделевская рандомизация (МР) может быть использована для исследования причинно-следственных связей в случаях, когда РКИ неосуществимы или неэтичны. МР основана на законах Менделя о сегрегации и независимом наследовании признаков, используя рандомизацию, которая происходит во время мейоза (когда генетическая информация перемешивается между хромосомами, а затем эти хромосомы формируют гаметы), как квазиэкспериментальную манипуляцию (Madole and Harden 2022). Генетические ассоциации с фенотипическими экспозициями (воздействиями), выявленные в крупномасштабных полногеномных ассоциативных исследованиях (GWAS - Genome-Wide Association Studies) и мета-анализах, или их взвешенные комбинации, являются потенциально полезными инструментальными переменными (Evans and Davey Smith 2015; Sanderson et al. 2022).

Ключевые предпосылки МР

Для выявления причинно-следственных связей на основе МР задействовано несколько ключевых предпосылок (Sanderson et al. 2022):

• Предпосылка релевантности (Relevance Assumption): Связь между генетическим вариан(ами) и экспозицией должна быть сильной (обычно определяется F-статистикой, превышающей 10).
• Предпосылка обмениваемости (Exchangeability Assumption): Генетический вариант не должен быть связан с конфаундер-фактором в соотношении между экспозицией и исходом.
• Предпосылка эквивалентности ген-среда (Gene-Environment Equivalence): Воздействие изменения генетической предрасположенности на переменную экспозиции такое же, как и воздействие эквивалентного по величине изменения средового фактора, то есть оба вызывают одинаковое изменение в выходной переменной. Эта предпосылка подчеркивает, что, в отличие от близнецовых дизайнов, в стандартной МР данных неродственных индивидов нет разделения аддитивных генетических, общих и средовых вариаций.
• Предпосылка исключения (Exclusion Restriction Assumption): Связь инструмента (генетического варианта) с исходом полностью опосредована экспозицией. В генетических исследованиях эта предпосылка известна как отсутствие горизонтального плеотропизма. Это предположение вряд ли будет выполняться для сложных признаков, учитывая, что GWAS показали, что один и тот же вариант часто влияет на несколько признаков. Горизонтальный плеотропизм возникает, когда инструмент влияет на исход через пути, отличные от экспозиции.

Решения для проблемы горизонтального плеотропизма

Для обнаружения и/или учета горизонтального плеотропизма в причинно-следственных выводах на основе МР было предложено несколько решений (Sanderson et al. 2022):

• Использование методов, которые ослабляют это предположение и требуют только, чтобы сила инструмента была независима от прямого эффекта экспозиции на исход (Bowden et al. 2015).
• Триангуляция результатов из различных МР-методов для подтверждения согласованности силы и направления причинного сигнала между тестами (Burgess et al. 2011).
• Разработка оценщиков, основанных на моде (mode) (Hartwig et al. 2017) и взвешенной медиане (weighted median) (Bowden et al. 2015) оценок размера эффекта инструмента, для решения проблемы горизонтального плеотропизма.

Расширенные модели МР

Альтернативные методы, интегрирующие МР в близнецовый дизайн, были предложены для решения проблемы предпосылки исключения (Hwang et al. 2021). К ним относятся:

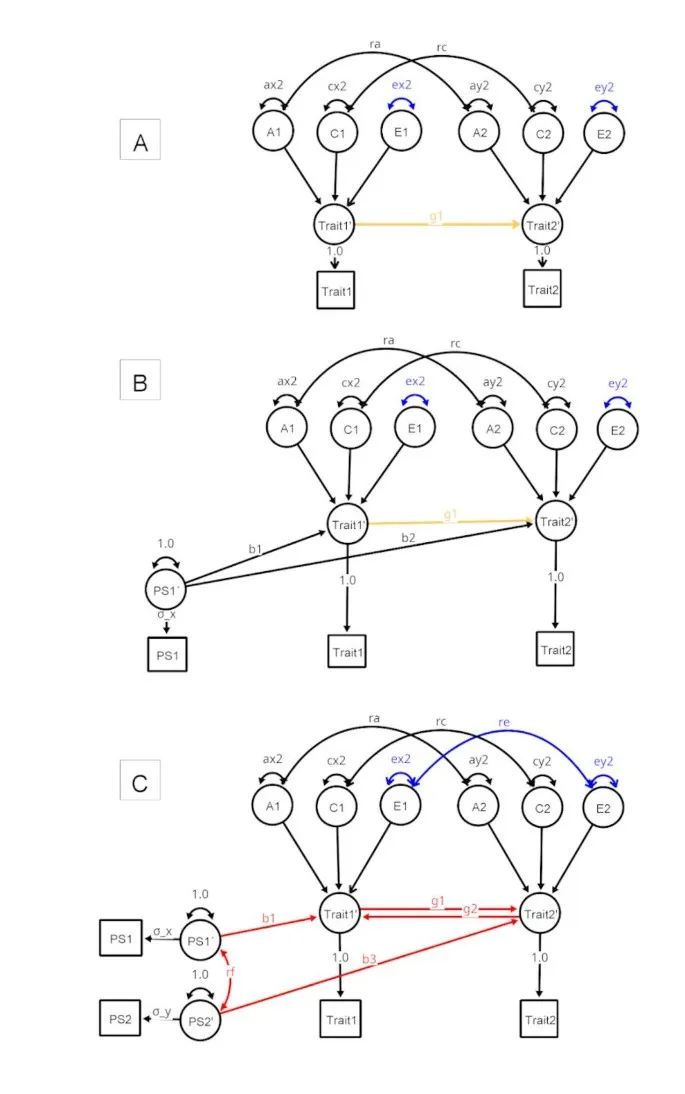
• MRDoC (Minică et al. 2018): Эта модель комбинирует МР с близнецовым дизайном "Направление причинности" (DoC - Direction of Causation, Fig. 1). Модель MRDoC включает (горизонтальный) плеотропный путь, учитывающий прямую связь между инструментальной переменной и исходом, что позволяет тестировать направленный горизонтальный плеотропизм (путь b2, Рис. 1B). Требованием для оценки b2 в MRDoC является необходимость фиксации re (корреляция уникальной среды) на ноль для идентификации модели.
• MRDoC2 (CastrodeAraujo et al. 2023): Эта модель является расширением MRDoC для учета двунаправленной причинности при наличии фонового конфаундинга. Она включает полигенный скор (PRS - Polygenic Score), который действует как инструментальная переменная для исхода. Модель позволяет оценивать эффекты обратной причинности (пути g2, Рис. 1C).

Далее мы будем ссылаться на модель Minică et al. (2018) как MRDoC, а на модель CastrodeAraujo et al. (2023) как MRDoC2. Список параметров для каждой модели приведен в Таблице 1.

Таблица 1. Параметры в трех факториальных дизайнах, с соответствующим общим количеством ячеек для каждого дизайна симуляции.

Рис. 1. Спецификации моделей DoC (A), MRDoC (B) и MRDoC2 (C) для одного члена пары близнецов.

Модели включают эффекты аддитивных генетических (A), общих средовых (C) и уникальных средовых (E) факторов для обоих признаков (Trait 1 и Trait 2), и их эффекты могут коррелировать между признаками (параметры ra, rc, и re). Генетические ковариации между близнецами умножаются на 1 для однояйцевых (MZ - Monozygotic) и на 0.5 для двуяйцевых (DZ - Dizygotic), а ковариации общей среды между близнецами умножаются на 1 как для MZ, так и для DZ. Метки путей красным цветом важны для мощности модели, синим - подвержены ошибкам измерения, оранжевым - подвержены ошибкам измерения и важны для мощности модели. Латентные переменные Trait1' и Trait2' не требуются для идентификации, но сохранены для соответствия статье CastrodeAraujo et al. (2023), чтобы подчеркнуть решение масштабирования PS1' и PS2' и указать, что возможным расширением этих моделей является использование множественных индикаторов. Модели оценивались с использованием компонентов дисперсии; ra, rc, и re оценивались наряду с ковариациями (цветное изображение онлайн).

Ограничения модели DoC

Модель DoC использует перекрестные корреляции между близнецами и признаками для извлечения информации о возможных причинных путях между двумя фенотипами. Однако она имеет следующие ограничения:

• Различия в надежности переменных: Различия в надежности переменных в модели могут исказить оценки причинно-следственных связей (Heath et al. 1993; Gillespie et al. 2003). В частности, более надежная переменная с большей вероятностью будет идентифицирована как причина менее надежной переменной (Heath et al. 1993; Duffy and Martin 1994).
• Предпосылка об отсутствии корреляции уникальной среды (re=0): Как DoC, так и MRDoC требуют предположения, что корреляция уникальной среды (параметр re на Рис. 1C) равна нулю для оценки причинного пути между экспозицией и исходом. Это ограничение подразумевает, что уникальные средовые воздействия не являются источником конфаундинга. Нарушение этого предположения искажает причинные оценки в моделях DoC (Rasmussen et al. 2019), но не является проблемой для MRDoC2, которая явно моделирует этот тип конфаундинга. Для MRDoC неясно, насколько искажение при некорректном предположении re ≠ 0 повлияет на оценки интереса, в частности, на причинный путь (g1) или другие пути (Рис. 1B).

Сравнение статистической мощности моделей

Статистическая мощность моделей MRDoC и MRDoC2 была исследована в работах Minică et al. (2018) и CastrodeAraujo et al. (2023) соответственно. Однако сравнение профилей мощности всех трех моделей (DoC, MRDoc и MRDoc2) отсутствует. Хотя все три модели фокусируются на причинно-следственных выводах, они различаются по своим предпосылкам:

• Модель DoC: Может учитывать как однонаправленную, так и двунаправленную причинность, при условии, что некоторые другие параметры фиксированы. То есть, помимо двух причинных путей, может быть совместно оценена только одна из трех возможных причин (A, C, E) конфаундинга. Это означает, что из трех корреляций (ra, rc, re) две должны быть ограничены (обычно до нуля или до другого значения в зависимости от гипотез). В общем случае, бивариантная ACE-модель идентифицируется при свободном оценивании любых трех из пяти возможных коэффициентов пути, моделирующих ковариацию между двумя фенотипами (параметры ra, rc, re, g1 и g2; Рис. 1) (Maes et al. 2021).
• Модель MRDoC: Обычно специфицируется с однонаправленной причинностью (поскольку двунаправленная причинность требует дополнительных ограничений для фонового ACE-конфаундинга) и предполагает отсутствие конфаундинга уникальной средой (re = 0, Рис. 1).
• Модель MRDoC2: Является двунаправленной и предполагает отсутствие прямого горизонтального плеотропизма (путь b2 в MRDoC фиксирован на ноль в MRDoC2). Однако MRDoC2 учитывает два источника косвенного горизонтального плеотропизма (rf*b1 и rf*b3 на Рис. 1C), позволяя инструментам быть коррелированными через rf. Она также включает вертикальный плеотропизм через причинные эффекты на экспозицию.

В данной статье мы сравнили профили статистической мощности трех моделей. Мы оценили эффекты фенотипической ошибки измерения и уникального средового конфаундинга в DoC и MRDoC (re ≠ 0). В конечном итоге мы определили ситуации, в которых каждая модель работает оптимально с точки зрения мощности.

Структура статьи:

1. Спецификации моделей.
2. Дизайны симуляций.
3. Тестирование смещения из-за ошибки измерения путем введения ненадежных фенотипов.
4. Представление результатов симуляций, в которых уникальный средовой конфаундинг (re на Рис. 1) был зафиксирован на ноль, тогда как в процессе генерации данных он присутствовал.
5. Отчет о статистической мощности трех моделей.

Методы

Спецификация моделей

Спецификации трех моделей были представлены в оригинальных публикациях: DoC (Heath et al. 1993; Neale and Cardon 1992), MRDoC (Minică et al. 2018) и MRDoC2 (CastrodeAraujo et al. 2023). Все три модели разделяют классическую близнецовую декомпозицию дисперсии на аддитивные генетические (A), общие средовые (C) и уникальные средовые (E) компоненты (Рис. 1). Модели являются бивариантными: Trait1 и Trait2 - это фенотипы, и они специфицированы таким образом, что между двумя признаками могут существовать ноль, один или два причинных пути (g1 или g2, или оба). Классическая модель близнецов представлена на Панели A Рис. 1, известная как модель "Направление причинности" (Direction of Causation), которая вложена как в MRDoC, так и в MRDoC2. Спецификация тестируемой модели DoC включает ковариацию/конфаундинг из-за аддитивных генетических факторов (ra) и общих средовых факторов (rc). MRDoC не вложена в MRDoC2 из-за наличия ограничений, необходимых для идентификации (наличие прямых путей горизонтального плеотропизма от PS1 к Trait 2' в MRDoC). Эти модели были специфицированы в коде OpenMx с использованием матричной алгебры и подхода компонентов дисперсии (Verhulst et al. 2019). Следует отметить, что в предыдущих работах модели были специфицированы с использованием коэффициентов пути (Minică et al. 2018; CastrodeAraujo et al. 2023). Примечательно, что в настоящей спецификации оцениваются дисперсии, а пути фиксированы, тогда как в предыдущих спецификациях дисперсии были фиксированы, а пути оценивались. В этой версии дисперсии могут быть отрицательными, что, как известно, приводит к лучшей калибровке уровней ошибки I рода (Verhulst et al. 2019). Однако корреляции ra, rc и re оцениваются, и эти корреляции приведены на диаграмме и во всех графиках. Этот подход соответствует недавним работам нашей группы (Maes et al. 2022; CastrodeAraujo et al. 2024). Код для каждой модели общедоступен в виде функции в пакете umx R (Bates et al. 2019).

Дизайны симуляций

Мы провели симуляционные исследования для сравнения моделей DoC, MRDoC и MRDoC2, а также для изучения известных ограничений близнецовых моделей DoC и MRDoC. Мы рассмотрели три проблемы: влияние ненадежности фенотипических измерений на оценки параметров; влияние мисспецификации моделей относительно параметра re (некорректно зафиксирован re=0); и мощность, путем оценки ассоциаций между параметрами моделей и параметром нецентральности в тестах нулевых гипотез в каждой модели.

Мы использовали точную симуляцию данных для генерации исходных данных на основе матрицы ковариаций популяции. Используя этот метод, мы гарантируем, что матрица ковариаций сгенерированных исходных данных точно соответствует матрице ковариаций популяции. Это равенство означает, что при подгонке истинной модели (при условии ее идентификации) оценки параметров точно соответствуют значениям популяции. Следовательно, тест гипотезы, основанный на тесте отношения правдоподобия (например, фиксация параметра на ноль), может рассматриваться как параметр нецентральности, который мы можем использовать в расчетах мощности (van der Sluis et al. 2008). Метод состоит из следующих пяти шагов:

1. Выбор значений параметров интересующей модели.
2. Симуляция многомерно нормально распределенных исходных данных на основе ожидаемых матриц ковариаций и средних значений однояйцевых (MZ) и двуяйцевых (DZ) близнецов. Для этого мы использовали функцию mvrnorm() из библиотеки R MASS с размерами выборок MZ и DZ по 1000 пар (Venables et al. 2002). Опция empirical=TRUE использовалась для удаления вариации выборки в средних, дисперсиях и ковариациях симулированных выборок.
3. Подгонка истинной модели с использованием максимального правдоподобия, таким образом восстанавливая истинные значения параметров.
4. Подгонка ложной модели путем наложения интересующего ограничения(ий) (например, фиксация параметра на ноль).
5. Извлечение параметра нецентральности (NCP - Noncentrality Parameter), который равен разнице между минус удвоенным логарифмом правдоподобия моделей, подогнанных на шагах 3 и 4, и его использование для расчета мощности отвергнуть интересующий параметр при уровне ошибки I рода 0.05.
6. Смещение получается путем вычитания среднего истинного значения в факторе из среднего оцененного значения параметра, затем отображается на гистограммах.

Далее мы представляем в общей сложности пять симуляций с комбинацией факториальных дизайнов и процессов генерации данных. Дизайны перечислены в Таблице 1, где параметры представлены как факторы дизайна, а их значения - как уровни факторов. Выбранные значения были сопоставимы со значениями, использованными в предыдущей публикации (CastrodeAraujo et al. 2023), в которой предпринималась попытка моделировать фенотипы с наследуемостью от 0.3 до 0.5 и сильными инструментами (b1 и b3) от 0.16 до 0.20. Все дизайны симуляций включали многомерные модели с дисперсиями A, C и E. В интересах краткости, уровни факторов (значения параметров) были одинаковыми во всех дизайнах. Хотя использовалась спецификация типа компонентов дисперсии, мы рассчитывали корреляции ra, rc и re с помощью матричной алгебры, чтобы избежать смешивания компонент ковариации и корреляций. Наконец, количество параметров в каждом дизайне зависит от количества параметров в каждой из моделей (DoC, MRDoC и MRDoC2), таким образом, Дизайн 1 имеет 9 параметров (g1, ax2, cx2, ex2, ay2, cy2, ey2, ra, и rc); Дизайн 2 - 11 параметров (g1, b1, b2, ax2, cx2, ex2, ay2, cy2, ey2, ra, и rc); Дизайн 3 - 14 параметров (g1, g2, b1, b3, rf, ax2, cx2, ex2, ay2, cy2, ey2, ra, rc, и rc).

В первом наборе симуляций модели подгонялись к данным, сгенерированным по тому же дизайну, то есть Дизайн 1 для DoC, Дизайн 2 для MRDoC и Дизайн 3 для MRDoC2. Симуляции 1 и 2 были разработаны для оценки влияния ненадежных фенотипов и влияния конфаундинга уникальной средой на смещение для всех трех моделей (Таблица 1, Дизайны 1, 2 и 3). Следующий набор симуляций подгонял каждую модель к данным, сгенерированным точно в соответствии с матрицей ковариаций MRDoC2, полученной из значений параметров в Таблице 1, Дизайн 3. Обоснованием генерации данных по более сложной модели было облегчение сравнений между тремя моделями с использованием наименее ограничительной (и, возможно, наиболее реалистичной) модели для генерации данных. Симуляции 1 и 2 были повторены с новым процессом генерации данных. Финальная симуляция оценила мощность трех моделей для отвержения гипотезы о том, что причинный параметр равен нулю.

Симуляция 1: Ненадежные фенотипы

Сначала мы оценили влияние ненадежности в фенотипических измерениях на оценки параметров. Надежность фенотипов была установлена так, чтобы отразить известный недостаток модели DoC, в которой более надежный фенотип с большей вероятностью будет идентифицирован как причина менее надежного фенотипа, поэтому надежность экспозиции была установлена на уровне 0.90, а надежность исхода - на уровне 0.70. Это было сделано путем спецификации члена ошибки измерения на фенотипическом уровне со значениями, зафиксированными на уровне 0.1 и 0.3 для Trait 1 и Trait 2 соответственно. Ошибка измерения была смоделирована так, чтобы она не входила в передаваемую дисперсию между двумя признаками. По сути, экспозиция и фенотипы исхода были заменены латентными переменными, между которыми моделировалась причинность. Латентные переменные вызывали соответствующие наблюдаемые переменные с коэффициентом регрессии, равным квадратному корню из надежности. Наблюдаемые переменные имели остаточную дисперсию, установленную как единица минус надежность. Эта новая структура ковариаций затем использовалась как данные для подгонки моделей. Смещение, обусловленное ненадежностью, было рассчитано как средняя разница между истинными значениями параметров и оценками параметров, усредненными по симуляциям точных данных (Рис. 2A).

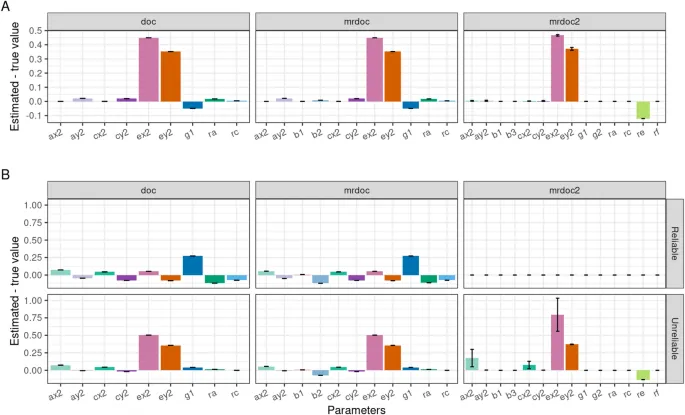
Рис. 2. Результаты симуляции оценки смещения из-за ошибки измерения в DoC, MRDoC и MRDoC2. Для каждого оцененного параметра на оси X plotted средняя разница между истинными значениями параметров и оценками параметров в симуляциях точных данных. Надежность была установлена на уровне 90% для экспозиции (Trait 1) и 70% для исхода (Trait 2) в симуляции точных данных (Дизайны 1, 2 и 3; Таблица 1). A - Симуляция при подгонке моделей к данным, сгенерированным с помощью тестируемой модели. B - Процесс генерации данных - MRDoC2.

Результаты

Смещение из-за ошибки измерения

Для оценки влияния ошибки измерения фенотипов мы ввели ненадежность как для экспозиции (10%; т.е. надежность 0.9), так и для исхода (30%; т.е. надежность 0.7). Результаты, полученные в симуляциях, показаны на Рис. 2. В DoC и MRDoC причинный путь (g1) был недооценен при ненадежных измерениях фенотипов, в то время как оценки уникальной среды были смещены в сторону завышения, пропорционально степени ненадежности (Рис. 2A). Ошибка измерения не повлияла на оценки причинного пути (g1, g2) в MRDoC2. Следовательно, MRDoC2 была более устойчивой, чем MRDoC, когда доля ошибки измерения отличалась между фенотипами.

Когда данные генерировались с использованием модели MRDoC2 (Рис. 2B), мы обнаружили схожие уровни смещения в DoC и MRDoC. Отсутствие путей из MRDoC2 в MRDoC (re, rf, b3) и DoC (b1, b2) привело к повсеместному смещению оценок моделей с заметным завышением g1 с ошибкой измерения или без нее. Оценки уникальной средовой дисперсии были смещены в сторону завышения при наличии ошибки измерения (ненадежных фенотипов).

Смещение из-за средового конфаундинга

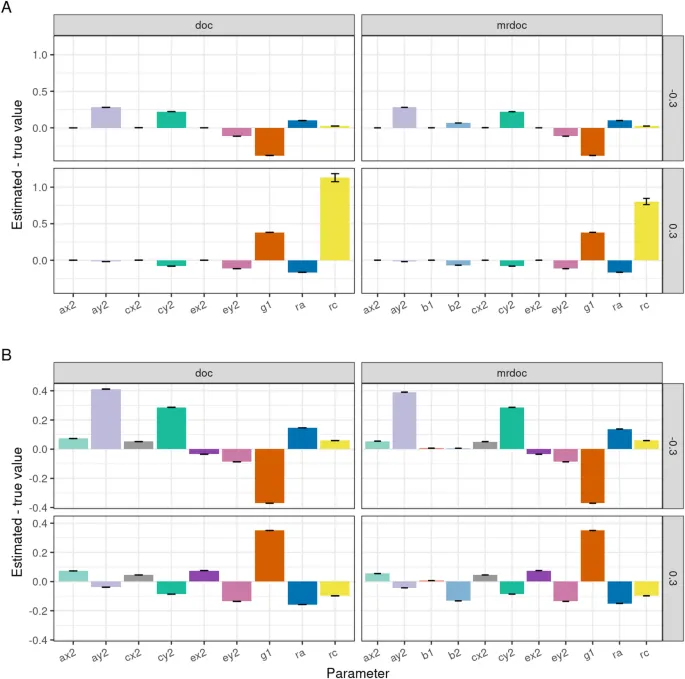
Результаты симуляции влияния мисспецификации уникального средового конфаундинга (re) представлены на Рис. 3A, B. Если re было истинно положительным (+ 0.3), спецификация re=0 привела к завышению причинного параметра g1 как в DoC, так и в MRDoC (Рис. 3A, нижняя грань). И наоборот, g1 был недооценен, когда re было истинно отрицательным (− 0.3), но предполагалось равным нулю (Рис. 3A, верхняя грань). Таким образом, когда модели DoC и MRDoC подгонялись к данным, сгенерированным MRDoC2, смещение в оценках параметров было повсеместным (Рис. 3B). В отличие от этого, причинные (g1, g2) и плеотропные (b1, b3) пути оставались несмещенными в симуляции MRDoC2 (не показано).

Рис. 3. Результаты симуляции оценки смещения из-за мисспецификации параметра уникального средового конфаундинга (re). A относится к симуляциям, когда модели подгонялись к данным, сгенерированным с помощью тестируемой модели. B относится к симуляциям с использованием MRDoC2 в качестве процесса генерации данных (Дизайн 3, Таблица 1). Верхние грани: точная генерация данных re = + 0.3. Нижние грани: точная генерация данных для re = − 0.3. MRDoC2 не показала смещения в этих тестах.

Влияние каждого параметра модели на мощность

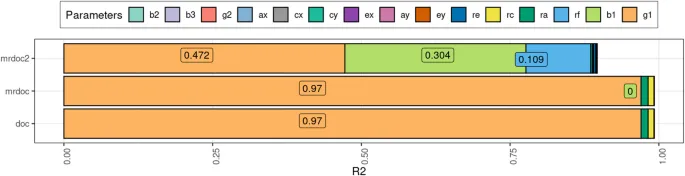
Мы сравнили профили статистической мощности каждой модели. Для этого шага модели подгонялись к данным, сгенерированным с помощью тестируемой модели, т.е. Дизайн 1 для DoC, Дизайн 2 для MRDoC и Дизайн 3 для MRDoC2. MRDoC2 является двунаправленной моделью, но здесь мы сосредоточились только на мощности для отвержения гипотезы g1 = 0 при уровне альфа 0.05. Данные были стандартизированы с помощью cov2cor() в ожидаемой матрице ковариаций для MZ и DZ перед оценкой. NCP (параметры нецентральности) из этого теста мощности были регрессированы на значения параметров, а коэффициенты каждой регрессии были представлены в виде столбчатой диаграммы на Рис. 4. Общее R2, доля дисперсии NCP, объясняемая параметрами, составила 0.99 в модели DoC, 0.99 в модели MRDoC и 0.90 в модели MRDoC2. Чем длиннее столбцы данного параметра, тем больше дисперсии NCP объясняет параметр. Мы обнаружили, что g1 оказывал наибольшее влияние на мощность DoC и MRDoC для обнаружения g1, а b1 и rf также оказывали большое влияние на мощность MRDoC2. Кроме того, ra и rc оказывали небольшое, но заметное влияние на мощность в моделях DoC и MRDoC. Обратите внимание, что в MRDoC путь от инструмента к экспозиции (b1) не вносил вклада в мощность модели. Это означает, что дисперсия, объясняемая инструментом, не влияет на мощность отвержения гипотезы g1 = 0 на 0.05 уровне значимости в MRDoC. Кроме того, все проведенные тесты мощности были тестами гипотезы g1 = 0, чтобы сделать результаты более сопоставимыми между моделями. Однако в MRDoC2 также возможно провести 2df тест мощности, опуская как g1, так и g2.

Рис. 4. Результаты симуляции оценки статистической мощности DoC, MRDoC и MRDoC2 для отвержения гипотезы g1 = 0. Данные были стандартизированы. Штабелированные столбцы представляют собой коэффициенты регрессии параметра нецентральности (NCP) как функции значений параметров модели. Общее R2 для модели DoC составило 0.99, для MRDoC - 0.99, для MRDoC2 - 0.90.

Обсуждение

Мы представили серию симуляций, посвященных вопросам: (1) ошибки измерения, (2) мисспецификации конфаундинга уникальной средой и (3) статистической мощности каждого параметра в трех моделях: DoC, MRDoC и MRDoC2. Мы обнаружили, что модели различались по тому, как на них влияют вопросы 1 и 2, а также по роли, которую играли инструментальные переменные при сравнении MRDoC с MRDoC2. Оценки причинного пути (g1) были смещены в моделях DoC и MRDoC при наличии ошибки измерения фенотипов или при мисспецификации конфаундинга уникальной средой (re) как равного нулю. Мы также обнаружили, что профили мощности различались между моделями. Для MRDoC2 b1, g1 и rf оказывали большое влияние на мощность для отвержения гипотезы, что g1 = 0, в то время как в DoC и MRDoC единственным таким параметром был g1 (Рис. 4). Мы раскрасили Рис. 1, чтобы проиллюстрировать эти результаты: пути, отмеченные синим цветом, имеют смещенные оценки в случае мисспецификации re, те, что отмечены красным, вносят существенный вклад в дисперсию NCP (мощность), а те, что отмечены оранжевым, важны как для мощности, так и смещены из-за мисспецификации re.

При оценке профиля мощности MRDoC (оценивая b2 и фиксируя re=0) мы обнаружили, что сила инструмента не объясняет никакой дисперсии в NCP для отвержения ложной гипотезы об отсутствии причинности. Другими словами, в случае MRDoC нет требования сильного инструмента. MRDoC явно включает горизонтальный плеотропизм в параметр b2. Таким образом, это модель, которая напрямую решает эту проблему, позволяя выявлять причинно-следственные связи с учетом наличия горизонтального плеотропизма. Для идентификации параметра b2 необходимо ограничить другие параметры, такие как rc или re. Следует отметить, однако, что b2 был незначительно смещен из-за неучтенного ненулевого re (Рис. 3).

Эти характеристики MRDoC (отсутствие влияния инструмента на объяснение дисперсии NCP и смещенный b2 при наличии re) вызывают вопрос о том, что MRDoC предоставляет сверх классической оценки причинности DoC. Рис. 2, 3 и 4 показывают, что MRDoC ведет себя очень похоже на DoC с точки зрения смещений и мощности. MRDoC подходил бы в случаях, когда для re существует ранее установленная точная оценка и ее можно зафиксировать, позволяя оценить путь горизонтального плеотропизма (b2). Однако такие оценки вряд ли будут доступны и точны, поэтому требуется альтернатива. Одним из практических подходов было бы использование анализа чувствительности, фиксируя re в диапазоне значений и сообщая полученный b2 для этого диапазона.

В итоге, существует два способа осмысления влияния предположения об отсутствии re на смещение, присутствующее в моделях DoC и MRDoC. Один способ — рассматривать каждый компонент дисперсии как латентный инструмент. Дисперсия E включает ошибку измерения во всех трех протестированных моделях, однако в DoC и MRDoC отсутствие re приводит к тому, что дисперсии E становятся латентными инструментами (PRS являются наблюдаемыми инструментами). Поскольку ошибка измерения поглощается в дисперсии E моделей DoC и MRDoC, это приводит к смещению причинных оценок. Второй способ осмысления этих смещений заключается в том, что отсутствие re вводит эндогенность между экспозицией и исходом, коррелированные ошибки между Trait 1 и Trait 2. В этой ситуации причинные оценки будут смещены аналогично тому, что происходит в линейных регрессиях при наличии коррелированных ошибок в процессе генерации данных (Bollen 2012; Maydeu-Olivares et al. 2019), и b1 не будет действовать как инструментальная переменная (как показано на Рис. 4 в MRDoC). В MRDoC2, поскольку re специфицировано, эти эффекты не возникают.

Оценки параметров из модели MRDoC2 последовательно демонстрировали наименьшее смещение во всех проведенных тестах. Предположение re = 0 и отсутствие частично плеотропных путей, таких как rf*b1 или rf*b3, в MRDoC и DoC искажали оценку причинного пути (g1). Еще одним преимуществом MRDoC2 является ее обратная связь, позволяющая делать выводы о двунаправленной причинности. Петли обратной связи часто встречаются в природе, и большинство современных методов МР (часто основанных на линейной регрессии) могут оценивать этот тип отношений, только запуская тест дважды, за исключением Darrous et al. (2021), меняя инструмент в каждом направлении (Timpson et al. 2011; Hwang and Evans 2024).

Проведенные тесты также выявили важный аспект сравнения моделей в структурном моделировании уравнений (SEM - Structural Equation Modeling). Из-за несамостоятельности параметров модели изменение одного из них обычно приводит к изменениям других параметров (Рис. 2 и 3). Для обеспечения соответствия недавним публикациям (Verhulst et al. 2019; Maes et al. 2022) мы преобразовали все три модели в стиль компонентов дисперсии. Стиль компонентов дисперсии (в отличие от более традиционной спецификации модели ретикулярных действий, RAM - Reticular Action Model) имеет гораздо более откалиброванный уровень ошибки I рода, особенно в многомерном случае (Verhulst et al. 2019).

Данное исследование следует интерпретировать с учетом следующих ограничений. Анализ смещений и результаты анализа мощности этих SEM-моделей служат только для понимания того, как могут возникать смещения и какая мощность в конкретных рассмотренных сценариях. Изменение одного параметра в этих моделях приводит к изменениям большинства других путей, что делает сравнение и интерпретацию непрямыми. Например, установка g2 = 0 в тесте мощности показала, что b3, rf и g2 влияли на дисперсию NCP (не показано).

Представленные модели примечательны тем, что они преодолевают серьезные ограничения, присущие классической МР. MRDoC (с параметром b2, свободно оцененным, и re, зафиксированным на нуле) не требует сильного инструмента, а двунаправленная причинная инференция возможна с использованием кросс-секционных данных. MRDoC включает прямой горизонтальный плеотропизм, как и MRDoC2, которая включает косвенный горизонтальный плеотропизм. Кроме того, модели могут быть расширены на родственников любого типа (например, братьев и сестер), и при наличии таких данных эти модели предлагают интересные новые возможности, такие как истинная двунаправленная причинная инференция или возможность тестирования причинности при контроле горизонтального плеотропизма.