Интересное сегодня
Влияние релевантности эмоциональных лиц на поведенческие реа...
Введение Мотивационная теория эмоций предполагает, что эмоции обладают привилегированным путем обраб...
Как диета влияет на риск развития болезни Альцгеймера: научн...
Болезнь Альцгеймера и питание: как диета влияет на риск Болезнь Альцгеймера — прогрессирующее нейрод...
Метод распознавания именованных сущностей в психомедицине на...
Основные аспекты метода распознавания именованных сущностей (NER) Распознавание именованных сущносте...
Влияние аутизма на жизнь детей до и после диагноза
Введение Аутизм — это нейроразвивающее состояние, которое часто проявляется в раннем детстве и приво...
4 научно обоснованных способа сохранить здоровье мозга
Мозг: самый сложный орган человека Мозг — это самый сложный орган в человеческом организме. Его сеть...
Использование виртуальной реальности для оценки агрессии у п...
Введение Эффективное лечение подростков в условиях судебной системы требует глубокого понимания их л...
Введение
Перистальтическое движение биологических жидкостей является естественным способом перемещения этих жидкостей в некоторых органах живых организмов. Знание перистальтического движения, возникающего в сосудах и каналах в результате сил, представленных градиентами давления, значительно способствует пониманию переноса этих жидкостей внутри организма.
Математическая формулировка
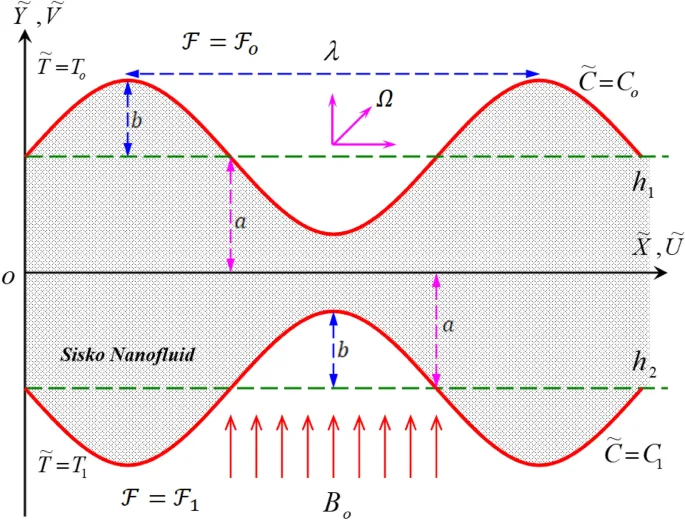
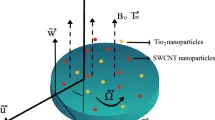
Рассматривается несжимаемое течение не-ньютоновской наножидкости Сиско в симметричном горизонтальном упругом канале. Жидкость движется внутри канала перистальтическим движением через пористую среду под влиянием магнитного поля.
Уравнения сохранения
Уравнение непрерывности для сохранения массы записывается как:
∇ · q = 0
Граничные условия
Соответствующие граничные условия могут быть записаны следующим образом:
- При y = -1 - ε sin 2πx: u = 0, ∂θ/∂y = Bi₂θ
- При y = 1 + ε sin 2πx: u = 0, ∂θ/∂y = Bi₁(1 - θ)
Численные решения
Численный метод Рунге-Кутты является одним из наиболее важных методов численного анализа, используемых для решения систем обыкновенных дифференциальных уравнений. Для решения была использована программа MATLAB с применением функции bvp4c.
Результаты и обсуждение
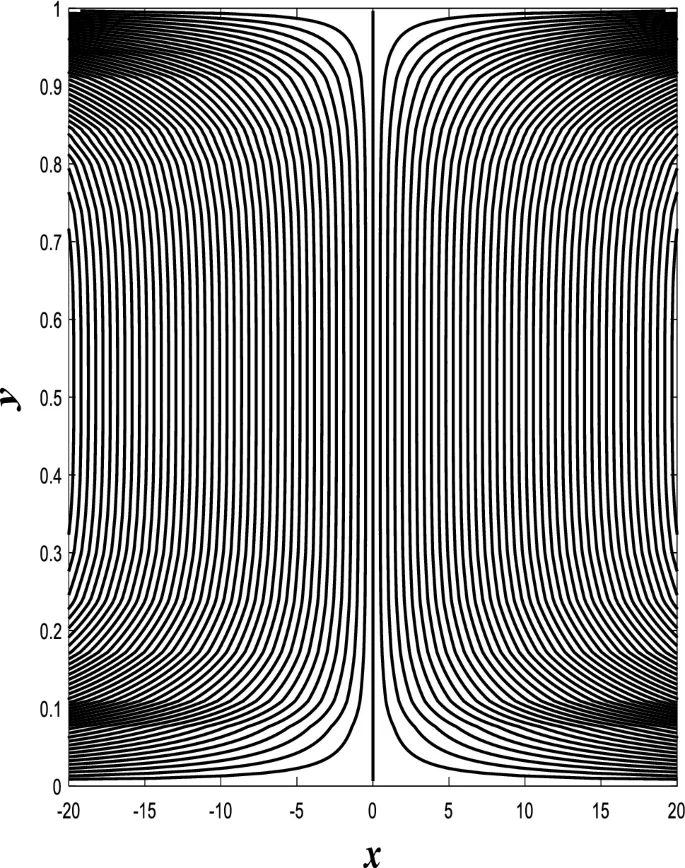
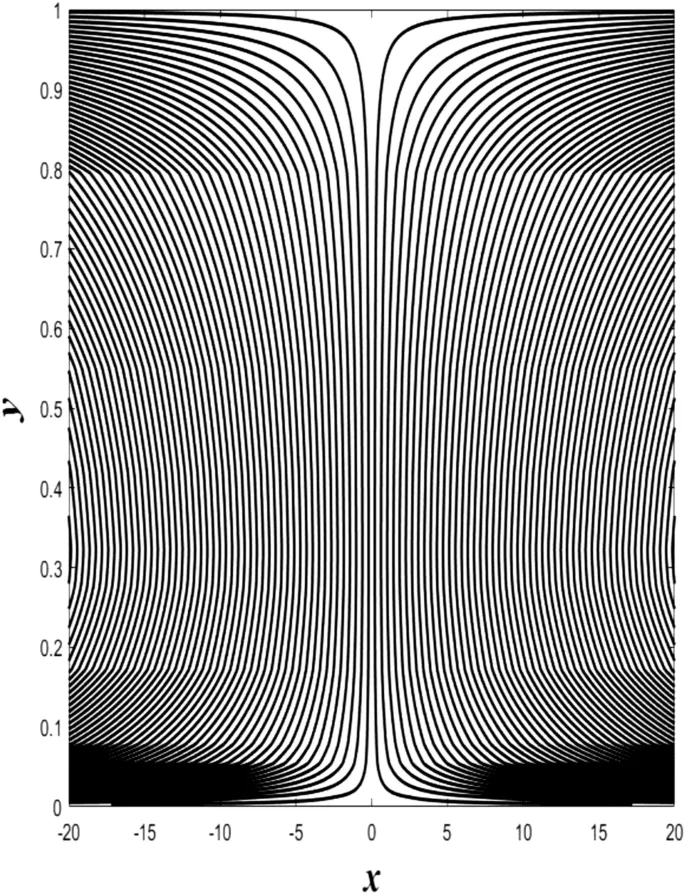
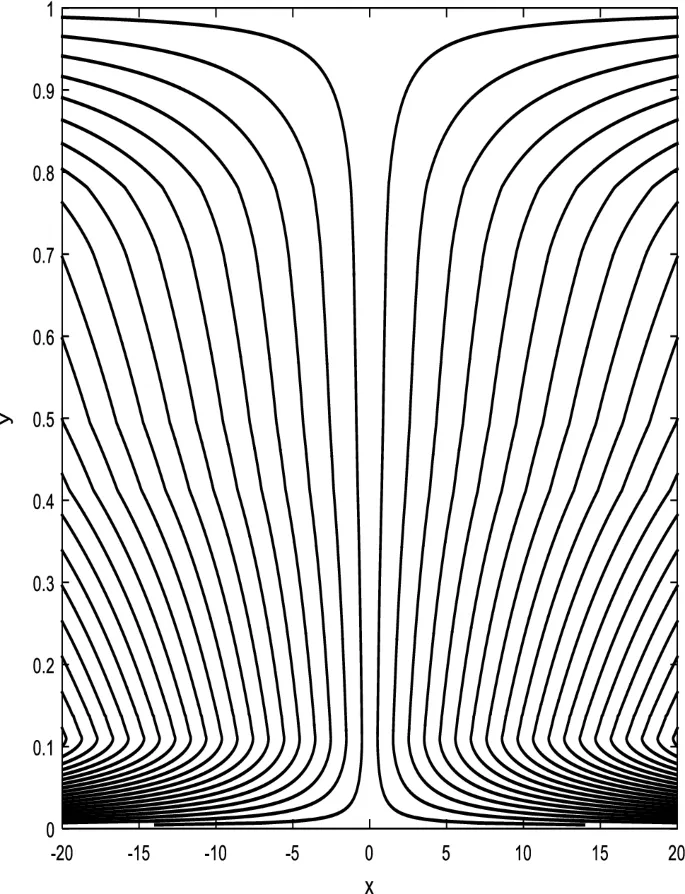
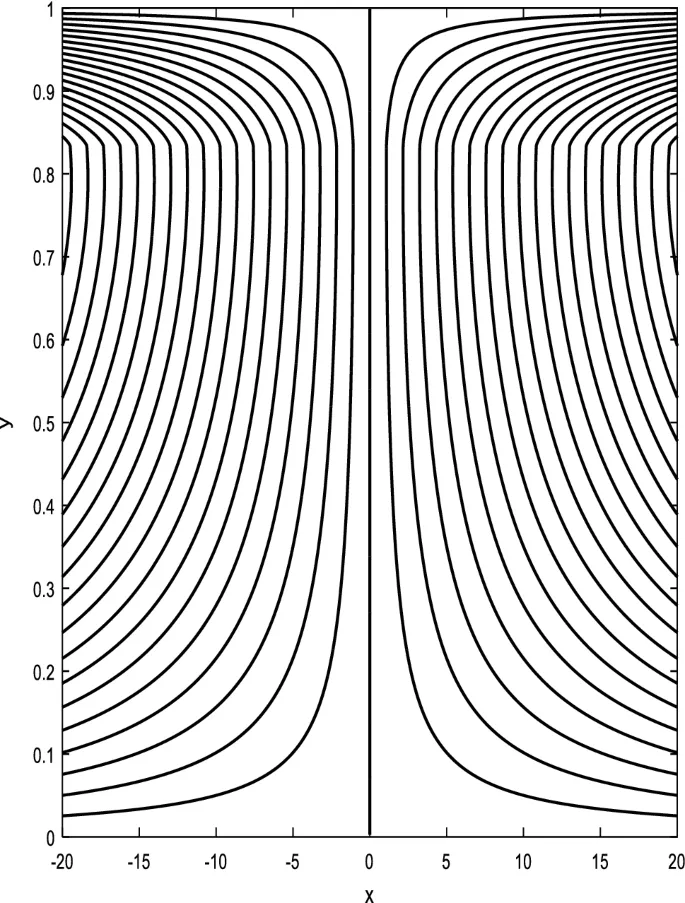
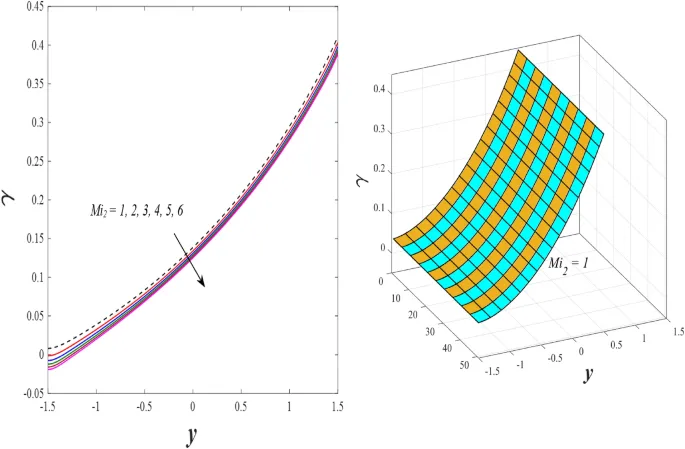
В данном разделе обсуждаются эффекты всех физических параметров на распределения осевой скорости, температуры, солевой концентрации и объемной доли наночастиц.
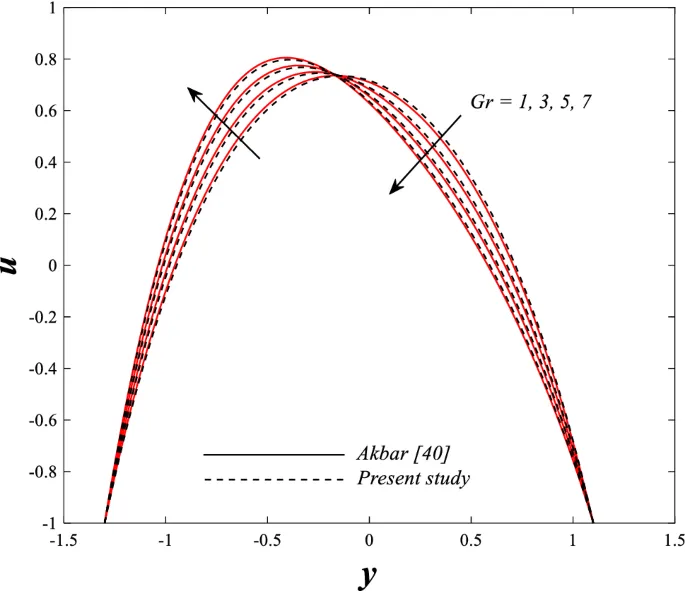
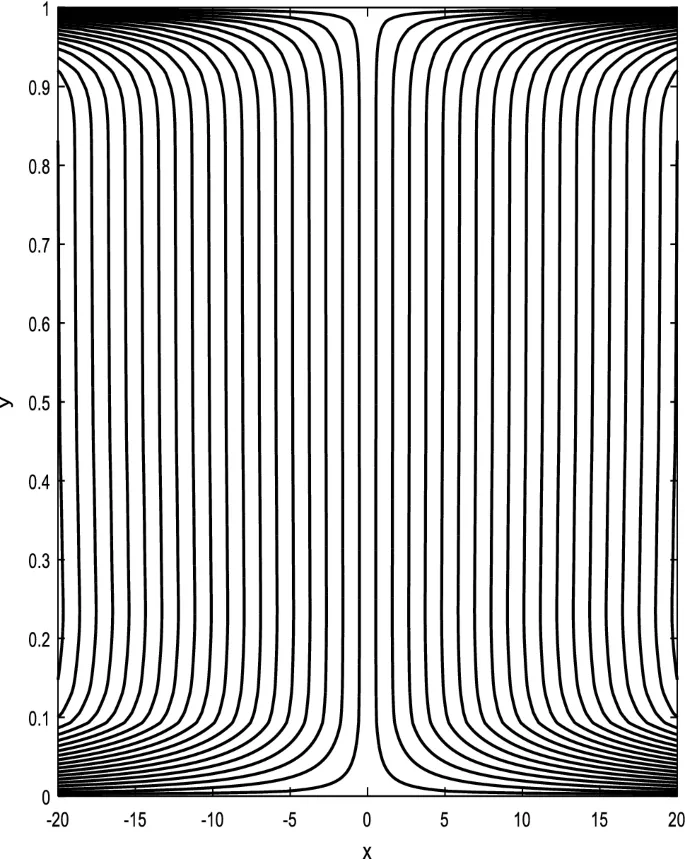
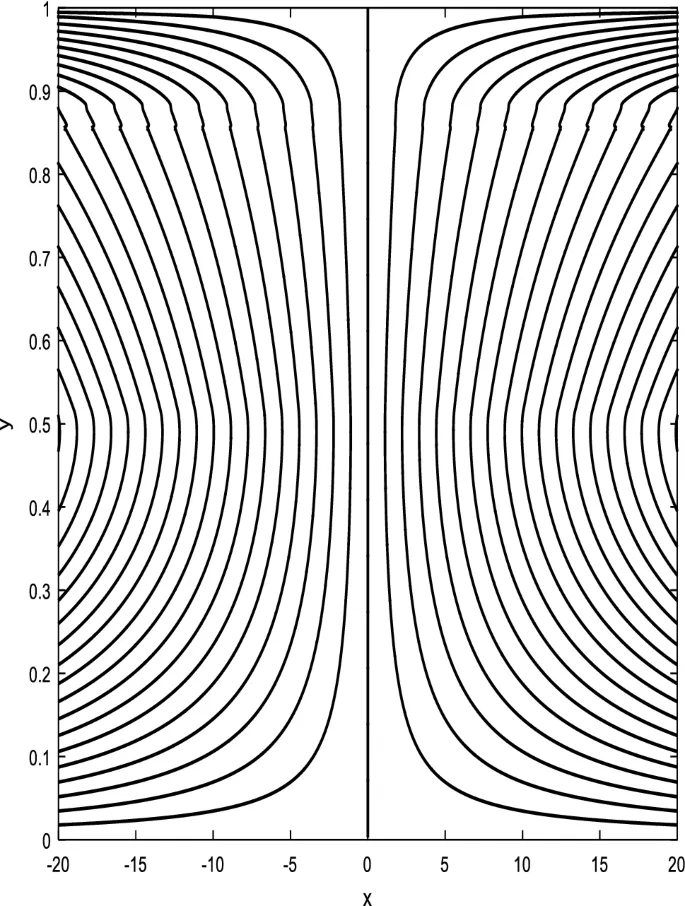
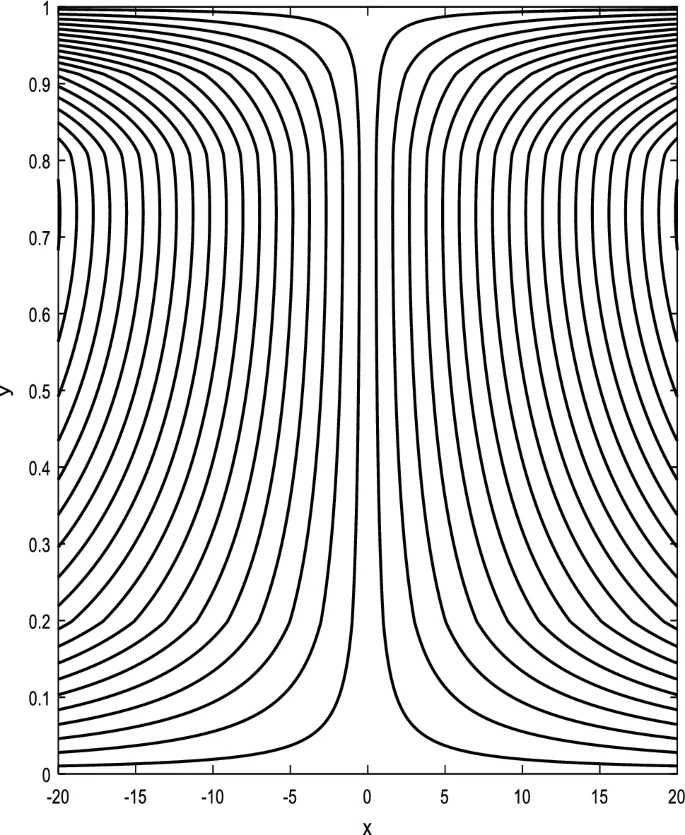
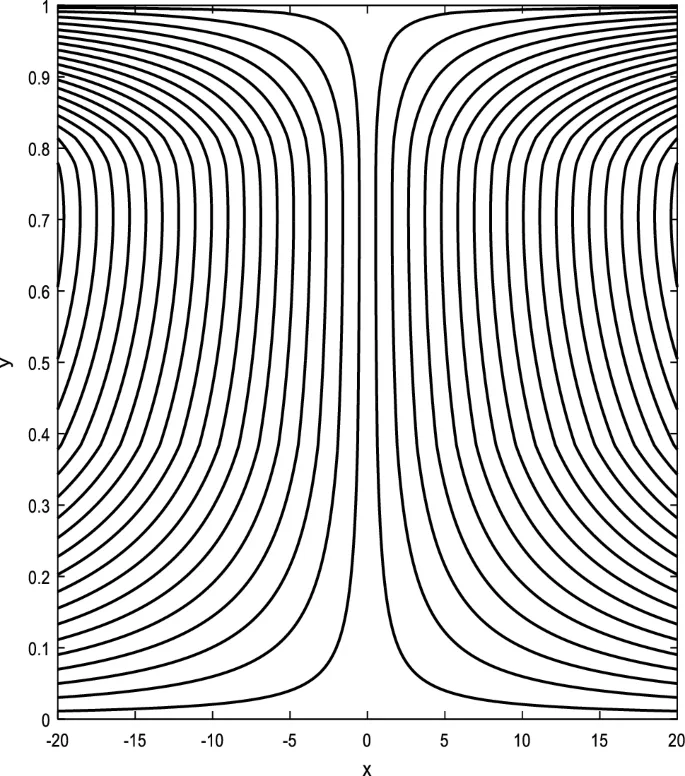
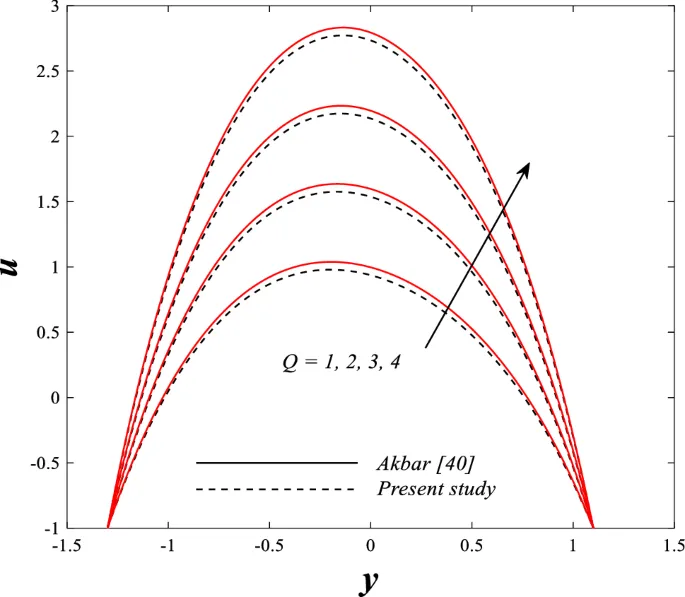
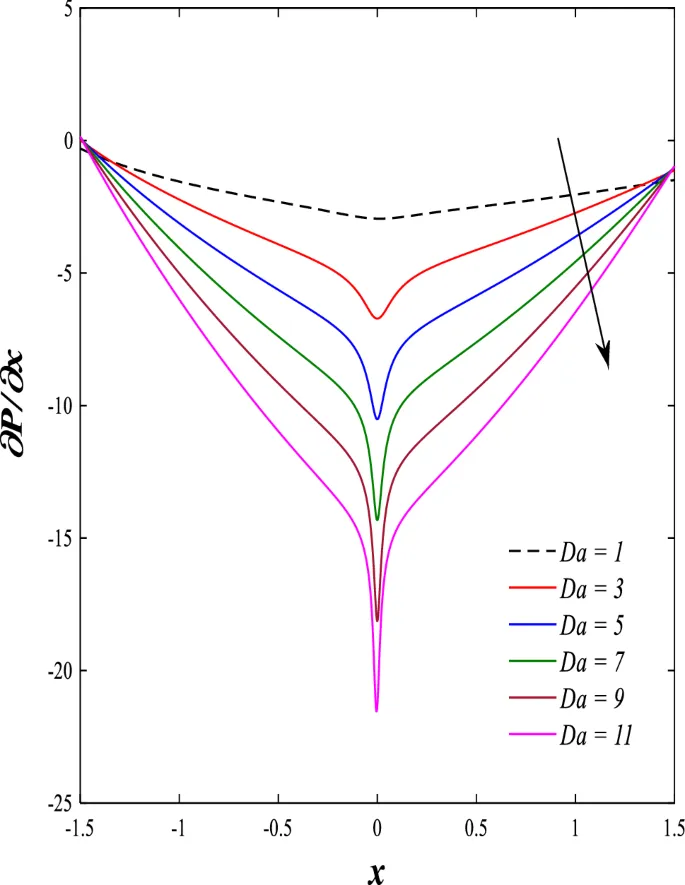
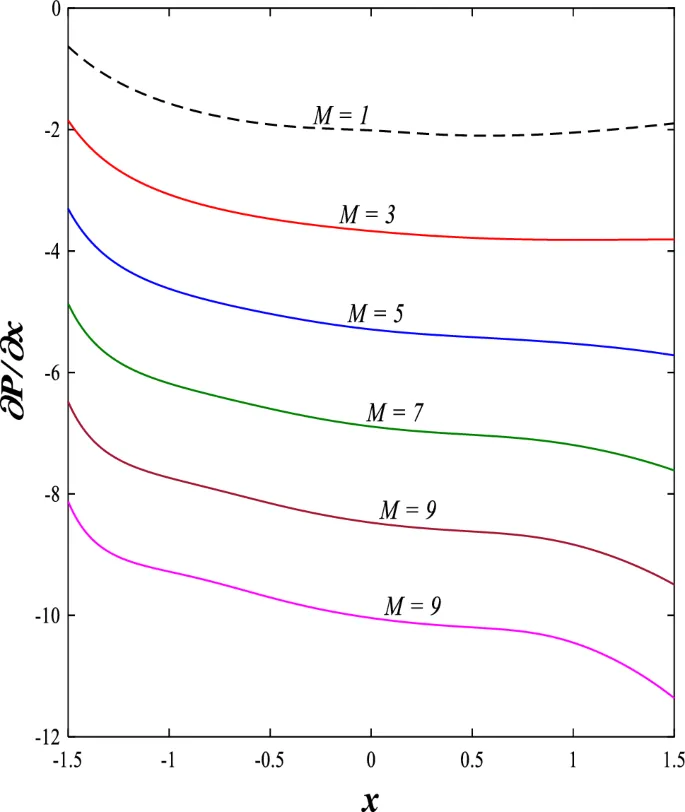
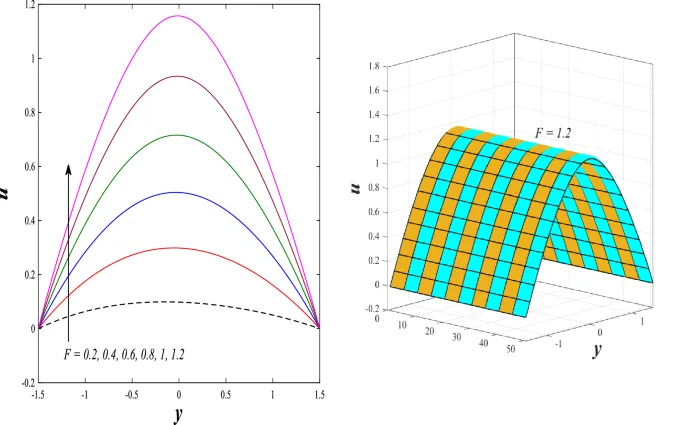
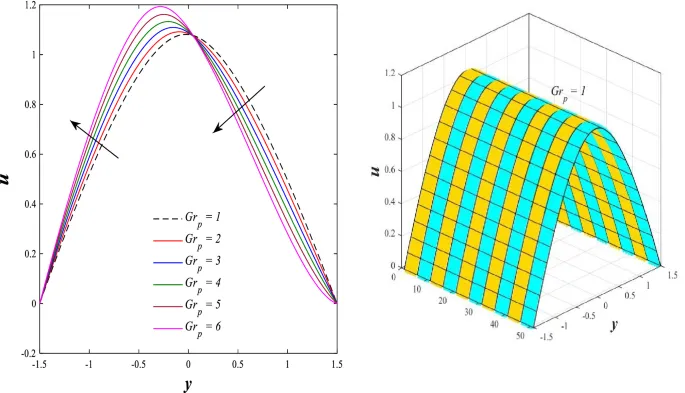
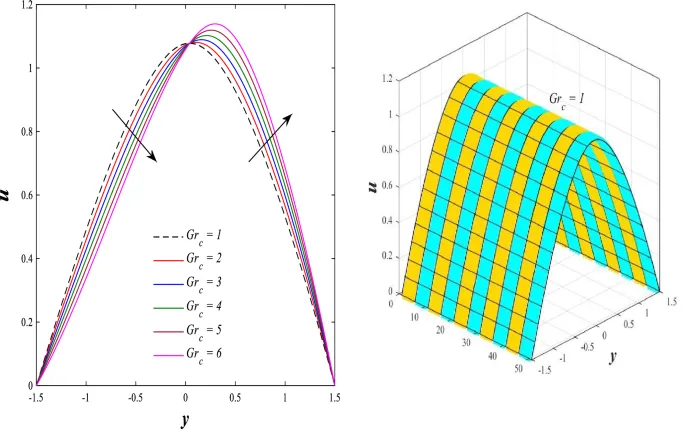
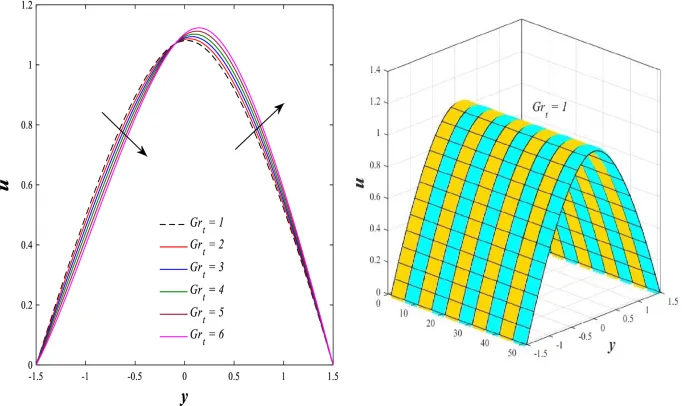
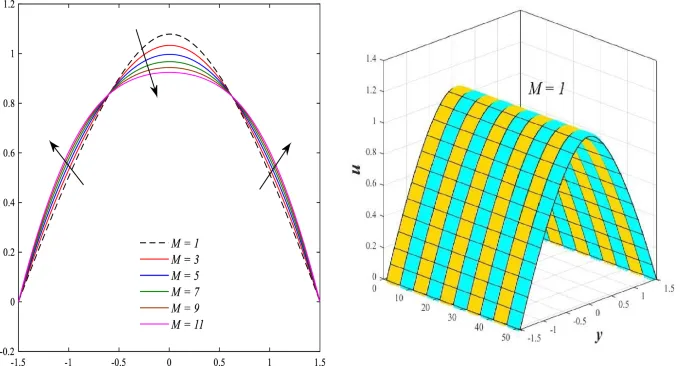
Распределение осевой скорости
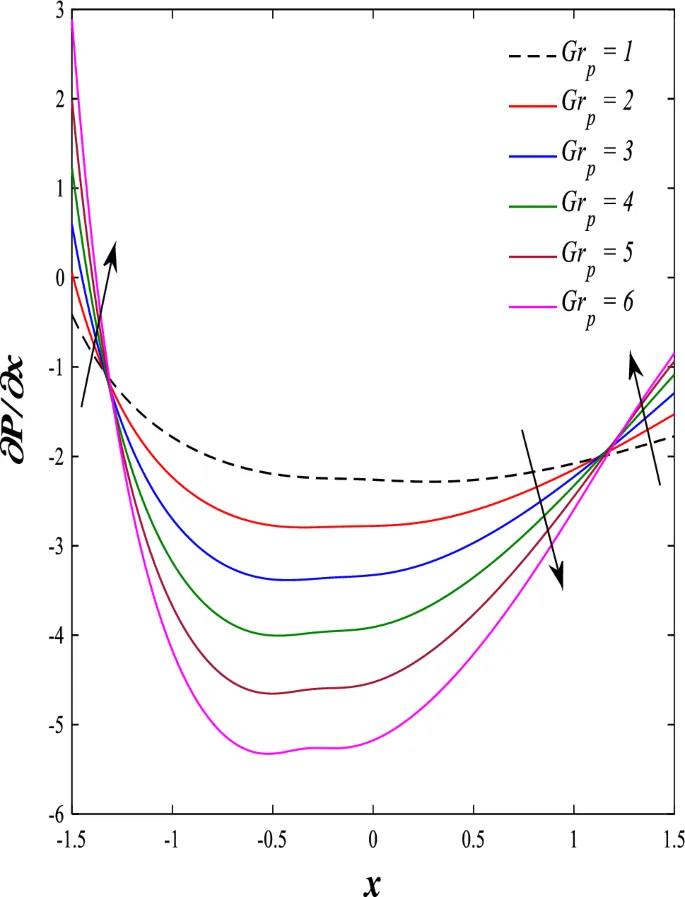
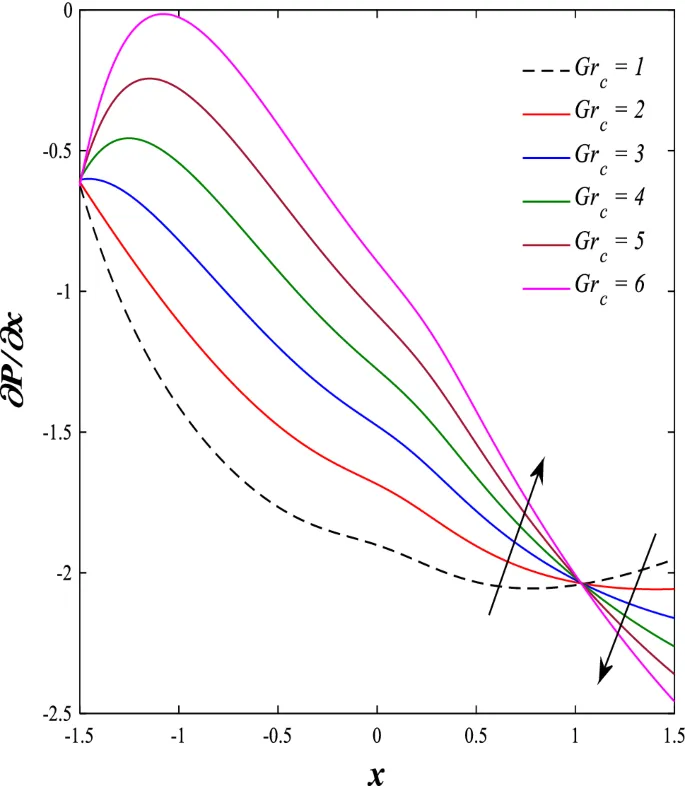
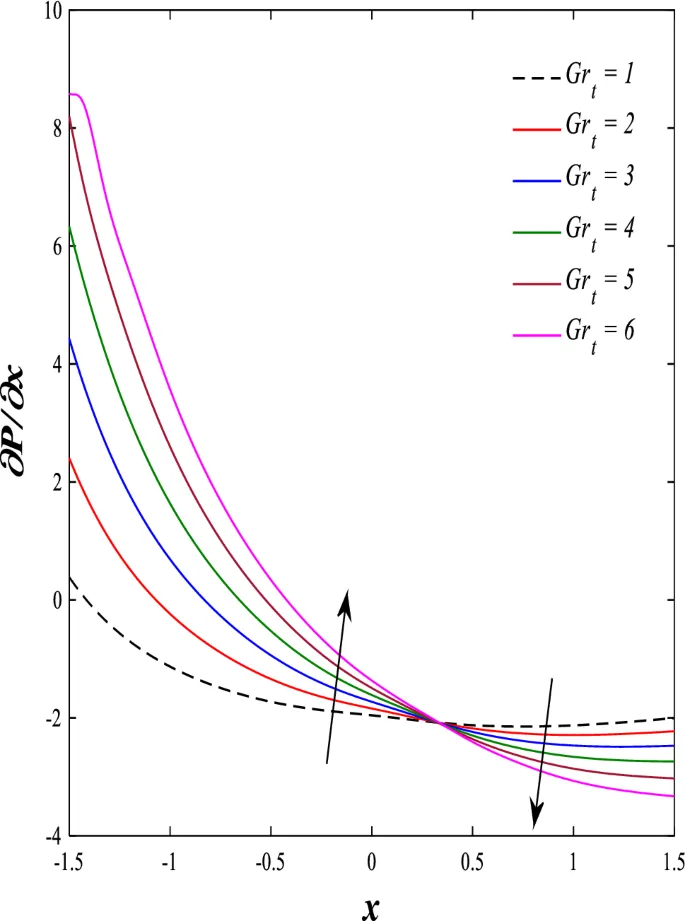
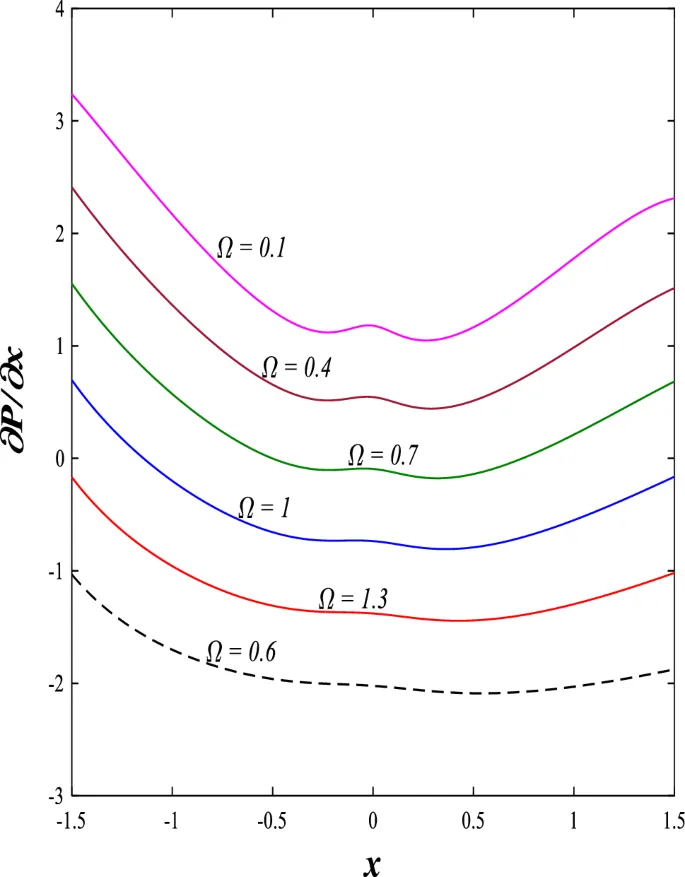
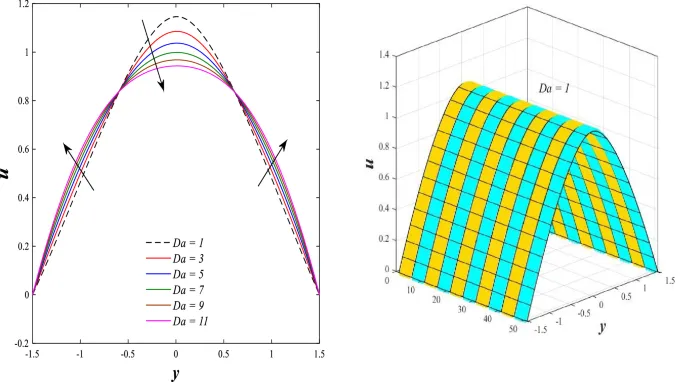
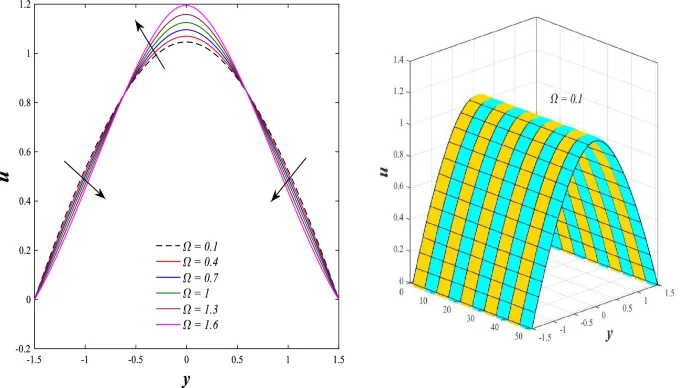
Распределение осевой скорости демонстрирует переменное поведение, изменяясь между увеличением и уменьшением под влиянием магнитного поля, числа Дарси и параметров вращения.
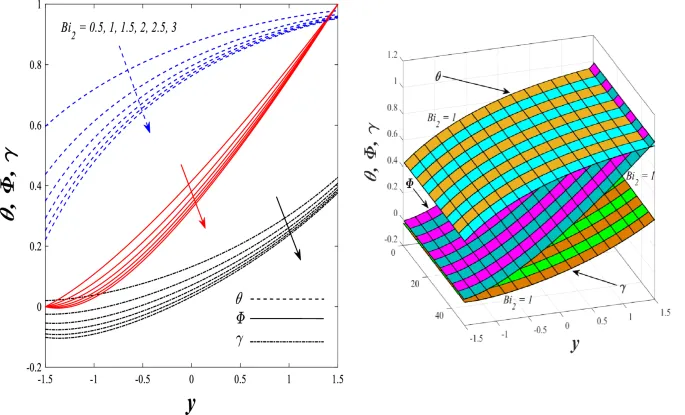
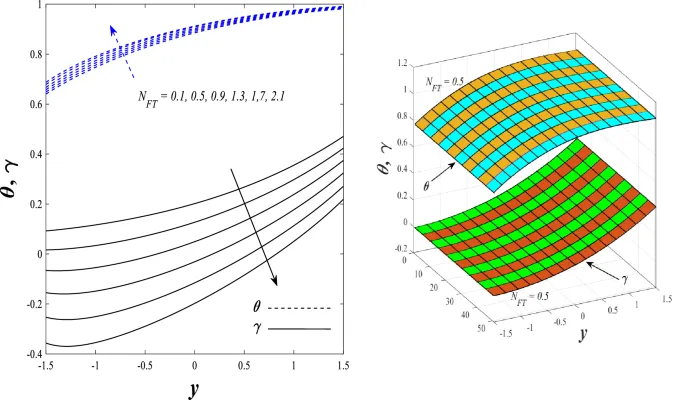
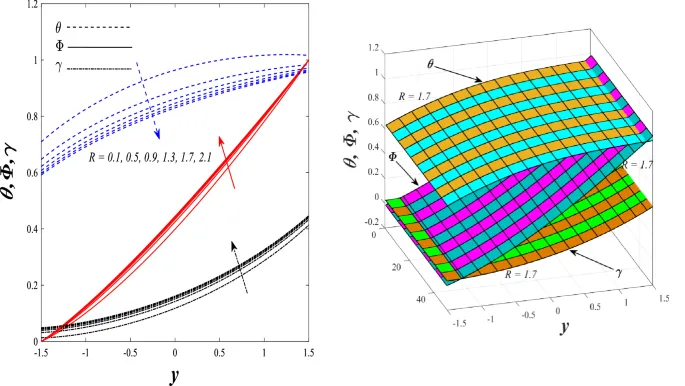
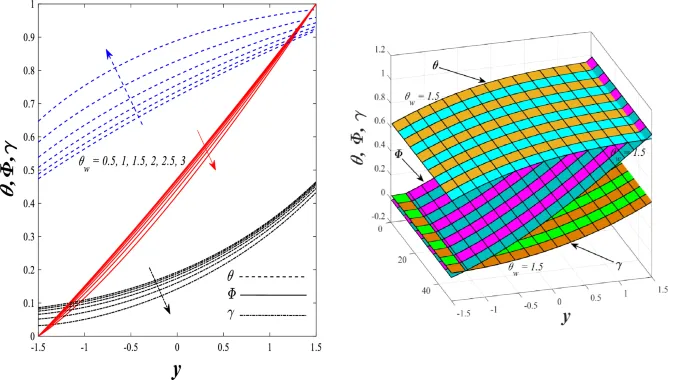
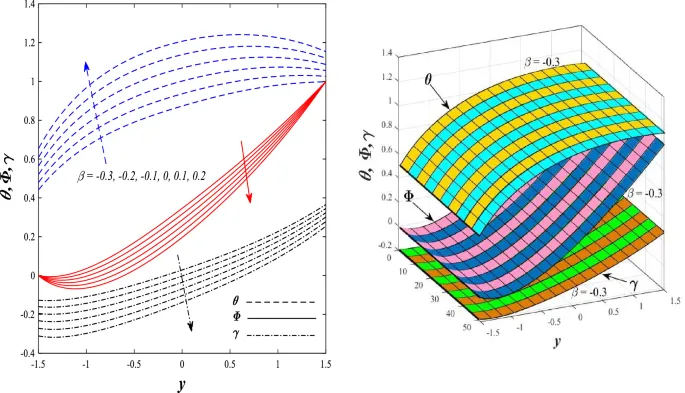
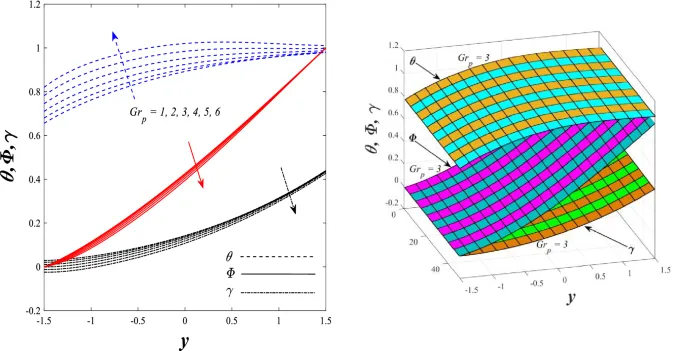
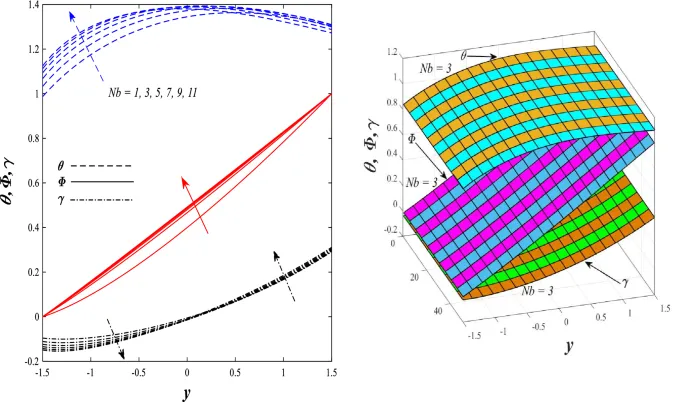
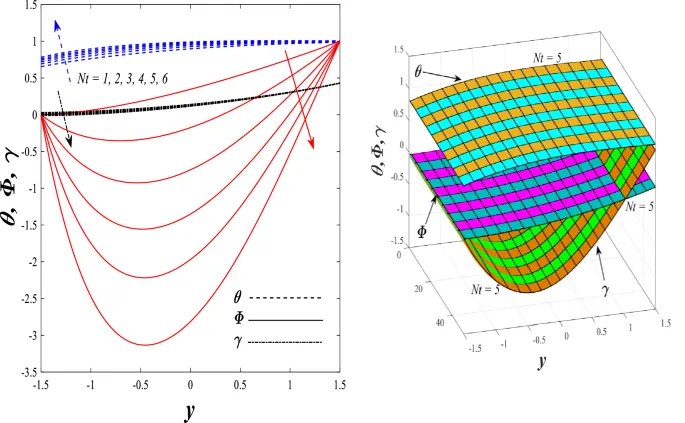
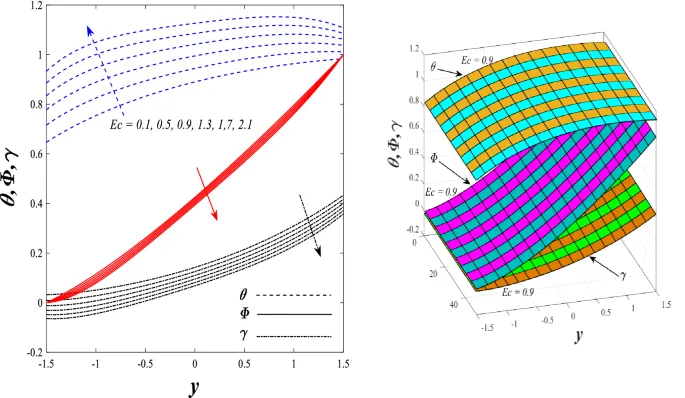
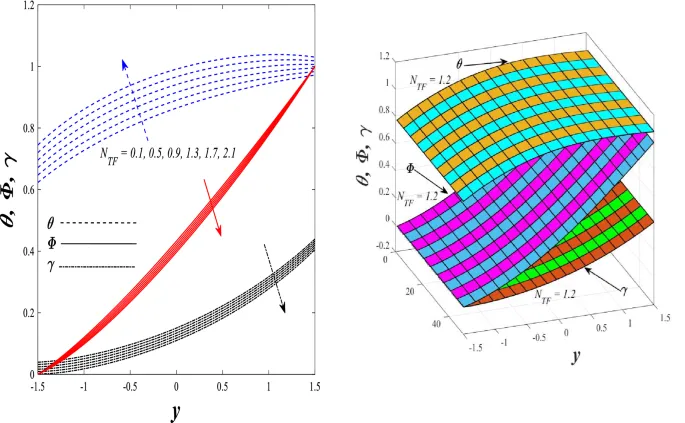
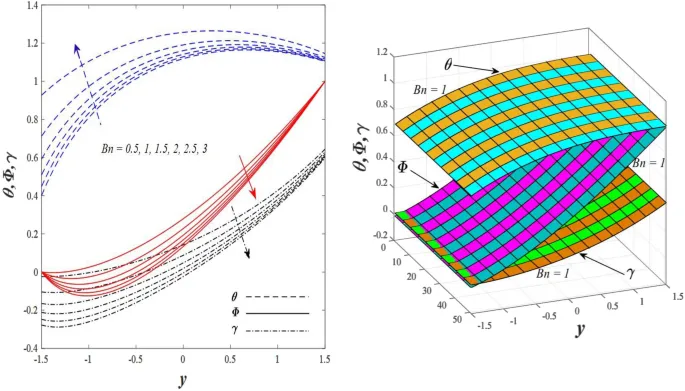
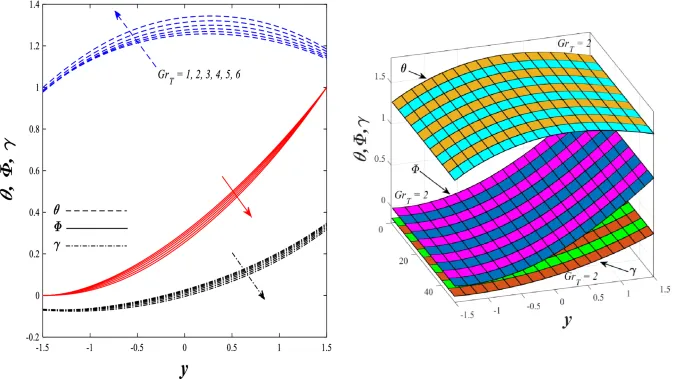
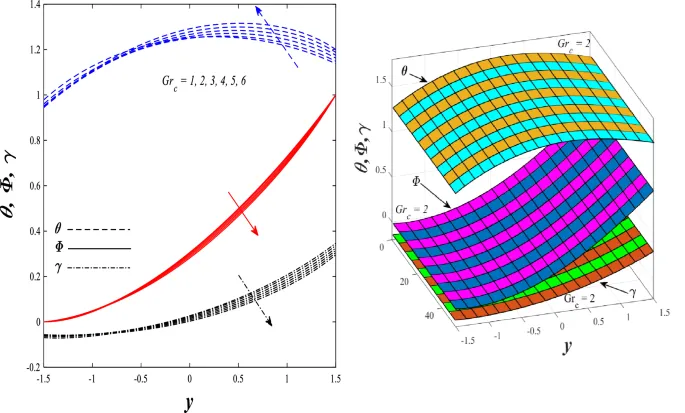
Температурное распределение
Температурное распределение увеличивается под влиянием параметра генерации/поглощения тепла и числа Бринкмана, но уменьшается при увеличении параметра нелинейного теплового излучения.
Заключение
Исследование демонстрирует сложное взаимодействие различных физических параметров на перистальтическое течение наножидкости Сиско. Результаты показывают значительное влияние магнитного поля, пористой среды и тепловых эффектов на характеристики течения.