Коррекция сетевых моделей Изинга при отборе по сумме баллов

В психологических исследованиях все большую популярность приобретают сетевые модели (Borsboom et al., 2021; Robinaugh et al., 2020; Contreras et al., 2019). В этих моделях узлы представляют переменные (например, симптомы психического расстройства или пункты опросника), а ребра — условные ассоциации между переменными (Epskamp & Fried, 2018). Для бинарных переменных наиболее распространенной является модель Изинга (Ising, 1925). Эта модель применяется ко многим психологическим конструктам, включая депрессию (Cramer et al., 2016), установки (Dalege et al., 2016), злоупотребление психоактивными веществами (Rhemtulla et al., 2016) и интеллект (Savi et al., 2019).

Смещения при отборе данных по сумме баллов

Во многих исследованиях сетевого анализа модель Изинга оценивается на основе подвыборки данных, определенной по минимальной сумме баллов моделируемых переменных (например, Hakulinen et al., 2020; Heeren & McNally, 2018; Van Borkulo et al., 2015; Van Rooijen et al., 2018). Это изменяет результирующую сетевую модель по сравнению с моделью, построенной на полной выборке. Например, если все ребра в полных данных представляют положительные линейные ассоциации, то отбор случаев с суммой баллов выше определенного порога приводит к ослаблению положительных ассоциаций, а отсутствующие или слабые ассоциации могут стать отрицательными (De Ron et al., 2021; Epskamp et al., 2022). Если исследователя интересуют только условные ассоциации выбранной таким образом подвыборки, это не является проблемой. Условные ассоциации действительны для конкретной выборки. Однако ребра становятся смещенными, если область выводов исследователя не совпадает с популяцией, отобранной по сумме баллов, например, популяцией, определенной латентным признаком (Haslbeck et al., 2021b).

Более того, изменение ребер становится проблематичным, если исследователь хочет содержательно интерпретировать ассоциации, например, для формирования гипотез о причинно-следственных связях между переменными. Даже если мы анализируем интересующее нас распределение вероятностей, гипотезы о причинных эффектах становятся недействительными после кондиционирования на сумму баллов (Griffith et al., 2020; Haslbeck et al., 2021b). Это связано с тем, что ослабление ребер после отбора по сумме баллов отражает не причинно-следственную связь между переменными, а является результатом кондиционирования на общий эффект (коллидер) переменных, а именно их сумму баллов.

Между тем, формирование гипотез о причинных эффектах, пожалуй, является центральной мотивацией исследователей для оценки сетевых моделей (Borsboom & Cramer, 2013; Epskamp et al., 2018a).

Предлагаемое решение

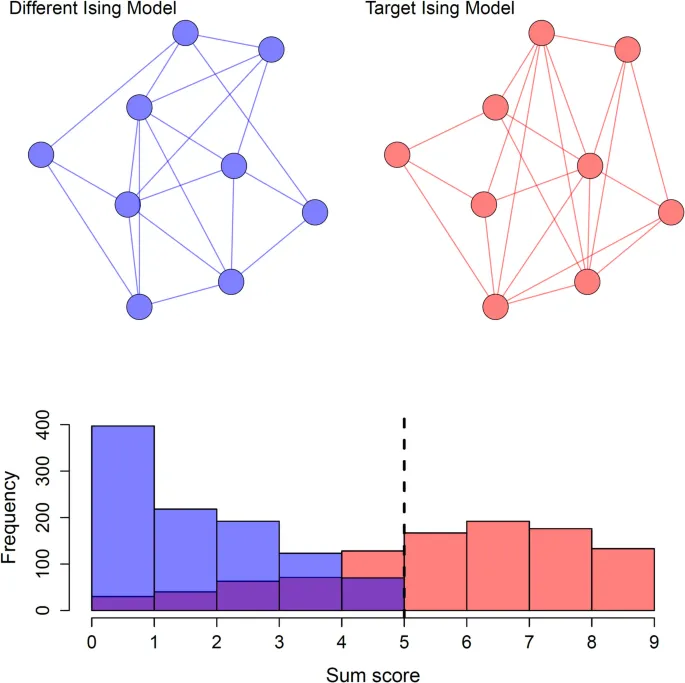
Решением проблемы смещения после отбора по сумме баллов было бы просто не использовать кондиционирование по сумме баллов (Dablander et al., 2019; Haslbeck et al., 2021b). Однако существуют два сценария, проиллюстрированных на Рис. 1, когда это неудовлетворительно, и мы предпочли бы отобрать данные по сумме баллов и скорректировать оценки впоследствии, чтобы получить улучшенные оценки модели Изинга в интересующей популяции.

Сценарий 1: Ограниченная доступность данных

Данные доступны только для части популяции, которая отбирается по сумме баллов (Рис. 1, красная целевая популяция, достигающая выбранного порога суммы баллов), но интересующая популяция — это целевая популяция независимо от суммы баллов (Рис. 1, полная красная целевая популяция, включая случаи в фиолетовой части распределения).

Сценарий 2: Наличие субпопуляций

Выборка состоит из двух или более субпопуляций: целевой популяции (Рис. 1, красная целевая популяция) и как минимум одной другой популяции (Рис. 1, синяя другая популяция), которая частично пересекается с целевой популяцией (фиолетовая часть рисунка представляет собой пересечение популяций). Критерий отсечения по сумме баллов выбирает часть целевой популяции, но не всех. Более того, никто из другой популяции не достигает выбранного критерия отсечения. На Рис. 1 видно, что фиолетовая часть распределения не достигает суммы баллов, которая находится на черной пунктирной линии, но частично состоит из людей из обеих популяций.

Сценарий 1 может возникнуть, например, если исследование включает диагноз психического расстройства в качестве критерия включения, который основан на сумме баллов симптомов, поскольку определение психических расстройств в значительной степени зависит от наличия симптомов (Borsboom et al., 2016). Сценарий 2 может возникнуть, когда предполагается наличие двух или более субпопуляций, описываемых различными моделями Изинга и не охватываемых какой-либо измеренной переменной, которую можно было бы использовать для их различения (т.е. они латентны). Хотя мы не можем проверить, так ли это на самом деле, это может быть правдоподобно в ситуациях, когда две предполагаемые популяции тесно связаны с суммой баллов. Опять же, пример — случай психического расстройства, когда можно предположить наличие латентного признака, например, уязвимости, который тесно связан, но не эквивалентен сумме баллов симптомов.

В описанных выше двух сценариях оценка модели Изинга на подвыборке данных приводит к смещенным оценкам для целевой популяции. В данной статье мы предлагаем коррекцию для оценки модели Изинга для целевой популяции на основе данных, отобранных по критерию отсечения суммы баллов. Эта коррекция приводит к несмещенным оценкам модели Изинга для целевой популяции в описанных выше сценариях. Мы реализовали нашу коррекцию в четырех часто используемых пакетах для оценки модели Изинга: IsingFit (Van Borkulo & Epskamp, 2023), IsingSampler (Epskamp, 2023a), bootnet (Epskamp et al., 2018a, 2018b) и psychonetrics (Epskamp, 2023a, 2023b).

Сначала мы опишем, как предложенный нами метод оценки корректирует смещение выборки при отборе по сумме баллов. Во-вторых, мы продемонстрируем, что наша коррекция работает в симуляционном исследовании с использованием эмпирических сетевых параметров. Поскольку сеть полной популяции известна в этой ситуации, мы можем оценить, насколько хорошо наша коррекция восстанавливает сеть, генерирующую данные, по сравнению с обычной оценкой. Наконец, мы приведем пример с использованием симулированных данных и данных National Comorbidity Study Replication (NCRR; Kessler & Merikangas, 2004), чтобы помочь исследователям в выводах, которые они могут сделать после использования нашей коррекции с эмпирическими данными.

Коррекция смещения выборки

Наиболее популярной сетевой моделью для бинарных данных является модель Изинга (Ising, 1925; Epskamp, 2017), которая моделирует распределение вероятностей многомерных бинарных данных с набором порогов для каждой переменной и парными ассоциациями между каждой парой переменных. Модель Изинга может быть оценена с использованием многомерной и одномерной оценки. Многомерная оценка оптимизирует параметры модели с учетом имеющихся данных, используя совместное распределение вероятностей для одновременной оценки всех параметров (например, Epskamp et al., 2022). Одномерная оценка максимизирует псевдоправдоподобие данных путем подгонки нескольких логистических регрессий, где коэффициенты напрямую соответствуют условным ассоциациям модели Изинга (Epskamp et al., 2022; Marsman et al., 2018). Хотя многомерная оценка обычно должна быть более точной (например, Brusco et al., 2022; или для модели экспоненциальной случайной графовой модели см. Van Duijn et al., 2009), она вычислительно сложна. Хотя модель Изинга остается вычислительно управляемой для большинства размеров сетей, встречающихся в психологических сетевых исследованиях, реализации на R, обычно используемые для этих сетей, часто не могут оценить сети с более чем 20 узлами (Finnemann et al., 2021; Epskamp, 2017; Van Borkulo et al., 2014).

Многомерная оценка и коррекция

Модель Изинга может быть выражена как совместное распределение вероятностей следующим образом:

$$Preft({{arvec{Y}}}_{{arvec{p}}}={{arvec{y}}}_{{arvec{p}}} ight)=rac{1}{Z}expeft(umimits_{i}{{ au }_{i}y}_{pi }+umimits_{}{{mega }_{ij}y}_{pi}{y}_{pj} ight)$$

где {{arvec{Y}}}_{{arvec{p}}} — вектор бинарных ответов человека p на m пунктов или узлов, а {{arvec{y}}}_{{arvec{p}}} — конкретное состояние {{arvec{Y}}}_{{arvec{p}}} (например, вектор из 0 и 1, когда симптом отсутствует или присутствует соответственно). Z — нормализующая константа относительно данных (Epskamp et al., 2022), такая, что сумма вероятностей всех возможных реализаций {{arvec{Y}}}_{{arvec{p}}} равна 1:

$$Z = um_{{arvec{y}}}expeft(umimits_{i}{{ au }_{i}y}_{pi}+umimits_{}{{mega }_{ij}y}_{pi}{y}_{pj} ight)$$

Часть уравнения, которая суммируется здесь, называется потенциалом, Pot({{arvec{Y}}}_{{arvec{p}}}={{arvec{y}}}_{{arvec{p}}}), что можно понимать как ненормализованную вероятность того, что {{arvec{Y}}}_{{arvec{p}}} демонстрирует шаблон ответа {{arvec{y}}}_{{arvec{p}}}. В функции потенциала модели Изинга { au }_{i} представляет собой порог узла i, который можно понимать как предпочтение узла определенного значения. Кроме того, {mega }_{ij} представляет собой парное взаимодействие между узлами i и j. Если этот параметр положителен, состояния, в которых узлы i и j имеют одинаковое значение, становятся более вероятными. И наоборот, если {mega }_{ij} отрицателен, состояния, в которых узлы i и j имеют разные значения, становятся более вероятными.

Критически важно для нашей коррекции: при оценке модели Изинга после отбора по сумме баллов смещение возникает из-за того, что Z по-прежнему суммируется по всем возможным реализациям {{arvec{y}}}_{{arvec{p}}}. Однако мы достоверно знаем, что шаблоны ответов, сумма баллов которых ({s}_{p}) не достигает нашего критерия отсечения k, больше невозможны, поскольку для всех случаев в данных выполняется:

$${s}_{p}=umimits_{i}{y}_{pi}e k.$$

Чтобы это исправить, мы должны вместо этого моделировать условное распределение вероятностей:

$$Preft({{arvec{Y}}}_{{arvec{p}}}={{arvec{y}}}_{{arvec{p}}}| {s}_{p}e k ight)$$

Мы можем сделать это, суммируя только по шаблонам ответов, где {s}_{p}e k при вычислении Z:

$${Z}^{eft(k ight)}=umimits_{y, se k}expeft(um olimits_{i}{ au }_{i}{y}_{pi}+umimits_{}{{mega }_{ij}y}_{i}{y}_{j} ight)$$

Если мы используем {Z}^{eft(k ight)} вместо Z в исходной модели Изинга, модель должна быть оценена без смещения, возникающего из-за отбора по сумме баллов. Например, в очень простом случае трех переменных, которые могут быть либо присутствовать (1), либо отсутствовать (0), и критерия отсечения суммы баллов 2, это означало бы, что мы вычисляем Z, суммируя потенциалы всех возможных шаблонов ответов, которые остаются возможными после нашего отбора:

$$Z = Pot({arvec{Y}} = [ ext{1,1},0]) + Pot({arvec{Y}} = [ ext{1,0},1]) + Pot({arvec{Y}} = [ ext{0,1},1] + Pot({arvec{Y}} = [ ext{1,1},1]).$$

Мы просто исключили все остальные потенциалы шаблонов ответов и затем можем продолжить оценку параметров модели Изинга как обычно. Отметим, что наша коррекция делает многомерную оценку гораздо более управляемой, уменьшая пространство, над которым вычисляется нормализующая константа.

Одномерная оценка и коррекция

Интуиция, лежащая в основе нашей коррекции для одномерной оценки, аналогична многомерной. Вместо вычисления псевдоправдоподобия данных, в котором используются узловые регрессии для моделирования каждой переменной как зависимой переменной, а всех остальных переменных — как независимых, мы вычисляем псевдоправдоподобие данных, условное на наш критерий отсечения k. То есть, модель логистической регрессии для первой переменной, {y}_{1}, при условии всех остальных переменных {athbf{y}}_{p}^{eft(1 ight)} и условия, что сумма баллов достигает нашего критерия отсечения k, становится:

$$Pr({Y}_{1} ={y}_{1}| {{arvec{Y}}}_{p}^{eft(1 ight)}={athbf{y}}_{p}^{eft(1 ight)}, {s}_{p}e k) = rac{Pr({Y}_{1} ={y}_{1}, {{arvec{Y}}}_{p}^{eft(1 ight)}={athbf{y}}_{p}^{eft(1 ight)},{s}_{p}e k)}{um_{{y}_{i}}Pr({Y}_{1} = {y}_{i},{{arvec{Y}}}_{p}^{eft(1 ight)}={athbf{y}}_{p}^{eft(1 ight)}, {s}_{p}e k )}$$

в котором um_{{y}_{i}} суммирует оба возможных исхода {y}_{i}. Однако существует одна ситуация, в которой нам не нужно суммировать оба возможных исхода {y}_{i}: когда сумма других переменных равна k-1, поскольку ответ {y}_{1} может быть только 1, чтобы получить достаточную сумму баллов для включения в выборку.

Проиллюстрируем это на примере модели Изинга с пятью симптомами, {y}_{1} по {y}_{5}, где 1 указывает на присутствие симптома, а 0 — на его отсутствие. Мы вычисляем сумму баллов для всех ({s}_{p}), и мы включаем в анализ данных только тех лиц, которые достигают как минимум критерия отсечения k (т.е. {s}_{p} ≥ k). Если мы теперь подгоним логистическую регрессию {y}_{1} с другими симптомами в качестве предикторов, существует одна ситуация, в которой наш критерий отсечения дает информацию об исходе, а именно когда сумма баллов предикторов равна k-1. Это связано с тем, что мы уже достоверно знаем, что:

$$Preft({y}_{1}=1 |{s}_{p}^{(1)}=k-1, {s}_{p}e k ight)=1,$$

где {s}_{p}^{(1)} — сумма баллов без {y}_{1}, {um }_{i=2}^{p}{y}_{i}. Если известно, что сумма других симптомов равна k-1, то предсказанный симптом должен присутствовать. Таким образом, для коррекции смещения выборки мы должны установить правдоподобие данных равным 1 для всех случаев, где это верно. На практике это означает, что в одномерных регрессионных моделях случаи, для которых сумма предикторов равна k-1, могут быть удалены.

Симуляционное исследование

Основная цель нашего симуляционного исследования заключалась в сравнении эффективности нашей коррекции с некорректированной, обычной оценкой при восстановлении «истинной» сетевой структуры после отбора на основе критерия суммы баллов. Мы использовали истинную сетевую структуру для генерации бинарных данных, которую мы считаем правдоподобной в психологических сетевых исследованиях (т.е. плотную сеть с множеством положительных ребер).

Процедура симуляции

Мы использовали статистическое программное обеспечение R для всех анализов (R Core Team, 2016). Код R и материалы доступны по адресу https://github.com/Jesse291847/Correctingforselectionbias. Симуляционное исследование состояло из трех шагов. На шаге 1 мы построили «истинную» сеть, из которой сгенерировали бинарные данные. На шаге 2 мы отобрали случаи из сгенерированных данных, которые достигли выбранного критерия суммы баллов, и оценили сети с коррекцией и без нее, с использованием трех различных пакетов: IsingFit, IsingSampler и psychonetrics. На шаге 3 мы сравнили, насколько оцененная сеть с коррекцией и без нее напоминала истинную сеть.

Мы оценили сети для четырех различных размеров выборки (т.е. 500, 1000, 2500 и 5000) и трех различных критериев отбора по сумме баллов (т.е. 0, 2 и 5). В этом контексте размер выборки относится к размеру выборки после отбора по сумме баллов, если применимо. Мы выбрали критерий отсечения ноль, чтобы иметь базовую точность каждого оценщика для сравнения производительности нашей коррекции. Мы выбрали 2 и 5, чтобы исследовать, насколько пагубен более высокий критерий отсечения суммы баллов для восстановления истинной сети. Мы провели каждую kondisiю 100 раз и оценили шесть сетей в каждом прогоне, т.е. скорректированную и нескорректированную сеть с каждым из трех пакетов. Единственным исключением было при оценке на полной выборке, где мы оценили три сети, поскольку в этом случае нет разницы между скорректированной и нескорректированной сетью. Это привело к общему числу 1200 прогонов (4 размера выборки × 3 критерия отсечения × 100 повторений). Мы подробно опишем каждый шаг симуляции в следующих разделах.

Шаг 1: Генерация данных

Мы использовали параметры веса ребер и пороговые параметры из Cramer et al. (2016) для симуляции данных с использованием функции IsingSampler (Epskamp, 2023a). В принципе, любая сетевая структура может подтвердить, что наша коррекция работает. Однако использование эмпирически информированных параметров гарантирует, что наша истинная сеть имеет структуру, которая может быть правдоподобной в эмпирических исследованиях. Сеть из Cramer et al. (2016) была оценена с использованием данных первого интервью Virginia Adult Twin Study of Psychiatric and Substance Use Disorders (VATSPSUD; Kendler & Prescott, 2006; Prescott et al., 2000). Эти данные содержат информацию о наличии или отсутствии 14 детализированных симптомов депрессии из Diagnostic and Statistical Manual of Mental Disorders, Third Edition, Revised (DSMIIIR; American Psychiatric Association, 1987) для 8937 участников. Интервью проводились обученными специалистами в области психического здоровья, которые оценивали наличие каждого симптома. Когда симптом присутствовал, интервьюер убеждался, что симптом не был вызван физической проблемой.

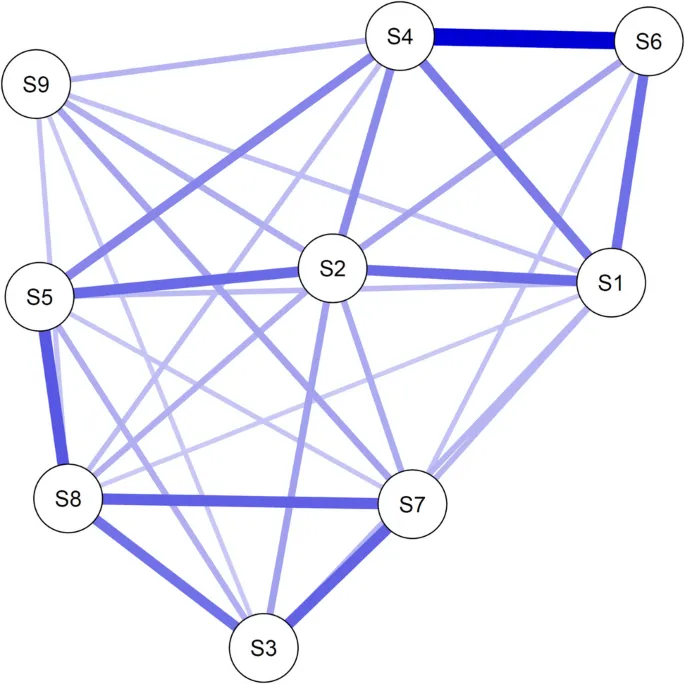
Мы агрегировали некоторые симптомы, чтобы сохранить девять основных симптомов большого депрессивного расстройства (БДР) из DSM5 (American Psychiatric Association, 2013). Подробности получения истинной сети см. в Приложении А. На Рис. 2 показана результирующая истинная сеть. Несмотря на небольшие адаптации оригинальной сети, результирующая структура остается схожей со структурами, ожидаемыми в психологических эмпирических исследованиях. Плотность (т.е. доля присутствующих ребер от всех возможных ребер) составила 0,81; все 29 присутствующих ребер были положительными, а средняя сила ребра — 0,61.

Шаг 2: Оценка сети

Из сгенерированных данных мы отобрали случаи, которые достигли критерия отсечения суммы баллов (т.е. 0, 2 или 5). Мы использовали подвыборку данных для оценки скорректированной и нескорректированной сети с использованием трех различных пакетов: IsingFit (одномерная оценка; Van Borkulo & Epskamp, 2023), IsingSampler (одномерная оценка; Epskamp, 2023a) и psychonetrics (многомерная оценка; Epskamp, 2023a, 2023b). С функцией IsingFit мы использовали узловые логистические регрессии в сочетании с регуляризацией Lasso (Tibshirani, 1996) с расширенным байесовским информационным критерием (EBIC) (Chen & Chen, 2008) для выбора модели (где некоторые параметры принудительно устанавливаются в ноль, и различные модели сравниваются для минимизации статистики EBIC; см. Van Borkulo et al., 2014, для подробностей). С функцией IsingSampler мы использовали узловые регрессии с пороговой обработкой в соответствии с правилом AND (α = 0,01), где в сеть включаются только ребра, значимые в обоих направлениях. С пакетом psychonetrics мы использовали отсечение (pruning), где алгоритм удаляет незначимые ребра (α = 0,01), а затем переоценивает сеть.

Шаг 3: Меры исхода

Мы сравнили оцененные сети с истинной сетью на основе общей ошибки веса ребер, которая является разницей между истинными и оцененными весами ребер. Для вычисления общей ошибки веса ребер мы суммировали абсолютную разницу между весами ребер в истинной сети и оцененной сети. В целом, меньшая общая ошибка веса ребер указывает на более точную оценку. Во-вторых, мы использовали меры исхода чувствительность (т.е. доля истинных присутствующих ребер, корректно оцененных) и специфичность (т.е. доля истинных отсутствующих ребер, корректно оцененных как ноль) для оценки производительности выбора модели (в случае оценки eLasso) и пороговой обработки значимости (в других оценщиках). В целом, более высокая чувствительность указывает на большую мощность для обнаружения истинных ребер, а высокая специфичность указывает на низкий уровень ложноположительных результатов. В идеале чувствительность увеличивается с размером выборки, а специфичность высока независимо от размера выборки и фиксирована на уровне (1-α) при использовании пороговой обработки значимости. Наконец, поскольку смещение в нашем симуляционном сценарии обычно направлено на отрицательные ребра (например, De Ron et al., 2021), мы изучили долю ложноотрицательных ребер. Эта мера является дополнением к мере чувствительности. Если оценивается отрицательное ребро там, где в истинной сети есть положительное ребро, чувствительность все равно будет увеличиваться (поскольку чувствительность не зависит от знака ребра), но это также увеличит долю ложноотрицательных ребер.

Результаты

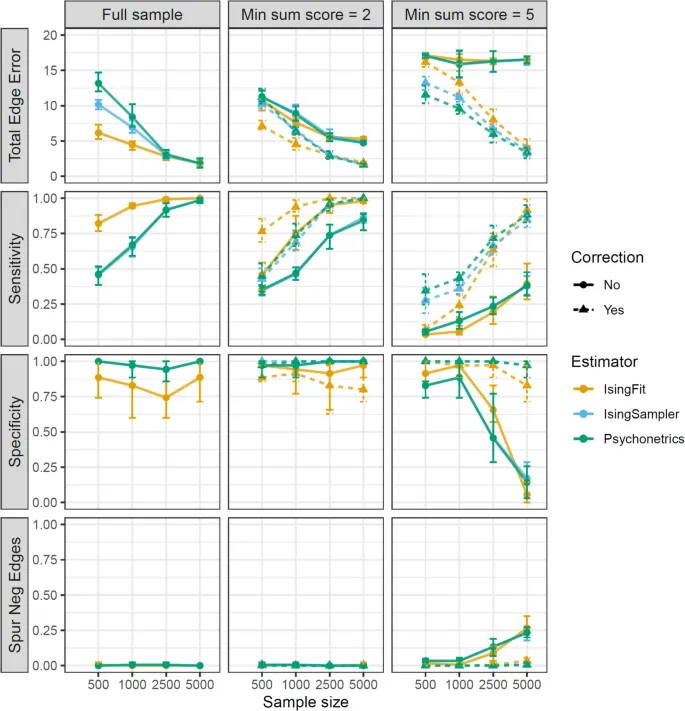
Рис. 3 показывает результаты симуляции 100 прогонов с различными размерами выборки и критериями отсечения суммы баллов. Приложение B (Рис. 6) показывает, что результаты для общей ошибки веса ребер аналогичны, когда мы не используем никакой выбор модели. В каждом условии, где мы использовали критерий суммы баллов, скорректированные сети демонстрируют меньшую общую ошибку веса ребер, чем нескорректированные сети. Когда критерий суммы баллов высок (т.е. ≥ 5), разница между скорректированными и нескорректированными сетями увеличивается с размером выборки: сети, оцененные с помощью коррекции, значительно улучшаются с увеличением размера выборки, тогда как общая ошибка веса ребер остается высокой для сетей, оцененных без коррекции. Это предполагает, что общая ошибка веса ребер в основном обусловлена вариацией выборки для скорректированных сетей и в основном обусловлена смещением для нескорректированных сетей.

Чувствительность и специфичность выше для скорректированных сетей, чем для нескорректированных, и эта разница увеличивается с размером выборки и критерием суммы баллов. С увеличением размера выборки скорректированные сети демонстрируют сильное увеличение чувствительности, тогда как нескорректированные сети показывают лишь небольшое увеличение чувствительности при больших размерах выборки. Более того, при критерии суммы баллов 5 это увеличение для нескорректированных сетей, вероятно, частично связано с включением ложноотрицательных ребер, поскольку доля ложноотрицательных ребер показывает аналогичное увеличение, как и чувствительность для нескорректированных сетей. Специфичность снижается с размером выборки, особенно при критерии суммы баллов 5 и для нескорректированных сетей. Для скорректированных сетей специфичность остается близкой к 1 для всех размеров выборки. Исключением является IsingFit, где специфичность постоянно ниже 1 даже при оценке сети на основе полной выборки. Низкая средняя специфичность, вероятно, связана с тем, что в истинной сети отсутствует всего семь ребер, поэтому оценка одного или двух из этих ребер уже приводит к значительному снижению специфичности. В отличие от других пакетов, IsingFit не использует α = 0,01, что может объяснить, почему этот пакет обнаруживает больше ложноположительных ребер.

Эмпирический пример

В этом примере мы показываем, как наша коррекция может быть использована для проверки гипотезы о наличии по крайней мере двух латентных популяций, тесно связанных с суммой баллов (сценарий 2, описанный во введении). Сначала мы покажем на симулированных данных, как наша коррекция может отвергнуть эту гипотезу. Затем мы покажем пример с эмпирическими данными, который кажется соответствующим этой гипотезе. Однако мы предостерегаем от интерпретации результатов такого типа анализа как доказательства существования латентных популяций, связанных с суммой баллов. Это связано с тем, что другие модели могли бы дать аналогичные результаты. Например, однородная модель Изинга, в которой параметры модерируются суммой баллов, может привести к тем же результатам в сетевом анализе, что и наличие двух различных латентных популяций.

Мы сосредоточимся на сценарии 2, потому что ожидаем, что наиболее вероятной причиной использования исследователями отбора по сумме баллов является подозрение на наличие различных латентных популяций, например, популяции с устойчивой сетевой структурой и популяции с уязвимой сетевой структурой (Borsboom & Cramer, 2013). Поскольку эти латентные популяции не могут быть непосредственно наблюдаемы, мы можем использовать сумму баллов в качестве способа исключения из анализа людей с устойчивой сетью, предполагая, что у людей с устойчивой сетью будет очень низкая вероятность достижения высокой суммы баллов. Следовательно, мы можем использовать сумму баллов как прокси для идентификации латентных популяций.

Симулированный случай

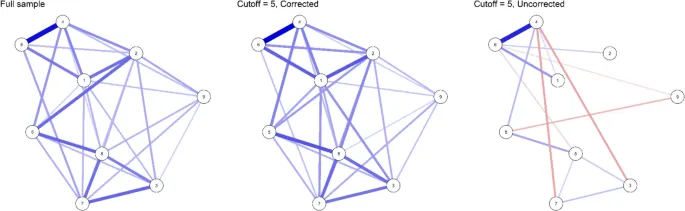
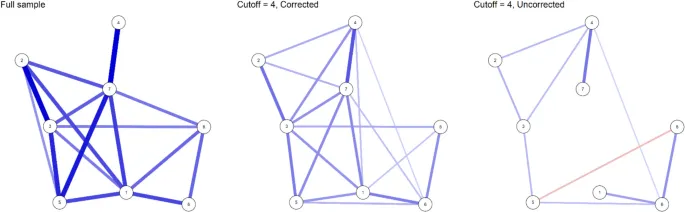
Мы использовали ту же сеть, что и в нашем симуляционном исследовании (Рис. 3), для генерации двух наборов данных с размером выборки 5000. Первый набор данных не имел ограничений по сумме баллов, а второй набор данных состоял только из случаев, где сумма баллов составляла не менее 5. Затем мы оценили три сети: одну на выборке со всеми возможными суммами баллов (далее — сеть полной выборки), одну с нашей коррекцией на выборке, отобранной по критерию суммы баллов (далее — скорректированная сеть), и одну с обычной оценкой на выборке, отобранной по критерию суммы баллов (далее — нескорректированная сеть). Полученные сети показаны на Рис. 4.

Если бы мы обнаружили результаты на Рис. 4 в эмпирическом сетевом анализе, мы могли бы предварительно сделать несколько выводов из визуального осмотра трех сетей. Во-первых, сеть полной выборки и скорректированная сеть выглядят почти идентично. Поскольку, по-видимому, нет различий между этими двумя сетями, мы узнаем две вещи о процессе генерации данных: во-первых, мы узнаем, что нет свидетельств модерирующего эффекта суммы баллов на параметры модели Изинга: параметры одинаковы для всей выборки независимо от суммы баллов. Более того, из этого следует, что не может быть двух или более различных латентных популяций, которые сильно связаны с суммой баллов и различаются по своей сетевой структуре, т.е. параметрам модели Изинга. Если бы мы сравнивали нескорректированную сеть с сетью полной выборки, мы могли бы ошибочно прийти к противоположным выводам, поскольку сети выглядят совершенно по-разному: есть свидетельства либо модерирующего эффекта суммы баллов, либо наличия различных субпопуляций. Однако важно понимать, что различия между нескорректированной сетью и сетью полной выборки вызваны кондиционированием на общий эффект переменных (смещение выборки или смещение Берксона). Следовательно, нескорректированная сеть не может предоставить доказательств в пользу или против модерирующего эффекта суммы баллов или наличия различных субпопуляций в данных (аналогично: Haslbeck et al., 2021b).

Эмпирический случай

Для примера с эмпирическими данными мы использовали данные National Comorbidity Screening Replication (NCSR; Kessler & Merikangas, 2004). Эти данные (N = 9282) содержат данные интервью о наличии или отсутствии девяти симптомов большого депрессивного эпизода (БДЭ) и девяти симптомов генерализованного тревожного расстройства (ГТР) из DSMIV (American Psychiatric Association, 1994). Для нашего примера мы использовали только данные о симптомах БДЭ. Интервью имели пропускную структуру, в которой другие симптомы оценивались только в случае наличия «подавленного настроения» или «потери интереса», а не оцененные симптомы записывались как отсутствующие (0) в окончательных данных (см. Kessler & Merikangas, 2004, для подробностей). Эти данные ранее анализировались Borsboom и Cramer (2013) и Forbes et al. (2017; см. также Borsboom et al., 2017). Из-за пропускной структуры мы решили исключить симптом подавленного настроения из эмпирического примера, поскольку пропускная структура вызывает отрицательную ассоциацию между подавленным настроением и потерей интереса, что не является результатом простого критерия суммы баллов для данных в целом, и поэтому наша коррекция не может это учесть. Более того, было очень мало случаев, когда этот симптом отсутствовал при наличии любого другого симптома (N = 37). Эта проблема была менее выражена для симптома потери интереса, где все еще было 358 случаев, когда симптом отсутствовал при наличии любого другого симптома (исключая подавленное настроение).

Из данных NSCR мы снова оценили три сети: одну сеть, используя данные без ограничений на сумму баллов, одну сеть, используя только данные людей с суммой баллов не менее 4 с нашей коррекцией, и одну сеть людей с суммой баллов не менее 4 при обычной оценке. При оценке сети без ограничений на сумму баллов мы все еще использовали тот же размер выборки, что и для других сетей (N = 2052), путем случайного отбора случаев, чтобы различия в размере выборки не влияли на наши результаты. Полученные сети показаны на Рис. 5.

Мы отмечаем несколько различий между сетью полной выборки и скорректированной сетью: средняя сила ребра кажется выше в полной выборке, чем в скорректированных сетях. Кроме того, в скорректированной сети отсутствуют ребра, которые присутствуют в сети полной выборки, и наоборот. Ребра, отсутствующие в скорректированной сети, могут отсутствовать из-за снижения чувствительности. Наше симуляционное исследование показало, что более высокий критерий отсечения суммы баллов все еще приводил к снижению чувствительности по сравнению с оценкой на полной выборке, вероятно, в результате меньшей вариативности переменных после отбора по сумме баллов. Однако маловероятно, что ребра в полной выборке, присутствующие в скорректированной сети, являются ложными срабатываниями, поскольку мы используем фиксированную частоту ложных срабатываний 0,01.

Наблюдаемые различия предполагают один из двух механизмов, лежащих в основе данных. Во-первых, возможно, что существует одна модель Изинга, которая породила данные, но параметры модели Изинга модерируются суммой баллов симптомов. Модель, для которой такая модерация может наблюдаться, будет расширением модели Изинга с взаимодействием более высокого порядка, чем 2. Второй вариант заключается в том, что в данных существуют субпопуляции, имеющие различную сетевую структуру, т.е. модель Изинга, и они определяются латентным признаком, который тесно связан с суммой баллов. Таким образом, наш метод оценки предоставляет предварительные доказательства того, что одна из этих двух гипотез верна, но не может их различить. Если исследователь имел гипотезу о наличии двух или более субпопуляций с различными моделями Изинга в данных (например, устойчивой и уязвимой субпопуляций), то вывод, который он мог бы сделать, заключается в том, что данные совместимы с этой гипотезой, но не подтверждают ее. Что касается нескорректированной сети, то она снова просто показывает, что мы сместили условные ассоциации между переменными в сторону отрицательных, поскольку присутствующие ребра слабее, чем в других сетях, сеть более разрежена, и присутствует отрицательное ребро.

Обсуждение

Мы представили способ коррекции смещения, возникающего при отборе по сумме баллов в бинарных данных, моделируемых моделью Изинга. Мы предвидим применение наших коррекций в двух сценариях. В первом сценарии объектом вывода является полная популяция, независимо от суммы ее баллов, но данные доступны только для части популяции, отобранной по критерию отсечения суммы баллов. Второй сценарий — когда исследователь подозревает наличие двух латентных субпопуляций, описываемых различными моделями Изинга и неидеально разделяемых критерием отсечения суммы баллов. Хотя никогда нельзя знать, действительно ли имеет место вторая ситуация, мы показали в эмпирическом примере, что наша коррекция может быть использована для демонстрации того, что данные совместимы с наличием нескольких латентных субпопуляций, тесно связанных с суммой баллов. Важно отметить, что даже вне этих двух сценариев сети, оцененные на данных, отобранных на основе суммы баллов без коррекции, не следует использовать для выводов о причинно-следственных связях, поскольку результирующие ассоциации, вероятно, искажены процедурой отбора. Наши результаты симуляции демонстрируют, что предложенный метод коррекции может эффективно снизить смещение выборки после отбора по сумме баллов.

При использовании отбора по сумме баллов в целом и предложенной коррекции в частности следует учитывать несколько аспектов. Первое соображение заключается в том, что коррекция менее эффективна, если используется меньшая подвыборка из исходных данных (т.е. если выбран более высокий критерий отсечения). Это очевидно в случае, когда отсечение является максимальной возможной суммой баллов. Однако даже в менее экстремальных случаях наша симуляция показала, что более высокий критерий отсечения приводит к худшим оценкам параметров, особенно в терминах чувствительности. Это, вероятно, связано с тем, что модель становится труднее оценивать при очень низкой вариативности. Хотя проблема недостаточной вариативности переменной не ограничивается ситуациями, когда используется разделение по сумме баллов, разделение по сумме баллов делает недостаток вариативности более вероятным, поскольку используется меньше данных. Кроме того, многие психические расстройства требуют для диагностики не только достижения определенной суммы баллов симптомов, но и наличия одного из ключевых симптомов. Например, DSM5 требует наличия симптома подавленного настроения или потери интереса для диагностики большого депрессивного расстройства (БДР; American Psychiatry Association, 2013). Эти симптомы почти всегда будут присутствовать в случаях из диагностированной выборки. Вероятно, потребуется очень большой размер выборки, чтобы получить достаточную вариативность в этих симптомах для оценки сети. Если вариативность отсутствует или слишком низка в переменной, невозможно подогнать логистическую регрессию с этой переменной в качестве исхода, что означает, что полную сетевую модель невозможно оценить. Может быть собрана порядковая (ordinal) информация, чтобы избежать проблемы недостаточной вариативности данных, поскольку она естественным образом имеет большую вариативность. Для порядковых данных оценка гауссовской графической модели (GGM; Lauritzen, 1996) является популярным подходом для построения сети (Epskamp & Fried, 2018), хотя эта практика не лишена ограничений (см. Liddell & Kruschke, 2018). Однако неясно, может ли решение, используемое в данном исследовании, быть легко применено при оценке GGM. Хотя GGM имеет известную и управляемую функцию разбиения, наша коррекция опирается на ограничение возможных реализаций при вычислении нормализующей константы, что нелегко реализовать в непрерывной GGM. Будущие исследования могли бы изучить способы коррекции смещения выборки при оценке GGM или порядковых моделей, как предложено в Marsman et al. (2025).

Второе соображение заключается в том, что если исследователи используют нашу коррекцию для оценки гипотезы о наличии нескольких субпопуляций, связанных с суммой баллов, которые имеют различные модели Изинга, предложенный метод не может предоставить доказательств в пользу этой гипотезы, как обсуждалось в разд. 4. Более прямой подход к ответу на этот вопрос заключался бы в использовании анализа латентных классов (LCA; например, Weller et al., 2020) или для непрерывных данных — смешанного моделирования (например, McLachlan et al., 2019), поскольку это позволяет исследователю напрямую проверить существование различных субпопуляций в данных. Однако основным ограничением такого типа анализа в отношении проверки этой гипотезы является то, что большинство пакетов программ для подгонки LCA предполагают независимость переменных внутри различных классов, что соответствует пустым моделям Изинга. Следовательно, традиционный анализ латентных классов не подходит для ситуации, когда латентные классы определяются различными моделями Изинга. Поэтому для прямой оценки наличия субпопуляций с различными моделями Изинга нам требуется комбинация LCA и сетевого анализа, в которой из данных могут быть извлечены латентные классы различных сетевых моделей, что также было определено как направление для будущих исследований в Haslbeck et al. (2023).

Наконец, мы хотели бы подчеркнуть, что по-прежнему жизненно важно, чтобы исследователи тщательно обдумывали причину, по которой они хотят разделить данные по сумме баллов. Например, часто предполагалось, что симптоматические сети людей с расстройством демонстрируют большую связанность, чем у людей без расстройства (Van Borkulo et al., 2015; Cramer et al., 2016; Colli et al., 2024; будет ли эта гипотеза верна: Hoekstra et al., 2024). Однако отбор данных с критерием отсечения суммы баллов в кросс-секционном наборе данных, как это сделано в данном исследовании, может быть неоптимальным способом для его изучения. Кросс-секционные сети показывают эффекты, существующие между людьми в выборке, а не процессы внутри людей в выборке (Borsboom et al., 2021; Hamaker et al., 2015). Если гипотеза заключается в том, что сильная связанность между симптомами на индивидуальном уровне представляет высокий риск развития психического расстройства, эта сильная связанность не обязательно будет обнаружена на уровне выборки. Таким образом, для изучения уязвимости сети представляется более целесообразным рассматривать временные сетевые модели, поскольку они могут выявлять внутриличностные процессы (обзор моделей представлен в Borsboom et al., 2021; Epskamp et al., 2018b). Однако даже при изучении внутриличностных сетей остается под вопросом, будут ли обнаружены различия в связанности с использованием текущих методов моделирования (для более подробной информации см. Hoekstra et al., 2024). Наконец, если единственная причина для сетевого анализа после разделения по сумме баллов заключается в том, чтобы увидеть, существуют ли качественные различия между людьми с психическим расстройством и без него, это также можно проверить с помощью анализа латентных классов, если предполагаемое различие заключается не только в сетевой структуре (Haslbeck et al., 2021b; Weller et al., 2020).

В итоге, мы представили метод, который эффективно корректирует смещение после отбора по сумме баллов, и предоставляем реализации в IsingFit, IsingSampler, psychonetrics и bootnet. Благодаря этим реализациям наш метод может быть легко использован исследователями. Поскольку отбор по сумме баллов является распространенным явлением в психологических исследованиях, особенно при изучении условных ассоциаций между симптомами психического расстройства, наш метод может стать ценным дополнением к этой области.