Нелинейная модель диффузии для анализа принятия решений: учет эндогенных эффектов

Введение в моделирование процессов принятия решений

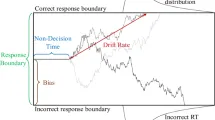
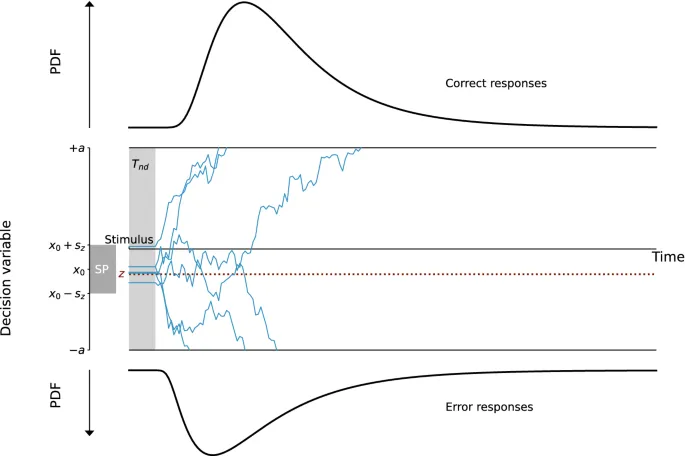
Перцептивное принятие решений изучалось extensively с поведенческой и нейрофизиологической точек зрения, поскольку этот процесс повсеместно присутствует в повседневной деятельности. Когда решения принимаются в условиях временных ограничений, модели накопления доказательств точно описывают поведение человека и животных. Они предполагают, что решения принимаются, когда собрано достаточное количество сенсорных доказательств.

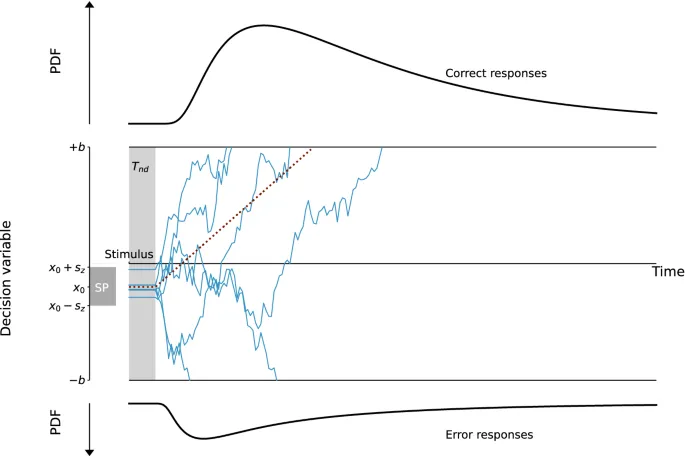
Среди этих моделей, Модель Диффузионного Решения (DDM, также называемая Моделью Дрейфа-Диффузии) предполагает, что доказательства накапливаются линейно, с постоянным дрейфом. Накопление дополнительно подвержено гауссовскому шуму; следовательно, состояние принятия решения можно рассматривать как частицу, следующую броуновскому движению. Популярность этой модели обусловлена ее интуитивно понятным формализмом и хорошим соответствием поведенческим и нейрофизиологическим данным. Также было показано, что DDM формализует оптимальную стратегию для принятия решений в условиях временных ограничений. Интересно, что другие формы моделей принятия решений, такие как модель Протекающего-Конкурирующего Накопителя и модели аттракторов, могут быть сформулированы эквивалентно DDM при определенных ограничениях.

Ограничения классической модели DDM

DDM учитывает глобальную статистику поведения, описывая распределение времени реакции (RT) и частоту ошибок. Основное ограничение этой модели заключается в том, что она не учитывает межпробную изменчивость. Однако поведенческие исследования показали, что последовательные эффекты влияют на prior expectations и последующий процесс принятия решений. Традиционно ожидания моделируются через начальную точку или смещение процесса накопления. Недавние исследования предположили, что история выбора влияет на последующие скорости дрейфа. Вместе эти исследования предполагают, что эти параметры могут быть переплетены и варьироваться во времени, по мере того как участники становятся более familiar с задачей.

Линейное накопление доказательств также предполагает, что накопление доказательств не зависит от состояния решения или от проходящего времени. Хотя некоторые модели учитывают влияние времени на решение или динамику вблизи порога, ни одна модель, насколько нам известно, не учитывает начальную динамику. Например, неоднозначные стимулы могут приводить к плоским начальным дрейфам. Это частично translated into non-decision time, так как предполагается, что это время, когда сенсорная информация обрабатывается в мозге, не contributing to процессу принятия решений.

Предлагаемое решение: нелинейная модель диффузии (nlDDM)

Здесь мы предлагаем простую одномерную нелинейную форму для решения этих ограничений: нелинейная Модель Дрейфа-Диффузии (nlDDM). Она воссоздает dynamics типа "двойной ямы" с точки зрения накопления доказательств без assumption симметрии отражения. Мы показываем ее валидность и сравниваем ее производительность fitting с таковой у DDM. Сначала мы предоставляем формальное описание nlDDM, связывая ее с DDM. Затем мы подгоняем модели на двух наборах данных о поведении человека: задаче лексической классификации, уже опубликованной, и задаче мультисенсорной классификации.

Формализм nlDDM

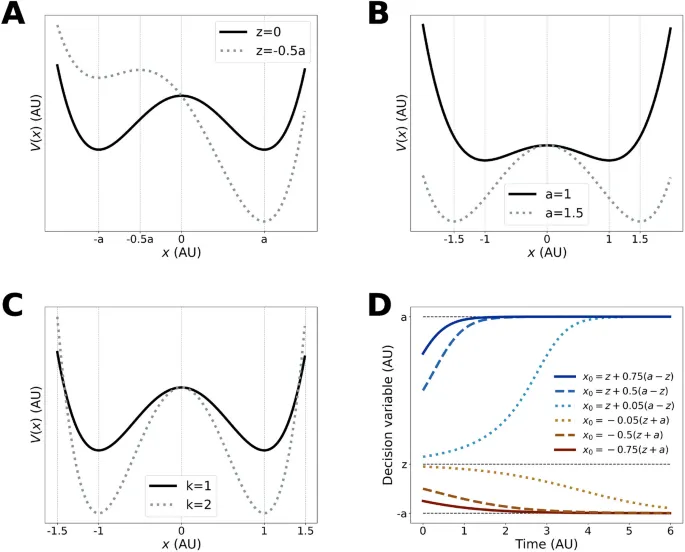
Наша цель состояла в том, чтобы предложить простую модель, в которой trajectories притягиваются к границе. Помещая себя в контекст paradigms выбора из двух альтернатив, наша модель нуждалась в двух attractive состояниях. В одном измерении это forces существование unstable фиксированной точки между двумя stable фиксированными точками.

Следовательно, модель, которую мы предлагаем, следует уравнению Ланжевена, где дрейф изменяется с состоянием решения. Уравнение дрейфа можно записать в следующей форме: dx = k(x+a)(x-z)(x-a)dt + N(t), где x представляет переменную решения, а dx - ее изменение в бесконечно малом времени dt. N(t) - это гауссовский белый шум. k(x+a)(x-z)(x-a) представляет дрейф и зависит от нескольких параметров. Параметр k является time constant системы, а a и z определяют, где лежат аттракторы, или границы решений. ±a представляют два attractive состояния, и мы ограничиваем z интервалом ]-a, a[, чтобы получить z - unstable фиксированную точку.

Интерпретация параметров модели

Интерпретация k как постоянной времени straightforward из уравнения: по мере увеличения k решение достигается быстрее для любого заданного набора параметров.

Чтобы построить интуицию для других параметров, мы сначала рассматриваем potential function, полученную из члена дрейфа. Этот профиль называется профилем потенциала двойной ямы. Из него мы можем видеть, что есть два стока в ±a, а также источник в z, которые emerge из топологии системы. Следовательно, ±a являются границами решений и контролируют, наряду с z, компромисс между скоростью и точностью.

Подобно DDM, мы можем подогнать RTs, решив уравнение Фоккера-Планка, соответствующее уравнению Ланжевена. Затем, non-decision time T_nd сдвигает resulting distribution и учитывает биологические transmission delays.

Производительность модели и сравнения

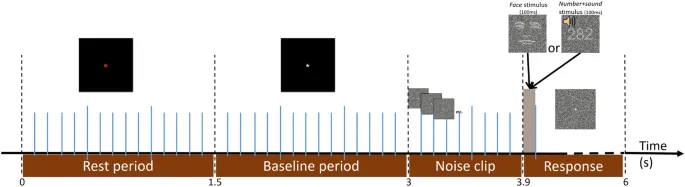
Мы протестировали качество nlDDM, подгоняя ее к данным, которые мы собрали. 25 здоровых участников с нормальным или скорректированным зрением и слухом приняли участие в эксперименте по перцепционной классификации. Участникам на каждом trial предъявлялись изображения лиц или изображения чисел, и они должны были respond с помощью щелчков мыши, чтобы report, какой стимул они perceived.

Поведенческие результаты

В среднем участникам показывали 49.82 ± 2.42% стимулов "число+звук", что указывает на квазиравновероятность каждого стимула. Затем мы выполнили mixed-model ANOVAs на их RTs и точности ответов для обоих stimulus-response mapping (межсубъектный фактор) и стимула (внутрисубъектный фактор). По всем участникам и типам стимулов среднее RT составило 535 ± 61 мс с точностью 98.59 ± 0.95%.

Сравнение значений потерь

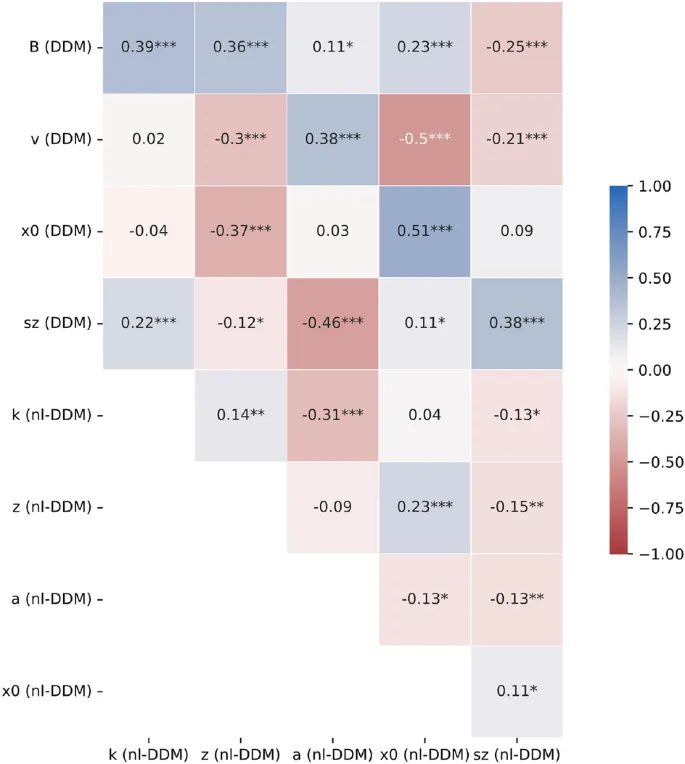
Подгонка параметров выполнялась с использованием PyDDM для both nlDDM и DDM, минимизируя negative log-likelihood function. Мы подогнали модель на каждого участника и тип модели, получив 25 DDM и 25 nlDDM на наборе данных сенсорной классификации. DDM был подобран с использованием 6 параметров, а nlDDM состоял из 7 параметров.

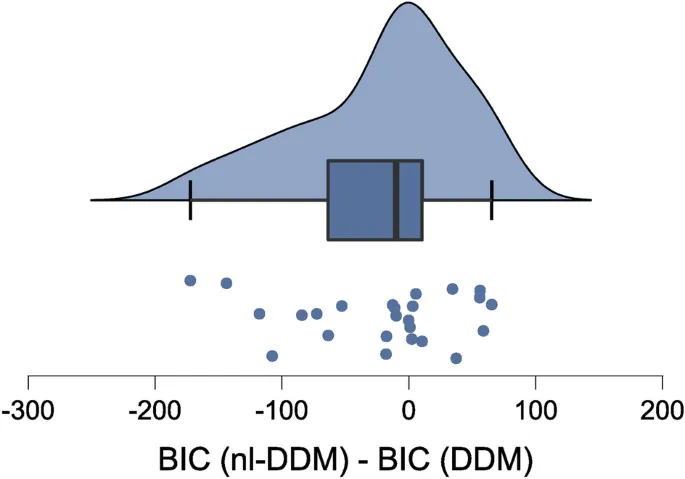
Мы вычислили Bayesian Information Criterion (BIC) для каждой модели, подобранной на мультисенсорном наборе данных, чтобы установить сравнение производительности модели, которое учитывает размер выборки и количество параметров для каждой модели. Мы наблюдали, что nlDDM подогнал данные RT significantly лучше, чем DDM, даже при учете количества параметров.

Влияние passage времени

Время, затраченное на выполнение задачи, likely impact стратегию принятия решений, и мы стремимся смоделировать эти эффекты с помощью DDM и nlDDM. Таким образом, мы добавили time condition к набору данных лексической классификации, соответствующее тому, был ли trial выполнен в первой половине эксперимента (условие "early") или во второй ("late").

Подгонка модели для временного анализа

Дрейф и z DDM и nlDDM варьировались в зависимости от сложности стимула (common, rare, very rare, nonexistent word), а граница DDM варьировалась в зависимости от both инструкции (speed/accuracy) и временного условия, resulting in 4 boundaries. В nlDDM эффекты моделировались separately с использованием a и k, подгоняя k в зависимости от временного условия и a в соответствии с инструкцией.

Мы сравнили производительность подгонки двух моделей. BIC nlDDM был significantly меньше, чем BIC, полученный DDM, что подтверждает необходимость учета времени эксперимента.

Обсуждение и выводы

В этой статье мы представили нелинейную Модель Дрейфа-Диффузии (nlDDM) и показали, что она работает лучше, чем DDM, с точки зрения точности подгонки поведения. Модель обеспечивает framework для более refined анализов процесса принятия решений и учитывает влияние времени эксперимента на поведение.

Наша модель открывает путь к более точному анализу межпробной изменчивости для перцепционных решений и учитывает peri-stimulus влияния. Мы предоставляем open-source код, pluggable onto инструментарий PyDDM для reproducibility и easy use нашей модели.