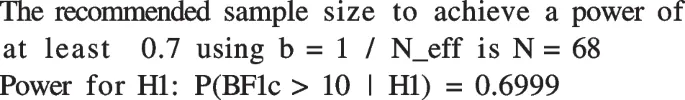Определение размера выборки в байесовском анализе для продольных исследований

Введение

Важной частью планирования эксперимента является определение необходимого размера выборки для достижения желаемого уровня статистической мощности. Мощность — это вероятность обнаружения существующего эффекта, что эквивалентно вероятности не совершить ошибку II рода (ложноотрицательный результат). Ошибка II рода возникает, когда ошибочно делается вывод об отсутствии эффекта. Мощность исследования зависит от размера выборки, величины эффекта и вероятности совершения ошибки I рода (ложноположительный результат). Исследователи стремятся к высокой мощности, чтобы увеличить шансы обнаружения существующего эффекта, и часто ищут размер выборки, необходимый для достижения желаемого уровня мощности. Этот процесс называется «определением размера выборки» (SSD) и требуется большинством этических комитетов и финансирующих организаций.

Преимущества определения размера выборки

• Избегание недооцененных исследований, где эффект существует, но не обнаруживается из-за малого размера выборки.
• Предотвращение переоцененных исследований с избыточно большими выборками, что приводит к неэффективному использованию ресурсов.

Байесовский подход к проверке гипотез

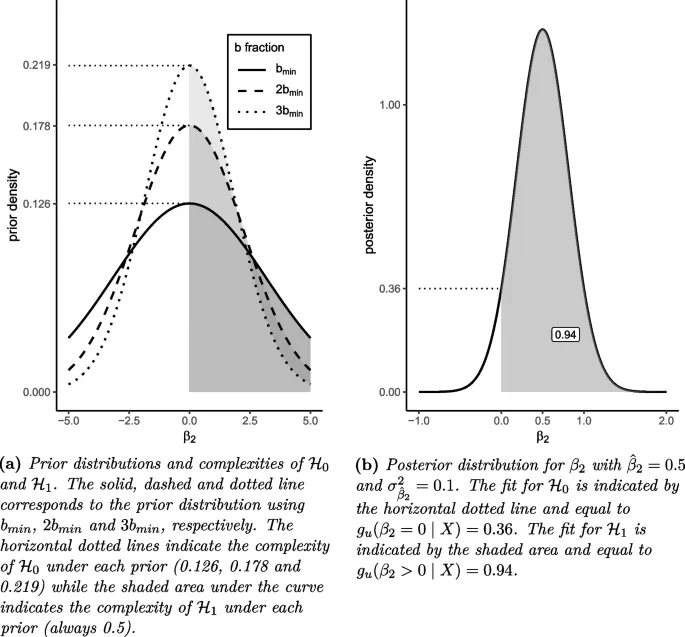
В отличие от частотного подхода к проверке гипотез (NHST) с использованием p-значений, байесовский анализ использует байесовский фактор (BF) как альтернативный инструмент вывода. BF позволяет сравнивать относительную поддержку данных для конкурирующих гипотез. Однако некоторые исследователи все еще сомневаются в использовании байесовских методов из-за их кажущейся сложности. Для решения этой проблемы мы используем приближенный скорректированный дробный байесовский фактор (AAFBF), который оценивает пару конкурирующих гипотез на основе оценок максимального правдоподобия из частотных моделей.

Преимущества байесовского фактора

• Интуитивная интерпретация: BF показывает, во сколько раз данные поддерживают одну гипотезу по сравнению с другой.
• Возможность получения доказательств в пользу нулевой гипотезы, что невозможно в частотном подходе.
• Отсутствие зависимости от размера выборки при интерпретации результатов.

Многоуровневые модели для продольных данных

В психологических исследованиях часто используются многоуровневые модели, особенно при работе с продольными данными. Эти модели учитывают вложенность наблюдений внутри индивидов, что делает их более гибкими по сравнению с традиционными методами, такими как ANOVA. Многоуровневые модели позволяют:

• Учитывать корреляцию между измерениями внутри одного индивида.
• Работать с неравномерно распределенными временными точками.
• Минимизировать потерю данных при наличии пропущенных значений.

Двухуровневая модель для продольных исследований

Рассмотрим продольный набор данных, состоящий из N индивидов с n измерениями каждый. Групповая принадлежность обозначается бинарной переменной C_i. На первом уровне (внутри индивида) модель определяется уравнением регрессии:

Y_ij = π_0i + π_1i T_j + e_ij, где e_ij ∼ N(0, σ²)

На втором уровне (между индивидами) коэффициенты моделируются как:

π_0i = β_0 + u_0i

π_1i = β_1 + β_2 C_i + u_1i

Определение размера выборки в байесовском подходе

Для выполнения SSD в байесовском подходе необходимо:

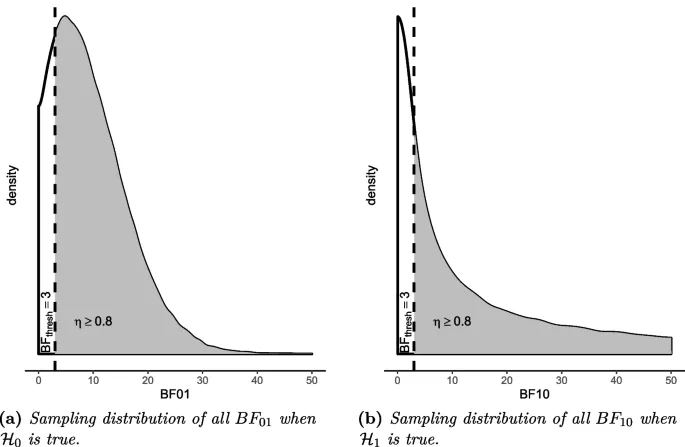
1. Определить пороговое значение BF (BF_thres), которое считается убедительным доказательством.
2. Установить желаемый уровень мощности η, который отражает вероятность получения BF, превышающего BF_thres, в пользу истинной гипотезы.

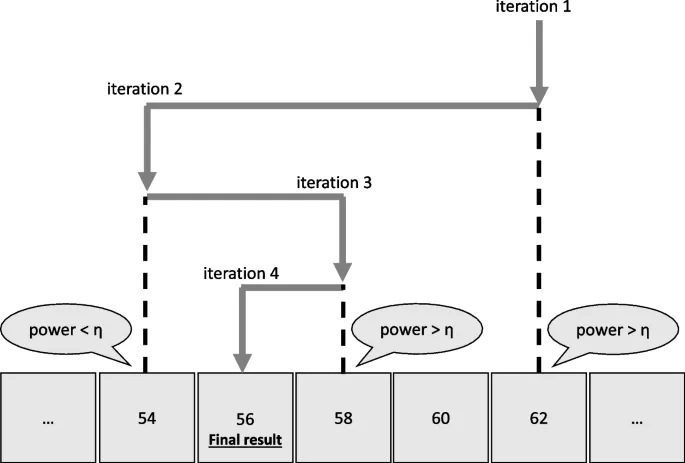
Алгоритм BayeSSD использует метод бинарного поиска для определения минимального размера выборки, удовлетворяющего условиям мощности. Результаты выводятся для разных значений параметра b (доля данных, используемых для построения априорного распределения).

Примеры применения

В статье приведены два примера применения метода:

• Линейный рост с равномерно распределенными временными точками (на примере исследования антисоциального мышления у подростков).
• Логлинейный рост с неравномерно распределенными временными точками (на примере исследования систематической обратной связи в психотерапии).

Заключение

Представленный метод позволяет исследователям оптимизировать дизайн продольных исследований с использованием байесовского подхода. Функция BayeSSD доступна в открытом доступе на GitHub и может быть использована для обоснования размера выборки в заявках на финансирование и этическое одобрение. В будущих исследованиях планируется расширить функциональность метода, включив поддержку большего числа гипотез и учет выбывания участников.