Асимметричное обучение и адаптация к изменениям в иерархиях

Введение

Люди легко обучаются ранжированию объектов по различным скрытым шкалам, таким как гедонистическая или экономическая ценность, или социальное влияние. Такие представления о ранжировании позволяют делать новые выводы о косвенно связанных состояниях или сущностях. Например, знание того, что A > B и B > C, позволяет вывести, что A > C.

Поведенческие модели

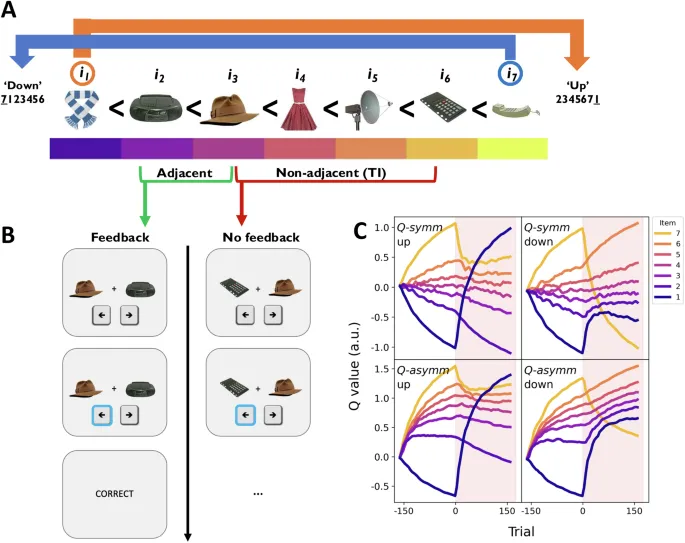
Согласно Ciranka et al.5, мы моделировали реляционное обучение в нашей парадигме транзитивного умозаключения (ТИ) с использованием простых моделей обучения с подкреплением (RL), которые обновляли оценки ценности (т. е. «нарциссизма») Q выигрышных и проигрышных элементов x и y соответственно, после обратной связи о выборе по модифицированному правилу обновления Rescorla-Wagner28:

$$Q_{t+1}(x) = Q_t(x) + lpha^+ [1 - d_t(x,y)Q_t(x)]$$ (1)

$$Q_{t+1}(y) = Q_t(y) + lpha^- [1 + d_t(x,y)Q_t(y)]$$ (2)

где α⁺ и α⁻ — скорости обучения для победителей и проигравших соответственно. Разделение этих скоростей обучения позволило модели реализовать различную степень симметрии/асимметрии в своих обновлениях обучения. Мы определили симметричную модель Q_symm как агента, для которого α⁺ = α⁻, что означает, что исходы выбора увеличивали и уменьшали оценки ценности агента для победителей и проигравших на одинаковую величину. В отличие от этого, мы определили асимметричную модель Q_asymm как агента, чьи скорости обучения α⁺ и α⁻ могли свободно варьироваться. В случае, когда α⁺ > α⁻, агент был «склонным к победителям», непропорционально увеличивая свою оценку ценности победителя сравнения относительно его проигравшего, в то время как агент был «склонным к проигравшим», если α⁺ < α⁻. Формальный параметр d_t(x,y) определяет, является ли обратная связь положительной (+1) или отрицательной (-1) относительно ожидания агента (т. е. Q(x) > Q(y)).

Предполагая, что Q(x) > Q(y), положительная обратная связь (1) о том, что x > y, должна привести к меньшему изменению оценки ценности, чем отрицательная обратная связь (-1), которая противоречит ожиданиям. Аналогично, если Q(x) < Q(y), отрицательная обратная связь (-1) о том, что x > y, должна привести к меньшему изменению оценки ценности, чем положительная обратная связь (1), которая противоречит ожиданиям. Принцип, лежащий в основе этих уравнений, заключается в том, что информация, которая подтверждает ожидания агента, обрабатывается менее интенсивно, чем информация, которая им противоречит. Это отражает общую тенденцию к предвзятости подтверждения, когда люди склонны придавать больший вес информации, которая соответствует их существующим убеждениям.

Выбор между элементами x и y осуществлялся на основе разницы между оцененными значениями элементов:

$$p_t(x > y) = rac{1}{1 + e^{(Q_t(x) - Q_t(y))/ au }}$$ (5)

где τ — параметр температуры, определяющий форму сигмоидной функции и, следовательно, степень шума в выборе на основе разницы в ценности элементов. Отметим, что Ciranka et al.5 обнаружили, что включение дополнительного компонента обучения на уровне пар, который позволял эпизодически обучаться парам, для которых была предоставлена обратная связь, улучшало соответствие модели, захватывая усиленное обучение для прямых сравнений соседних элементов. В данном исследовании мы решили опустить этот компонент, чтобы упростить пространство моделей и сосредоточиться конкретно на том, как асимметричное обучение и адаптивность, которую оно обеспечивает, формируют инференционное выполнение по транзитивным иерархиям.

Скорости обучения α⁺ и α⁻ остаются неизменными на протяжении всего эксперимента для Q_symm и Q_asymm. Чтобы проверить, могут ли асимметрии обучения различаться в зависимости от точки изменения, мы ввели Q_asymm2, которая дополнительно обладает отдельной парой скоростей обучения для победителей и проигравших соответственно для фаз до и после точки изменения. Другими словами, модель изначально обучается, используя α⁺_pre, α⁻_pre, прежде чем использовать α⁺_post, α⁻_post после первого изменения. Эта модель позволяет адаптировать асимметрию обучения с течением времени.

Чтобы еще больше учесть, как агенты могут адаптировать степень своей асимметрии обучения, мы ввели модель Q_adapt. В этой модели асимметрия обучения модулируется динамически на основе предпочтения выбора агента, выраженного как p_t(x > y). Модулятор асимметрии λ_t вычисляется следующим образом:

$$ ambda_t = 1 - (1 - mega) eft[ 2(p_t(x > y) - 0.5)^2 ight] $$ (6)

Значение λ минимально, вызывая более симметричное обновление, когда предпочтение выбора агента сильно выражено и, следовательно, четко подтверждается или опровергается получением двоичной обратной связи (т. е. когда p(x > y) приближается к 1 или 0), в то время как оно максимально, вызывая более асимметричное обновление, когда у агента нет предпочтений (т. е. когда p(x > y) = 0.5). ω — дополнительный параметр чувствительности, ограниченный диапазоном от 0 до 1, контролирующий форму квадратичной функции модулятора асимметрии (рис. S5A). Он определяет, насколько легко агент адаптирует степень асимметрии скорости обучения в зависимости от силы предпочтения своего выбора, фактически реализуя квадратичную функцию, которая может быть более пологой или более крутой в зависимости от значения ω. Когда ω = 0, асимметрия агента нечувствительна к изменениям силы предпочтения, так что λ = 1 (т. е. полное асимметричное обновление) для всех вероятностей выбора. Когда ω = 1, Уравнение 6 становится примерно эквивалентным функции энтропии выбора (см. Уравнение 9 в Дополнительной заметке 1). Затем член λ может использоваться для распределения базовой скорости обучения агента α₀ между α⁺_t и α⁻_t:

$$ lpha_{t}^{+} = lpha_0 rac{1 + ambda_t}{2} $$

$$ lpha_{t}^{-} = lpha_0 rac{1 - ambda_t}{2} $$

Хотя α₀ остается постоянным, α⁺_t и α⁻_t изменяются с течением времени в зависимости от λ_t. Важно отметить, что λ_t никогда не бывает отрицательным, поэтому α⁺_t ≥ α⁻_t, если α₀ > 0. Таким образом, α⁺_t может быть больше или равно α⁻_t. Это соответствует недавним эмпирическим работам, не обнаружившим свидетельств адаптивного обращения знака асимметрии обучения человека23,24 (но см. ссылку 25).

Модельное соответствие и сравнение

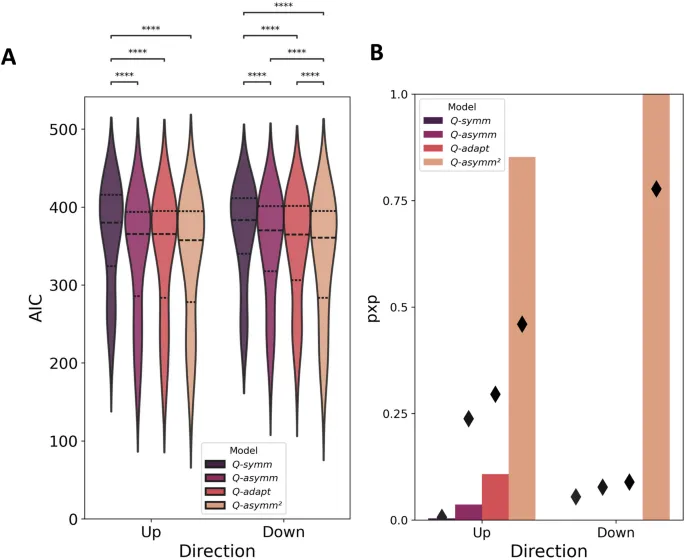
Мы оценили параметры модели, минимизируя отрицательный логарифм правдоподобия однократных ответов каждого участника, учитывая каждую модель. Обратите внимание, что во всех модельных соответствиях и симуляциях мы непосредственно оценивали предсказанные моделью вероятности выбора (Уравнение 5), чтобы избежать ошибки биномиальной выборки, связанной с получением конкретных (двоичных) выборов модели. Мы использовали метод дифференциальной эволюции Scipy29,30 в течение 500 итераций со следующими нижними и верхними границами параметров: α⁺/α⁻: (0; 0.5); α₀: (0.5; 0.5); η: (0; 10); τ: (0; 1). Из полученных значений логарифма правдоподобия при этих наилучших оценках параметров мы вычислили значения информационного критерия Акаике (AIC) как приближение свидетельства модели, где более низкий AIC указывает на лучшее соответствие, одновременно штрафуя за сложность модели31:

$$ AIC = 2 og(p(D|M, at{ heta})) + 2k $$ (9)

Это соответствует правдоподобию данных выбора участника D при данной модели M и ее наилучших параметрах {at{ heta}} плюс штрафной член k, соответствующий количеству свободных параметров. Значения AIC, в свою очередь, использовались для количественной оценки защищенной вероятности превышения (pxp), связанной с каждой конкурирующей моделью, с использованием инструмента вариационного байесовского анализа в MATLAB32. Значения pxp отражают вероятность того, что данная модель лучше соответствует данным участников, чем все другие конкурирующие модели, и, следовательно, является наиболее частой моделью, генерирующей данные в исследуемой популяции. В отличие от метрики вероятности превышения, pxp дополнительно учитывает нулевую гипотезу о том, что нет разницы в частоте каждого типа моделей33.

Чтобы проверить наш подход к сравнению моделей и выводу параметров, мы провели анализ восстановления моделей и параметров, который выявил надежную идентифицируемость наших кандидатных моделей и их подобранных параметров. Детали этого анализа изложены в разделе «Восстановление моделей и параметров» в Дополнительных методах (рис. S4AD и S10AB).

Статистические тесты

Все статистические тесты проводились как двусторонние. Поведенческие эффекты, такие как различия в точности или предпочтении выбора выше случайного, между группами или по точкам изменения, оценивались с помощью t-тестов и ANOVA, для которых мы использовали d Коэна и η_p² в качестве мер размера эффекта соответственно. 95% доверительные интервалы для значений η_p² вычислялись с использованием онлайн-инструмента: https://effectsizecalculator.herokuapp.com/. Предполагалось, что распределение данных является нормальным, хотя это формально не проверялось. В отличие от этого, различия в соответствии моделей тестировались с использованием непараметрических тестов знаковых рангов Уилкоксона, а различия в параметрах моделей тестировались с использованием тестов Манна-Уитни U, из-за ненормального распределения значений AIC и полученных скоростей обучения. Непараметрические размеры эффекта рассчитывались как:

$$ r = rac{z}{qrt{N}} $$ (10)

где z — соответствующий z-статистика непараметрического теста, а N — размер выборки. Для аппроксимации доверительного интервала для размера эффекта каждого непараметрического теста мы использовали бутстрэп-подход с 10 000 выборками. Порог значимости в каждом случае составлял 0.05, и применялась поправка Бонферрони в случаях, когда развертывались апостериорные сравнения (например, для парных t-тестов, используемых после значимых эффектов взаимодействия ANOVA).

Сводка отчетов

Дополнительная информация о дизайне исследования доступна в Сводке отчетов Nature Portfolio, связанной с этой статьей.

Результаты

Симуляции

Сначала мы представляем симуляции симметричного и асимметричного RL-агентов Q_symm и Q_asymm соответственно, чтобы вывести предсказания модели о том, как люди должны вести себя в нашей парадигме ТИ с точкой изменения (рис. 1C и S1). Мы симулировали производительность модели в диапазоне значений параметров, соответствующих тем, которые ранее были оценены для соответствия человеческому поведению ТИ по Ciranka et al.5, где участники имели тенденцию демонстрировать правило обучения, склонное к победителям (т. е. α⁺ > α⁻), при подгонке с Q_asymm. Предпочтительное обновление победителей таким образом приводит к сжатию латентной структуры ценности Q_asymm до точки изменения, так что пары элементов с более высокой ценностью менее различимы, чем пары с более низкой ценностью. Эта сниженная чувствительность к большим значениям является признаком асимметрии в реляционном обучении. В отличие от этого, симметричный агент Q_symm не демонстрирует такого сжатия (подробности см. в ссылке 5).

Интересно, что асимметричное обучение Q_asymm предсказывает разницу в том, насколько эффективно оно должно адаптироваться к нашей манипуляции точкой изменения в «восходящем» условии по сравнению с «нисходящим» условием (рис. 1C и S1). Если обучение склоняется к победителям, точка изменения в «восходящем» условии должна быть легко принята, поскольку Q_asymm выборочно и надлежащим образом увеличивает свою оценку ценности i1, не нуждаясь в обновлении каких-либо других элементов. С другой стороны, в «нисходящем» условии первоначальная тенденция Q_asymm увеличивать свою оценку i1 чрезмерно завышает ценность этого элемента и недооценивает снижение ценности i7. В отличие от этого, пропорциональное обновление победителей и проигравших Q_symm означает, что он будет одинаково эффективно адаптироваться к этим двум объективным изменениям в лежащей в основе истинной структуре. Таким образом, если инференционное обучение характеризуется асимметричным, склоненным к победителям правилом обучения, то это приводит к эмпирическому предсказанию, что люди должны более эффективно адаптироваться к изменению реляционной структуры в «восходящем» условии, чем в «нисходящем».

Сжатие ценности

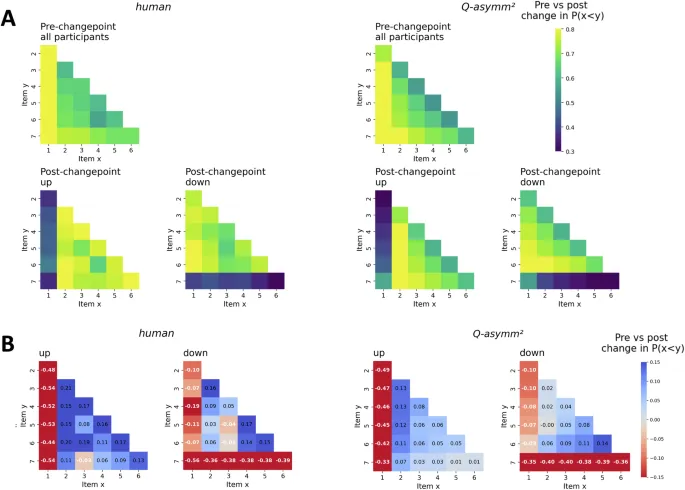
Чтобы проверить эти предсказания модели, мы обратились к эмпирическим данным нашего поведенческого эксперимента. Сосредоточившись сначала на поведении участников до точки изменения (т. е. все испытания, предшествующие первому изменению), мы обнаружили, что, как и предсказывалось, участники демонстрировали сжатую структуру ценности, с наклонами, значительно отличными от нуля, которые были более выражены у «нисходящих» участников (рис. 3A). Это согласуется с предсказаниями модели, что асимметричное обучение приводит к сжатию ценности.

Влияние точки изменения

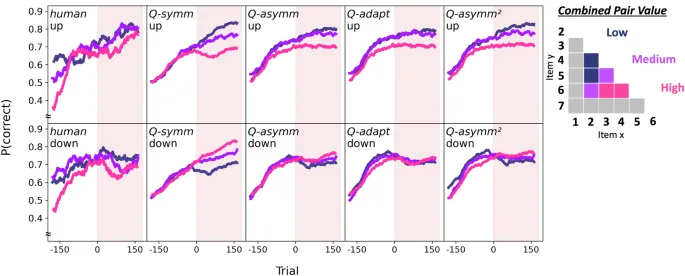
Затем мы рассмотрели влияние точки изменения на производительность ТИ. В «восходящем» условии мы наблюдали значительное улучшение точности ТИ после точки изменения, что соответствует предсказаниям модели о легкой адаптации. В «нисходящем» условии, однако, мы наблюдали значительное снижение точности ТИ после точки изменения, что указывает на более нарушающий эффект. Это различие между условиями согласуется с предсказанием модели, что асимметричное обучение по-разному влияет на адаптацию к изменениям в зависимости от их направления.

Сравнение моделей

Мы сравнили соответствие четырех моделей (Q_symm, Q_asymm, Q_asymm2 и Q_adapt) данным участников. Модель Q_asymm2, которая позволяла асимметрии обучения меняться в точке изменения, показала наилучшее соответствие для «нисходящей» группы, в то время как Q_adapt, которая динамически регулировала асимметрию обучения, показала наилучшее соответствие для «восходящей» группы. Модель Q_symm показала наихудшее соответствие во всех случаях.

Значения pxp (защищенной вероятности превышения) для Q_asymm2 и Q_adapt были высокими для соответствующих групп, что указывает на то, что эти модели лучше всего объясняют данные участников. Например, для «восходящей» группы Q_adapt имела pxp > 0.99, в то время как для «нисходящей» группы Q_asymm2 также имела pxp > 0.99. Обратите внимание, что Q_asymm и Q_symm имели pxp < 0.01. Мы отмечаем, что по байесовскому информационному критерию (BIC), метрике свидетельства модели, которая сильнее штрафует за сложность модели и, следовательно, отдает предпочтение более простым моделям, Q_adapt и Q_asymm2 стали выигрышными моделями в «восходящей» и «нисходящей» группах соответственно, хотя эта метрика привела к худшему восстановлению модели, чем AIC (рис. S4C, D и рис. S6A, B). В совокупности это указывает на то, что Q_asymm2 превзошла как свои статические аналоги Q_symm и Q_asymm, так и более динамически адаптивную модель Q_adapt, особенно в отношении «нисходящих» участников.

Углубленное изучение асимметрии обучения

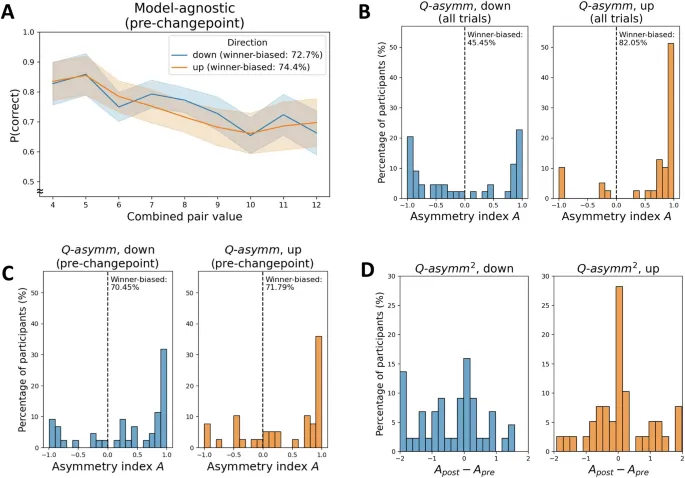
Чтобы глубже изучить характер этого сдвига в скоростях обучения, мы вычислили индексы асимметрии α⁺_pre и α⁻_pre для Q_asymm2, используя каждую из этих пар подогнанных скоростей обучения (рис. 4D). Участники в «восходящей» группе показали предвзятость обучения в пользу победителей в фазе до точки изменения, которая не отличалась существенно между точками изменения (среднее α⁺_pre = 0.42 ± 0.11 SE; среднее α⁻_pre = 0.51 ± 0.10 SE; тест знаковых рангов Уилкоксона: z = 0.35, p = 0.727, r = 0.06, CI = (0.00, 0.38)). Однако участники в «нисходящей» группе претерпели значительное снижение предвзятости обучения в пользу победителей после точки изменения (среднее α⁺_pre = 0.37 ± 0.10 SE; среднее α⁻_pre = -0.02 ± 0.12 SE; тест знаковых рангов Уилкоксона: z = -2.04, p = 0.041, r = -0.31, CI = (-0.56, -0.04)). Анализ этих различий в асимметрии по точкам изменения указал на бимодальное разделение участников на тех, чьи индексы асимметрии оставались стабильными по точкам изменения, т. е. их предвзятость оставалась неизменной, и тех, кто демонстрировал выраженное снижение или даже изменение знака своего индекса асимметрии, т. е. тенденцию к большей симметрии или даже предвзятости к проигравшим (см. рис. 4D).

Соответственно, мы наблюдали, что наилучшие значения параметра адаптивности Q_adapt, ω, были бимодально распределены вокруг 0 и 1 (т. е. соответствуя отсутствию адаптивности и максимальной адаптивности асимметрии обучения соответственно) и не отличались существенно между группами («восходящая»: среднее ω = 0.37 ± 0.06 SE; «нисходящая»: среднее ω = 0.47 ± 0.06 SE; тест Манна-Уитни U: U = 664, z = 1.77, p = 0.077, r = 0.19, 95% CI = (-0.03, 0.40)). Это указывает на то, что участников в обеих группах можно было условно разделить на тех, чья асимметрия обучения была или не была чувствительна к изменениям в силе предпочтения выбора, в соответствии с различием между адаптивными и неадаптивными участниками по Q_asymm2.

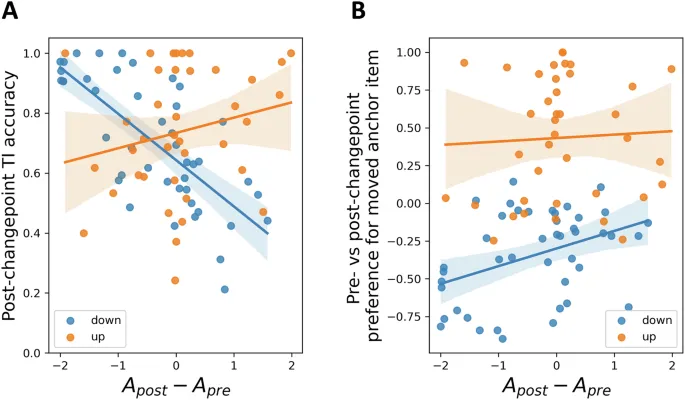
Интересно, что «нисходящие» участники, у которых это изменение в асимметрии обучения было наиболее выражено, как правило, были теми, кто демонстрировал относительно высокую производительность после точки изменения. Например, разница между α⁻_post и α⁺_pre у участников по Q_asymm2 была значительно отрицательно коррелирована с их точностью ТИ вне якоря после точки изменения и, следовательно, с их способностью реагировать на точку изменения, минимизируя при этом нарушение неизменной транзитивной иерархии (коэффициент ранговой корреляции Спирмена: r = -0.73, p < 0.001; рис. 6A). Аналогично, это снижение асимметрии обучения после точки изменения было положительно коррелировано с изменением предпочтения участников между фазами до и после точки изменения для перемещенного якоря i7, так что участники, которые правильно снизили свое предпочтение для i7, показали большее снижение своей предвзятости к победителям после точки изменения (r = 0.37, p = 0.015; рис. 6B). В отличие от этого, ни одна из этих значительных связей не наблюдалась у «восходящих» участников, ни в отношении их точности ТИ вне якоря после точки изменения (r = 0.21, p = 0.209), ни их изменения предпочтения для перемещенного якоря i1 (r = 0.11, p = 0.487). Эти результаты еще больше подтверждают идею о том, что, хотя точка изменения, испытанная «нисходящими» участниками, нарушала обучение ТИ на групповом уровне, хорошо работающие участники тем не менее могли использовать адаптивное снижение предвзятости к победителям, чтобы более адекватно реагировать на изменение истинной структуры.

Валидация модели

В качестве последнего шага валидации модели мы симулировали наши кандидатные модели, используя наилучшие эмпирические параметры, а затем проанализировали полученные вероятности выбора, чтобы проверить, какие модели способны качественно воспроизвести ключевые поведенческие эффекты, наблюдаемые в нашем эмпирическом наборе данных36,37. Сначала мы исследовали согласованность эффектов сжатия ценности, оцененных человеком и моделью. В соответствии с описательными результатами (см. рис. 3A, верхняя левая панель), производительность ТИ до точки изменения как Q_adapt, так и Q_asymm2 характеризовалась сжатой структурой ценности, причем наклоны асимметрии были значительно ниже 0 (Q_asymm2: «восходящая»: среднее β = -0.02 ± 0.005 SE, t(38) = -3.96, p < 0.001, d = -0.63, 95% CI = (-0.03, -0.01); «нисходящая»: среднее β = -0.02 ± 0.004 SE, t(43) = -4.54, p < 0.001, d = -0.68, 95% CI = (-0.03, -0.01); Q_adapt: «восходящая»: среднее β = -0.02 ± 0.01 SE, t(38) = -3.89, p < 0.001, d = 0.62, 95% CI = (-0.03, -0.01); «нисходящая»: среднее β = -0.01 ± 0.01 SE, t(43) = -2.44, p = 0.019, d = -0.37, 95% CI = (-0.03, 0.00)).

Затем мы определили участников как склонных к победителям или проигравшим в соответствии с их индексом асимметрии до точки изменения α⁺_pre (Q_asymm2) или знаком их наилучшего параметра α₀ (Q_adapt). Обе модели дали оценки доли участников, попавших в каждую категорию, которые были более близки к тем, что были получены из модели-агностической меры, т. е. знака наклона асимметрии до точки изменения у участников (количество участников, склонных к победителям, по Q_asymm2: «нисходящая»: 32/44 участника; «восходящая»: 28/39 участника; количество участников, склонных к победителям, по Q_adapt: «нисходящая»: 25/44 участника; «восходящая»: 33/39 участника; см. рис. 4B и рис. S2). Это контрастирует с Q_asymm, которая не смогла воспроизвести значительный отрицательный наклон асимметрии у «нисходящих» участников («восходящая»: среднее β = -0.02 ± 0.01 SE, t(38) = 4.03, p < 0.001, d = -0.64, 95% CI = (-0.03, -0.01); «нисходящая»: среднее β = -0.01 ± 0.01 SE, t(43) = -1.44, p = 0.157, d = 0.22, 95% CI = (-0.02, 0.00)), а также недооценила долю участников, склонных к победителям, согласно ее индексу асимметрии A на основе модели, как сообщалось ранее.

Переходя к поведению моделей в зависимости от точки изменения, мы повторили наш смешанный ANOVA 2 × 2 на точности выбора ТИ вне якоря наших моделей, с точкой изменения (до против после) в качестве внутрисубъектного фактора и направлением («восходящее» против «нисходящего») в качестве межсубъектного фактора. Интересно, что, несмотря на то, что обе модели оказались лучшими с точки зрения соответствия поведенческим данным, а также качественно воспроизводили изменения в точности ТИ, связанные с точкой изменения (рис. 2, крайние правые панели), Q_asymm2 не смогла воспроизвести значительный эффект взаимодействия точки изменения × направления, наблюдаемый у людей (F(1,81) = 2.56, p = 0.113, η_p² = 0.03, 95% CI = (0.00, 0.13); рис. 3B, правые панели), как и статическая асимметричная модель Q_asymm (F(1,81) = 3.60, p = 0.061, η_p² = 0.04, 95% CI = (0.00, 0.15); рис. S7B, центральные панели). В отличие от этого, производительность ТИ Q_adapt различно зависела от изменения лежащей в основе истинной структуры ранжирования, демонстрируя значительный эффект взаимодействия точки изменения × направления на точность ТИ вне якоря (F(1,81) = 4.17, p = 0.044, η_p² = 0.05, 95% CI = (0.00, 0.16)). Это было обусловлено значительным улучшением точности ТИ от до к после точки изменения для «восходящих» участников, моделируемых Q_adapt (до точки изменения: средняя точность = 0.67 ± 0.02 SE; после точки изменения: средняя точность = 0.75 ± 0.03 SE; t(38) = 6.56, p < 0.001, d = 1.05, 95% CI = (0.06, 0.11)), в отличие от гораздо менее выраженного, хотя и все еще значительного, увеличения точности ТИ между точками изменения для «нисходящих» участников, моделируемых Q_adapt (до точки изменения: средняя точность = 0.68 ± 0.02 SE; после точки изменения: средняя точность = 0.72 ± 0.02 SE; t(43) = 2.43, p = 0.039, d = 0.37, 95% CI = (0.01, 0.07)). То есть, точность ТИ вне якоря Q_adapt была относительно снижена в «нисходящей» группе после точки изменения, в то время как производительность продолжала улучшаться в «восходящей» группе (рис. S7B, правые панели).

Интересно, что точная картина нарушения ТИ у «нисходящих» участников отличалась от предсказанной Q_adapt; в то время как наши модели предсказывали более выраженное снижение в сравнениях с более низкой ценностью, пагубное влияние «нисходящей» точки изменения, как правило, сильнее отражалось в сравнениях с более высокой ценностью (рис. 2, нижние панели). Учитывая сходство в размерах эффекта для взаимодействий в наших двух выигрышных моделях Q_asymm2 и Q_adapt, мы далее искали более формальную оценку этого кажущегося расхождения в способности этих моделей воспроизводить ключевой эффект взаимодействия, представляющий интерес. Для этого мы включили «модель» в качестве дополнительного внутрисубъектного фактора в смешанный ANOVA, описанный выше. Это выявило незначительное взаимодействие модели × точки изменения × направления (F(1,81) = 0.22, p = 0.637, η_p² = 0.003, 95% CI = (0.00, 0.06)) – то есть, модели не отличались существенно друг от друга по степени, в которой они демонстрировали зависимый от направления эффект точки изменения на точность ТИ.

Таким образом, оценка не только свидетельства модели для каждой из наших кандидатных моделей (т. е. «предсказательной производительности»), но и их способности генерировать поведенческие паттерны, похожие на те, что наблюдались у людей (т. е. «генеративной производительности»37), показала несколько неоднозначную картину относительно превосходства Q_asymm2 по сравнению с Q_adapt – в то время как первая продемонстрировала явное преимущество с точки зрения AIC, последняя была незначительно лучше в воспроизведении основного интересующего поведенческого эффекта, хотя и не статистически значимо. В любом случае, это подтверждает аргумент о том, что ТИ человека лучше всего описывались RL-моделями, чья асимметрия обновления убеждений не остается статической на протяжении всего обучения.

Обсуждение

ТИ является примером впечатляющей способности людей и других животных использовать знания, полученные о локальных отношениях, для вывода глобальных, невидимых отношений. Вводя различные изменения в реляционную структуру, мы продемонстрировали, что предвзятое обновление убеждений обеспечивает различные уровни гибкости для адаптации к таким изменениям в истинной упорядоченности: в то время как перемещение худшего элемента «вверх» на вершину иерархии легко принимается, перемещение лучшего элемента «вниз» к основанию имеет более разрушительное воздействие на последующие инференционные знания.

Сжатие участниками их выученных структур ценности составляет пример более обобщенного искажения, широко наблюдаемого в психофизических, числовых и экономических контекстах принятия решений, где различимость между сравниваемыми объектами уменьшается с увеличением интенсивности или величины стимула42,43,44,45,46. Здесь мы предполагаем, что такие сжатые представления могут возникать из асимметричного правила обучения (см. также ссылку 5). Тем не менее, мы ни в коем случае не утверждаем, что предвзятости обновления убеждений являются единственным источником этих повсеместно наблюдаемых психометрических искажений. Мы отмечаем, что снижение различимости из-за увеличения общих оценок ценности по всей иерархии не противоречит точке зрения, что сжатые суждения о величине могут возникать, например, из ментальной организации числовой информации по степенной или логарифмической шкале44,45.

Действительно, мы наблюдали расхождение в том, как человеческая и симулированная производительность ТИ зависели от «нисходящей» точки изменения в зависимости от суммарной ценности пары, причем сравнения с более высокой ценностью, казалось, были наиболее сильно нарушены у людей, но в меньшей степени у наших симулированных асимметричных агентов. Это расхождение может указывать на наличие дополнительной сжимающей силы, которая еще больше снижает различимость сравнений с более высокой ценностью. Один из возможных способов различения относительных вкладов асимметричных политик и нелинейного «масштабирования Вебера» внутренних представлений в области реляционного обучения — это более тщательное изучение индивидуальных различий участников в знаке асимметричной предвзятости обучения: если эффекты поведенческого сжатия, проявляемые участниками, склонными к победителям, были эквивалентны эффектам антисжатия участников, склонных к проигравшим, с равными абсолютными асимметриями обучения, то это еще больше подчеркнуло бы роль асимметричных политик обучения в возникновении сжатия ценности. Связано с этим, наблюдение противоположного эффекта взаимодействия точки изменения × направления, наблюдаемого в нашем эксперименте, но среди преимущественно склонной к проигравшим популяции, т. е. нарушения инференционных знаний среди «восходящей» группы, а не «нисходящей», подтвердило бы идею о том, что именно знак асимметрии обучения отвечает за любые (не)эффективные эффекты адаптации к точке изменения. Учитывая ограниченное количество участников, склонных к проигравшим, в данном исследовании, мы оставляем этот вопрос для будущей работы с большими и более разнообразными выборками участников.

Наши поведенческие предсказания были получены из Q_asymm, RL-агента, который масштабировал свои обновления победителей и проигравших парных сравнений в соответствии с асимметричными скоростями обучения, которые остаются фиксированными на протяжении всего эксперимента. Хотя эта модель значительно превзошла свой симметричный аналог Q_symm, она тем не менее недооценила долю участников, склонных к победителям. Это породило возможность того, что хорошо работающие участники в «нисходящей» группе были способны как адаптироваться к изменению реляционной структуры, так и демонстрировать эффекты сжатия до точки изменения, согласующиеся с первоначальным обучением, склонным к победителям. Поэтому мы ввели две дополнительные модели с различной степенью модуляции их асимметрии обучения. Q_asymm2, модель, которая претерпевает однократный сброс скоростей обучения после точки изменения, убедительно продемонстрировала наилучшую предсказательную производительность, но не дает информации о том, как могут возникать такие изменения в асимметрии обучения, вызванные точкой изменения. В отличие от этого, Q_adapt модулирует свою асимметрию скорости обучения от испытания к испытанию в зависимости от силы своего предпочтения выбора. Как теоретические, так и эмпирические работы указали на существенную роль неопределенности в формировании того, как животные учатся на обратной связи о вознаграждении, направляя использование привычного или целенаправленного контроля у людей47, гибкое сочетание информации о вознаграждении у приматов48 и адаптацию скоростей обучения, вызванную изменчивостью, посредством метаобучения у грызунов49.

Действительно, недавние исследования ТИ предполагают, что неопределенность парных сравнений может служить для их маркировки таким образом, чтобы сделать их более лабильными для последующей структурной реорганизации18. В отличие от этого, модулируя свою асимметрию обучения в зависимости от предпочтения одного из двух сравниваемых элементов, Q_adapt предлагает возможный механизм того, как эта модуляция асимметрии может возникнуть, одновременно объединяя недавние выводы о том, что асимметричные и симметричные политики обучения соответственно лучше объясняют поведение человека в частично и полностью обратной связи в режимах ТИ и действительно оптимальны для них5.

Q_asymm2 продемонстрировал значительное улучшение соответствия модели по сравнению как со статичной моделью обучения Q_asymm, так и с адаптивной моделью Q_adapt. Мы предварительно отмечаем, что только Q_adapt количественно воспроизвела значительное зависимое от направления влияние точки изменения на последующую инференционную точность, хотя формальное сравнение между этими эффектами взаимодействия в рамках двух выигрышных моделей не выявило статистически значимых различий. В любом случае, наши результаты указывают на то, что люди могут адаптировать свои преимущественно склонные к победителям асимметрии обучения, что поднимает вопросы о том, как эта адаптивность формируется неопределенностью.

Одним из многообещающих направлений для будущих исследований является рассмотрение того, как различные формы неопределенности могут по-разному влиять на эту асимметрию обучения. Существующие модели адаптации к точке изменения, как правило, обладают способностью разделять «алеаторную» неопределенность, относящуюся к ожидаемой вариабельности исхода, и «эпистемическую» неопределенность, возникающую из неожиданных изменений в изменчивой среде вознаграждения12,13,14. Точки изменения заставляют эти модели увеличивать свои скорости обучения до тех пор, пока не разрешится период высокой эпистемической неопределенности. В то время как предыдущие работы обнаружили свидетельства асимметричного ТИ обучения в стохастических условиях обратной связи5, наша задача включала детерминированную обратную связь, что делало обратную связь, указывающую на точку изменения, относительно заметной. Поэтому остается интересным открытым вопросом, пересекаются ли асимметрии обновления убеждений человека, склонные к победителям, и их способность адаптивно их изменять, с их способностью различать объективные реляционные изменения (т. е. изменчивость) от шумной обратной связи выбора (т. е. стохастичность).

Несколько направлений исследований связали элементарные предвзятости обновления убеждений с исследованиями в клинических условиях. В то время как предвзятости позитивности могут служить адаптивным средством для повышения позитивного самочувствия50 или мотивации6, сходящиеся эмпирические и теоретические работы также указывали на более пессимистичные скорости обучения в ряде симптомов Большого Депрессивного Расстройства51,52,53. Наше открытие, что предвзятости обновления убеждений обеспечивают различные уровни гибкости для изменений в реляционной структуре, поднимает интересные вопросы о том, пересекаются ли такие различия в адаптивности также с клиническими популяциями. Было бы особенно интересно рассмотреть такие асимметрии в адаптивности к точке изменения, особенно во время реляционного обучения, в контексте поведения, связанного с риском или азартными играми, поскольку они предсказывают различия во влиянии различных исходов — например, изменение ранее малоэффективной ставки по сравнению с изменением ранее высокоэффективной ставки — на ожидания вознаграждения, относящиеся к неизмененным ставкам. Хотя наша парадигма содержала полностью детерминированную реляционную обратную связь и, следовательно, не включала никакого риска или дисперсии исхода как такового, данные свидетельствуют о том, что степень асимметрии обучения формирует связь между изменчивостью вознаграждения в среде и склонностью индивида к поиску или избеганию риска54,55,56. Поэтому было бы целесообразно рассмотреть роль предвзятостей обновления убеждений в сжатии ценности и эффектах адаптации к точке изменения при различных уровнях дисперсии вознаграждения (т. е. через вероятностную реляционную обратную связь) и как эта связь может регулироваться клинически значимыми симптомами или чертами.

Наши RL-агенты представляли собой описательные модели того, как предвзятые политики обучения приводят к искажениям субъективной ценности и различиям в поведенческой адаптивности. Хотя мы не делаем причинных или механистических заявлений о динамике реляционного обучения в мозге, исследования, сосредоточенные на нейромодуляторной активности в базальных ганглиях и стволе мозга, могут предложить правдоподобные объяснения того, как обновления могут асимметрично масштабироваться во время RL. Более конкретно, субпопуляции нейронов стриатума с различными возбудительными и тормозными свойствами (т. е. рецепторы D1 и D2 соответственно) могут обеспечить средство дифференциального вовлечения опосредованного дофамином обучения в зависимости от положительных или отрицательных ошибок прогнозирования57,58,59. Аналогично, эмпирические работы привлекли внимание к системам серотонина, действующим в поведенчески релевантных временных масштабах, в способности отслеживать и адаптироваться к изменениям изменчивости сред вознаграждения49,60. Поэтому было бы интересно рассмотреть, как такие нейронные объяснения выходят за рамки задач с бандитами и затрагивают структурные настройки обучения, которые более явно задействуют процессы обобщения и вывода. Кроме того, наше исследование различий в адаптивности к изменениям в лежащей в основе реляционной структуре связано с исследованиями, изучающими, как нейронные и искусственные системы реконфигурируют знания на репрезентативном уровне в ответ на новую информацию. Данные свидетельствуют о том, что связывание транзитивных иерархий отражается в соединении нейронных многообразий в фронтопариетальных областях и глубоких нейронных сетях alike18. Изучение того, как различия в реляционной адаптивности, наблюдаемые в данном исследовании, могут быть воспроизведены в нейронной сети, в свою очередь, может дать нейробиологические гипотезы о том, как геометрические представления могут быть (не)эффективно реорганизованы в ответ на изменения в структуре окружающей среды.

Ограничения

Поскольку нашим основным фокусом было то, как реляционные изменения влияют на структурные знания, мы стремились идентифицировать участников, которые в достаточной степени выучили транзитивную иерархию до наступления точки изменения. Это потребовало применения того же порога производительности, который использовался Ciranka et al.5, но сфокусированного на испытаниях до точки изменения. Это составило несколько консервативный подход, с относительно высокой долей исключенных участников (см. «Участники» в Методах). Хотя фокусировка наших анализов на участниках, которые уже приобрели адекватные инференционные знания, была необходима для изучения любых изменений в этих знаниях, вызванных точкой изменения, это поднимает вопрос о обобщаемости наших утверждений о том, как асимметрии обучения обеспечивают различные уровни адаптивности к реляционным изменениям. Тем не менее, мы отмечаем, что применение более либерального порога для включения (α = 0.1, вместо 0.01), что привело к N = 103 участникам («восходящая»: N = 53; «нисходящая»: N = 50), не изменило наших основных выводов. То есть, мы также наблюдали дифференцированное влияние точки изменения на последующую производительность ТИ, которое лучше всего описывалось Q_asymm2 (рис. S8 и рис. S9A, B).

Мы также признаем, что RL-модели, реализованные в данном исследовании, представляют собой лишь узкую подмножество способов, которыми мы можем понять инференционное обучение и когнитивные процессы, которые его поддерживают. Например, можно было бы альтернативно исследовать проблему точки изменения ТИ в рамках схемы байесовского вывода, как это широко делалось в контексте ТИ3,38,61, и действительно, структурного обучения в более общем смысле62,63,64. В рамках этого широкого класса фреймворков нашу сценарий точки изменения ТИ можно рассматривать как проблему разрешения неопределенности обратной связи: новое наблюдение, что i7 < i1, поначалу одинаково соответствует как изменению ранга i1, так и изменению ранга i7, означая, что агент должен отслеживать вероятность последующей обратной связи выбора при каждой из этих гипотез о новой лежащей в основе истинной структуре. В то время как наши модели поддерживают только точечную оценку ценности каждого элемента, алгоритмы выборки, которые поддерживают апостериорное распределение оценок элементов (например, ссылка 38), могут быть лучше приспособлены для изучения того, как неопределенность в отношении элементов, занимающих разные части пространства ценности, может эволюционировать со временем.

Существует множество исследований, изучающих роль эпизодических процессов, вероятно, реализуемых в гиппокампе, в обеспечении вывода и обобщения65,66. Более конкретно, ТИ может поддерживаться «механизмами вывода на основе извлечения», которые реактивируют и комбинируют разделенные паттернами представления конкретных отношений41,67, или через более «основанное на кодировании» привлечение выведенных отношений посредством перекрывающихся структурных представлений68,69. Действительно, мы отмечаем, что Ciranka et al.5 обнаружили, что включение дополнительного компонента памяти на уровне пар, который позволял эпизодическое извлечение пар, для которых была предоставлена обратная связь, улучшало соответствие модели, захватывая усиленное обучение для прямых сравнений соседних элементов. Поскольку настоящее исследование было сосредоточено на том, как реорганизация реляционных знаний пересекается с широко наблюдаемыми предвзятостями в обучении ценности, мы не включали в наши модели возможность того, что транзитивное обучение может также включать эпизодические процессы памяти (ср. ссылки 5,41). Поэтому выяснение того, как и каким образом такие эпизодические процессы влияют на кэширование ценностей элементов, будет многообещающим направлением для будущей работы.