Фермиевский метод оценки: как повысить точность личных суждений и избежать ошибок

Введение в проблему точности оценок

С момента анализа Гальтона многочисленные репликации выявили два ключевых феномена: (а) среднее значение независимых оценок многих людей обычно ближе к истине, чем большинство отдельных оценок, и (б) его абсолютная ошибка меньше, чем среднее значение абсолютных ошибок каждой из оценок. Это явление стало известно как "мудрость толпы".

Однако агрегация эффективна и внутри одного человека: среднее значение двух оценок от одного и того же человека tends to быть лучше, чем первоначальная оценка этого человека — явление, названное "мудростью внутренней толпы". В то время как эффект мудрости толпы хорошо established, возникли споры относительно мудрости внутренней толпы, specifically, её измерения, robustness и модераторов.

Диалектический бустреппинг: классический подход

Отправной точкой нашего исследования стало фундаментальное исследование Херцога и Хертвига. Они просили участников указать, в каком году произошли важные исторические события. Subsequently, участникам было предложено предположить, что их первая оценка была ошибочной, подумать о причинах, почему она могла быть неправильной, и в конечном итоге дать вторую — альтернативную — оценку.

Херцог и Хертвиг обнаружили, что среднее значение первой и второй оценки данного участника для данного события было, в среднем, ближе к истине, чем одна только первая оценка. Более того, их инструкция привела к средним значениям, более близким к истине, чем в контрольной condition, где участники должны были дать вторую оценку, не следуя какой-либо стратегии.

Вдохновленные философом Гегелем, Херцог и Хертвиг объединили свою стратегию пересмотра под названием "диалектический бустреппинг": процесс, посредством которого initial thesis провоцирует antithesis, вызывая необходимость в synthesis.

Цель 1: Сравнение гегелевского подхода с фермиевским методом

Вместо того чтобы просто тестировать стратегию "рассмотреть противоположное" против контрольного condition, как это сделали Херцог и Хертвиг, мы также сравнили её с представителем нового класса competitors, которые мы называем фермиевскими. Ядерный физик и нобелевский лауреат Энрико Ферми (1901–1954) известен своими приблизительными оценками "на задней стороне конверта".

Фермиевская стратегия предполагает разложение проблемы на несколько подзадач, решение подзадач separately и, в конечном итоге, интеграцию решений этих подзадач — набора subestimates — в окончательную оценку. Преимущество такой процедуры может заключаться в том, что завышение оценок в одних подзадачах и занижение в других может partially компенсировать друг друга.

Экспериментальная методология

Мы собрали данные от 292 участников платформы Prolific с определенными критериями отбора. В конечном итоге, после исключений, окончательная выборка составила 285 участников (154 женщины; медиана возраста = 40 лет, стандартное отклонение возраста = 12.5).

Эксперимент состоял из четырех частей: (1) первая оценка, (2) вторая оценка, (3) задача попарного сравнения и (4) заключительные вопросы. Участникам потребовалось в среднем 62 минуты, и они получили фиксированное вознаграждение в размере 9.20 фунтов стерлингов.

Стимулы и задачи

В первой части участники давали оценки по 50 пунктам (пять свойств для каждого из 10 видов: масса тела, масса мозга, продолжительность жизни, период gestation, время сна для арабской лошади, серого волка, равнинной зебры, рыжей лисы, азиатского слона, короткоклювого дельфина, бенгальского тигра, ангорской козы, шимпанзе, большой панды). Истинное значение для данного пункта определялось как среднее значение двух источников.

После предоставления оценки участников просили указать нижний и верхний пределы таким образом, чтобы в 90% случаев истинные значения попадали между этими пределами.

Результаты исследования

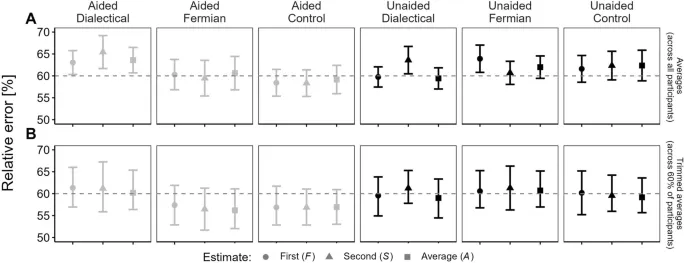
Мы оценили эффекты наших двух независимых переменных (стратегия и помощь памяти) с четырьмя зависимыми переменными и начинаем с этих результатов. Впоследствии мы исследуем over/underprecision и сравниваем эффект мудрости внутренней толпы с эффектом мудрости толпы.

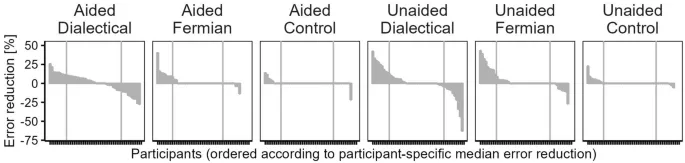
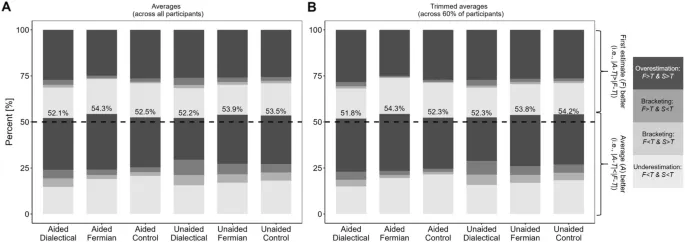
Предоставление второй оценки и последующее усреднение первой и второй оценок чаще приводило к улучшению по сравнению с рассмотрением только первой оценки: в каждом из шести conditions сумма четырех lowest categories превышала 50%.

Сравнение стратегий

Разница между этим числом и 50% может рассматриваться как одна из мер эффекта мудрости внутренней толпы. Преимущество фермиевской стратегии также проявилось, когда показатель D определялся после объединения условий с помощью памяти и без нее.

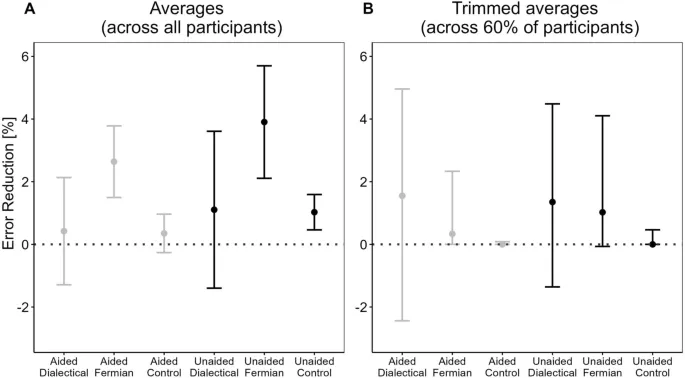
Среднее значение participant-specific median error reductions было наибольшим в двух фермиевских conditions (2.6% и 3.9%, а также significantly отличалось от нуля). Для прямых сравнений фермиевской стратегии с диалектическим бустреппингом (по всем conditions помощи памяти) мы вычислили p = 0.17, d = 0.2.

Влияние обработки данных на результаты

Когда центральная тенденция participant-specific median error reductions вычислялась с помощью усеченных средних, картина изменилась: теперь сокращение ошибок было наибольшим в двух диалектических conditions (1.55% и 1.35%). Для фермиевских conditions оно упало до 0.34% и 1.02%.

Сравнение результатов с усеченными и неусеченными средними показывает, что преимущество фермиевских стратегий в отношении сокращения ошибок исчезло при использовании усеченных средних. Это можно объяснить тем, что расчет усеченного среднего использует только 60% участников в середине данного распределения.

Точность и переоценка точности

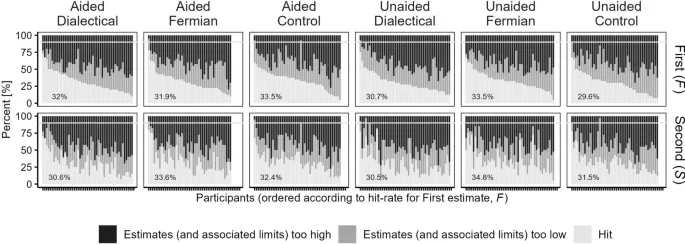
Мы определили over/underprecision как процент истинных значений, которые fell между пределами, указанными участниками. Учитывая, что участникам было предложено установить нижний и верхний пределы так, чтобы 90% истинных значений попадали между ними, hitrate в 90% указывал бы на точно выбранные доверительные интервалы, а hitrate ниже (выше) указывал бы на то, что диапазоны были слишком узкими (широкими).

Распределение hitrates участников revealed грубую overprecision (диапазоны слишком узкие), практически без разницы между conditions: вместо 90% средние значения hitrates участников (каждое вычисленное в данном condition) варьировались, across conditions, от 29.6 до 33.5% для первой оценки и от 30.5 до 34.8% для второй оценки.

Сравнение мудрости внутренней толпы и мудрости толпы

Мы сравнили beneficial effect генерации второй оценки с эффектом опроса другого человека. Specifically, для каждого пункта данного участника мы сравнили |A − T| с |AFi − T|, где AFi — среднее значение F этого участника и F другого участника (i), что привело к трем возможным исходам.

Как показано в результатах, в каждом из шести conditions участники чаще выигрывали, если бы они спрашивали другого участника об их первой оценке, чем если бы они спрашивали себя во второй раз (средняя разница = 8.3%, стандартная ошибка = 0.8%).

Обсуждение результатов

Преимущество опроса кого-то другого было наименьшим для двух фермиевских conditions, что согласуется с наблюдением, что фермиевские участники имели наибольшее сокращение ошибок (от F к S): те, кто получил наибольшую пользу от того, что спросили себя во второй раз, могли, по сравнению с другими conditions, получить меньше выгоды от опроса других.

Сильные и слабые стороны стратегий

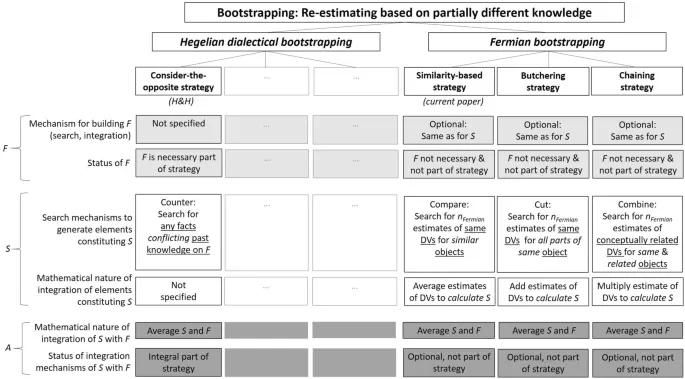
Гегелевский диалектический бустреппинг, реализованный с помощью инструкции "рассмотреть противоположное" Херцога и Хертвига, предписывает предполагать, что F неверен, искать причины, подтверждающие, что F ошибочен, и использовать эти причины для построения S. Эти принципы exhibit пять weaknesses.

Фермиевская оценка предписывает декомпозицию проблемы на nFermian ≥ 2 подзадач и агрегацию решений подзадач для генерации S. Фермиевские стратегии избегают weaknesses диалектической стратегии рассмотрения противоположного и имеют дополнительные strengths.

Практические implications

В соответствии с этим анализом, мы обнаружили: для большинства фермиевских участников медиана сокращения ошибок была равна нулю, а среди других фермиевских участников большинство benefited от генерации различных S (больше "победителей", чем "проигравших"). В среднем, сокращение ошибок было наибольшим в фермиевских conditions, тогда как для диалектических conditions оно практически не отличалось от контрольных conditions.

Однако эта картина результатов изменилась на противоположную при использовании participant-trimmed средних, которые barely изменили эффект для диалектического бустреппинга, но handicapped фермиевские conditions, eliminated, relatively speaking, больше "победителей", чем "проигравших" из меры размера эффекта.

Выводы и направления для будущих исследований

Важно отметить, что для фермиевских conditions S actually улучшилось по сравнению с F, тогда как для диалектических conditions S стало worse. Эффект мудрости внутренней толпы, Δ, был наибольшим в фермиевских conditions, и это несмотря на то, что helpful bracketing происходило чаще всего — и чаще всего способствовало Δ — в диалектических conditions.

Наконец, возможность извлечь выгоду из чужих F была наименьшей в фермиевских conditions. Будущие исследования могли бы также устранить ограничения текущего экспериментального design: фермиевская оценка требует, чтобы проблему можно было分解ить на nFermian ≥ 2 подзадач.

В конечном счете, только тогда, когда мы поймем, как характеристики диалектических, фермиевских и других "простых mental tools" взаимодействуют с task environment и с атрибутами пользователей инструментов, мы сможем grasp, насколько хорошо работают инструменты. До тех пор мы можем оставаться в недоумении относительно того, сколько мудрости действительно содержится в мудрости внутренних толп.