Моделирование восприятия времени: Обзор и применение к задаче временной генерализации

Введение: Важность отслеживания времени в поведении

Точное отслеживание хода времени имеет решающее значение для любого поведения. Возьмем, к примеру, игру с мячом: своевременность важна с разных точек зрения. С сенсорной точки зрения, нам необходимо постоянно отслеживать мяч и игроков, предсказывая их дальнейшие действия. С моторной точки зрения, мы должны точно рассчитать движения рук и ног, чтобы поймать мяч в нужный момент.

Нейробиологические и теоретические исследования показывают, что реализация отслеживания времени осуществляется различными способами, в зависимости от конкретной нейронной сети и поведенческой цели (Paton & Buonomano, 2018). Несмотря на это разнообразие, на алгоритмическом уровне поведенческие реакции, связанные со временем, часто описываются как процесс ограниченного накопления, известный в литературе по таймингу как «пейсмейкер-аккумуляторы» (pacemaker-accumulators) (Balcı & Simen, 2016; Simen et al., 2013).

К наиболее известным моделям этого семейства относятся модель Трейсмана (Treisman, 1963), теория скалярного ожидания (SET; Gibbon, 1977), поведенческая теория тайминга (BeT; Killeen & Fetterman, 1988) и модели дрейфа-диффузии для тайминга (driftdiffusion models of timing; Simen et al., 2011). В данной работе мы сосредоточимся на применении этих моделей к данным человеческого тайминга, а для более подробной информации отсылаем читателя к другим обширным обзорам (Balcı & Simen, 2024; Hass & Durstewitz, 2014).

Основные предположения моделей накопления времени

Центральным предположением моделей этого семейства является представление времени как результата накопления импульсов, генерируемых пейсмейкером. Простейшим примером таких моделей являются задачи, в которых участникам необходимо воспроизвести определенный временной интервал. Существует множество вариантов таких задач для человека, среди которых наиболее распространены продукция интервала (temporal production) и репродукция интервала (temporal reproduction).

• Продукция интервала: участникам предлагается воспроизвести одиночный интервал заданной длительности (например, 2,5 секунды; Kononowicz & Van Rijn, 2011; Macar et al., 1999).
• Репродукция интервала: участникам в каждом испытании предъявляется интервал переменной длительности, и их просят воспроизвести его (Cicchini et al., 2012).

Насколько нам известно, модели пейсмейкер-аккумуляторов формально не применялись к выполнению таких задач. Однако, аналогичная задача, к которой они применялись, — это задача «beat-the-clock» (Simen et al., 2011). В этой задаче участники должны отреагировать как можно ближе к установленному предельному сроку, но не позже него. Предельный срок меняется после непредсказуемого количества испытаний. Модель ограниченного накопления для «beat-the-clock» предполагает, что аккумулятор сбрасывается при начале отсчета интервала, и участник реагирует, когда накопленное значение достигает границы.

Моделирование принятия решений на основе временных интервалов

Модели ограниченного накопления широко применялись к задачам, связанным с принятием решений об истекших временных интервалах. К таким задачам относятся конструкции с вынужденным выбором одного интервала (1IFC — one-interval forced-choice) и двух интервалов (2IFC — two-interval forced-choice).

• 2IFC: В каждом испытании предъявляются два интервала, и участникам предлагается сравнить их (например, определить, какой интервал был длиннее; Kononowicz & Van Rijn, 2014).
• 1IFC: В каждом испытании предъявляется один интервал, и участникам предлагается сравнить его с длительностью (или длительностями), которым они научились в начале эксперимента. Прототипичным примером такой задачи является временное бисекция (temporal bisection), в которой участники классифицируют интервалы как «короткие» или «длинные» на основе двух эталонных интервалов, с которыми они ознакомлены в начале эксперимента (Allan & Gibbon, 1991; Church & Deluty, 1977; Wearden, 1991).

Согласно теории SET (Scalar Expectancy Theory), при бисекции участники сравнивают количество накопленных импульсов с сохраненными в памяти эталонами и реагируют в соответствии с тем, какой эталон наиболее близок к значению аккумулятора. Модель дрейфа-диффузии, адаптированная для временной бисекции, несколько сложнее, поскольку она была разработана для объяснения не только бинарных ответов «короткий»/«длинный», но и времени реакции (response times) (Balcı & Simen, 2014).

Эта модель предполагает, что аккумулятор работает до тех пор, пока не будет достигнута граница принятия решения, после чего интервал классифицируется как «длинный», или пока интервал не закончится. Если интервал заканчивается до того, как аккумулятор достигнет границы, запускается вторая модель дрейфа-диффузии, в которой накопленное значение сравнивается с внутренней точкой бисекции. Пренебрегая шумом, если накопленное значение больше точки бисекции, интервал классифицируется как «длинный». Если оно ниже точки бисекции, то интервал классифицируется как «короткий».

Концептуальное преимущество модели дрейфа-диффузии

Концептуальным преимуществом модели дрейфа-диффузии является то, что она естественным образом интегрирует восприятие времени в более широкую область принятия перцептивных решений (Ratcliff et al., 2016). Эта объединяющая перспектива особенно полезна для исследований, связывающих физиологию с поведением, поскольку она позволяет опираться на обширный объем литературы о нейронных основах принятия решений (O’Connell & Kelly, 2021).

Действительно, было обнаружено, что процессы принятия временных решений отражаются в признаках моторной подготовки и накопления доказательств (Ofir & Landau, 2022, 2025).

Расширение модели дрейфа-диффузии на задачу временной генерализации

Учитывая успешность модели дрейфа-диффузии в объяснении производительности и данных электроэнцефалографии (ЭЭГ) в различных временных поведений, мы задались вопросом, может ли она быть применена и к другим задачам принятия временных решений. Одним из таких примеров является задача временной генерализации (temporal generalization task), введенная в исследования человека Джоном Уирденом (John Wearden, 1992).

В этой задаче участникам предлагается решить, совпадает ли длительность предъявленного интервала с ранее предъявленным эталонным. Задача временной генерализации остается относительно малоизученной экспериментальной конструкцией. Мы полагаем, что одна из причин заключается в отсутствии простых в использовании установленных моделей. Это контрастирует с другими, более распространенными конструкциями, такими как временная бисекция или дискриминация, которые дают сигмоидальные данные, поддающиеся анализу с помощью широко доступных наборов инструментов для психофизических данных, таких как Psignifit (Schütt et al., 2016) и Palamedes (Prins & Kingdom, 2018).

Значение различных экспериментальных дизайнов

Каждый экспериментальный дизайн полезен, поскольку он подчеркивает различные части когнитивного процесса. Репродукция интервала акцентирует внимание на компонентах моторного тайминга, в то время как временная генерализация подчеркивает аспекты принятия перцептивных решений в поведении, связанном со временем. Описание производительности в области тайминга в различных задачах на когнитивном уровне необходимо для получения полной картины того, как животные вычисляют и используют время. Сложность тайминга на нейронном уровне подчеркивает важность изучения времени с использованием множества дизайнов, поскольку то, как осуществляется тайминг в одной задаче, не обобщается на другие задачи (Paton & Buonomano, 2018).

Методологические цели исследования

Наша работа преследует несколько методологических целей:

1. Суммирование и предоставление кода для моделей: Мы обобщаем три существующие модели временной генерализации, а также новую модель, и предоставляем код для их подгонки с использованием подхода максимального правдоподобия.
2. Сравнение моделей на уровне отдельных участников: Существующие модели никогда не тестировались и не сравнивались тщательно. Предыдущие работы с участием людей подгоняли модели только к данным, усредненным по всем участникам (Birngruber et al., 2014; DroitVolet et al., 2001). Из-за индивидуальной вариабельности групповые данные часто не отражают поведение на уровне отдельных участников (Ratcliff, 1979) и являются субоптимальными для тестирования моделей, предназначенных для применения к отдельным лицам. Чтобы восполнить этот пробел, мы сравниваем восстанавливаемость параметров различных моделей и их соответствие данным отдельных участников. Мы также рассматриваем восстанавливаемость моделей — насколько точно мы можем определить, какая модель из рассматриваемого набора породила набор данных.

Эмпирические исследования

На эмпирическом уровне мы проводим два эксперимента:

• Эксперимент 1: Сравнение модальностей: Первый эксперимент сравнивает временную генерализацию в визуальной и слуховой модальностях. Известно, что слуховой тайминг превосходит зрительный (Cicchini et al., 2012; Di Luca & Rhodes, 2016; EspinozaMonroy & De Lafuente, 2021; Wearden et al., 1998). Задача временной генерализации в сочетании с когнитивной моделью позволяет тестировать различия между модальностями на уровнях восприятия и принятия решений.
• Эксперимент 2: Влияние обучения: Второй эксперимент исследует влияние обучения на задачу. Гипотетически, обучение может проявляться как улучшение точности тайминга, так и как изменение аспектов принятия решений (Masís et al., 2023).

Помимо возможности сравнения моделей на эмпирических данных, эти эксперименты служат полезным инструментом для сравнения поведения в различных условиях.

Временная генерализация: Структура эксперимента

Описание задачи

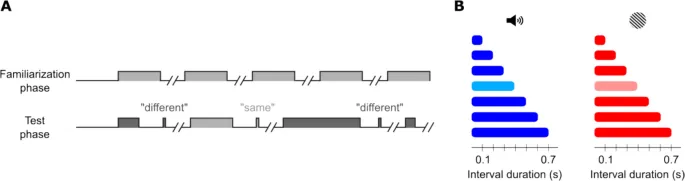
Прежде чем углубляться в модели, представим структуру эксперимента по временной генерализации. Типичный эксперимент по временной генерализации состоит из нескольких блоков испытаний с одинаковой структурой (Рис. 1A).

• Фаза ознакомления (familiarization phase): Каждый блок начинается с нескольких повторений эталонной длительности, на которые участникам не предлагается отвечать.
• Тестовая фаза (test phase): Затем начинается тестовая фаза. В каждом испытании этой фазы участнику предъявляется одиночный интервал, и его просят сообщить, имеет ли интервал такую же длительность, как эталонная, или нет. Предъявляемая длительность варьируется от испытания к испытанию и обычно охватывает диапазон, равномерно распределенный вокруг эталонного значения (Рис. 1B).

На протяжении всего текста мы будем использовать термин «то же» (same) для обозначения суждений участников об интервале как равном эталонному, в то время как «эталон» (standard) будет использоваться для описания фактической длительности интервала.

Визуальное представление эксперимента

Рис. 1. Схематическое представление задачи временной генерализации.

• A. Прогрессия фаз ознакомления и тестирования. В то время как фаза ознакомления пассивна, после каждого интервала в тестовой фазе участник должен ответить, прежде чем эксперимент продолжится.
• B. Графическое резюме эксперимента 1 — эксперимента по временной генерализации, разработанного для сравнения производительности в слуховой (синий) и зрительной (красный) модальностях. Этот дизайн включает семь тестовых длительностей (включая эталонную 0,4 с, показанную более светлыми цветами).

Моделирование производительности в задаче временной генерализации

Психометрическая кривая как показатель

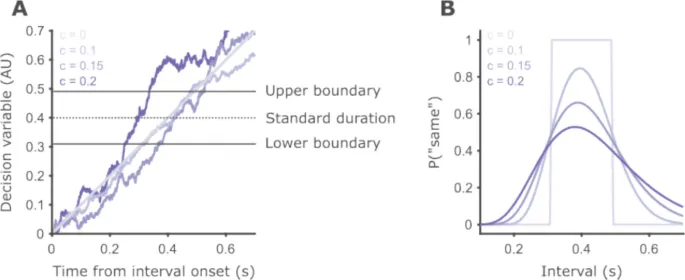
Производительность в задаче временной генерализации обычно суммируется путем построения психометрической кривой — вероятности ответов «то же» как функции длительности интервала (Рис. 2B). Эта функция также иногда называется градиентом генерализации (generalization gradient).

От коротких к длинным интервалам вероятность ответа «то же» плавно возрастает до максимума, который находится на эталонной длительности или близко к ней, а затем снижается для более длинных интервалов. Кривые обычно асимметричны относительно своего максимума: восходящая часть кривой (т. е. для интервалов короче эталонного) более крутая, чем нисходящая.

Это основные свойства, которые должны демонстрировать все модели временной генерализации. Помимо этого, подходы различаются тем, на какие аспекты они фокусируются — теоретические или методологические (Wilson & Collins, 2019).

• Подходы на основе SET: подчеркивают, что модели должны демонстрировать «масштабную инвариантность» (scale invariance) — умножение интервалов в задаче на коэффициент должно приводить к наложению психометрических кривых (Church & Gibbon, 1982).
• Наш подход: В данной работе мы делаем акцент на использовании моделей для суммирования поведения в когнитивно значимые параметры как инструмент для изучения поведения в различных условиях (Wichmann & Jäkel, 2018).

Эти два аспекта не являются взаимоисключающими, и мы не считаем, что они должны конкурировать за важность. Эффективные описания данного поведения требуют теоретического понимания этого поведения, а теории поведения также должны обеспечивать адекватное соответствие эмпирическим данным.

Модель дрейфа-диффузии для временной генерализации

Рис. 2. Схематическое представление модели дрейфа-диффузии для временной генерализации.

• A. Основные компоненты модели — границы принятия решений (decision boundaries), установленные на 0,31 и 0,49, и переменная принятия решений (decision variable). Примеры эволюции переменной принятия решений во времени. Более темные оттенки соответствуют траекториям, смоделированным с большими коэффициентами диффузии. Для гипотетического случая отсутствия шума переменная принятия решений растет линейно как функция времени с наклоном 1. Траектории становятся более зазубренными с увеличением коэффициента диффузии.
• B. Психометрические кривые для границ принятия решений и трех уровней коэффициента диффузии, показанных на A. При отсутствии шума кривая представляет собой две ступенчатые функции, положение которых определяется параметрами границы. Для заданных границ принятия решений и используемых интервалов эта модель даст 100% точных ответов. По мере роста внутреннего шума кривые становятся шире, с более пологими наклонами, и асимметрия увеличивается.

Все рассматриваемые модели основаны на общем подходе в моделях восприятия: на каждом испытании извлекается выборка переменной принятия решений (DV), и эта выборка сравнивается с двумя границами принятия решений для получения бинарного решения: «то же», если DV находится в пределах границ, и «другое» в противном случае.

Модели различаются по нескольким параметрам:

• Симметричность границ принятия решений относительно истинной эталонной длительности.
• Наличие вариабельности границ между испытаниями.
• Зависимость шума во внутреннем представлении текущего интервала от длительности интервала.

В данной работе мы фокусируемся на когнитивных моделях для временной генерализации. Аналитические подходы, не предполагающие конкретную когнитивную модель, были недавно рассмотрены в других работах (Bausenhart et al., 2018; см. также Piras & Coull, 2011).

Модель Church & Gibbon (CG model, 1982)

Рассел Черч и Джон Гиббон изначально разработали модель для описания производительности крыс в задаче временной генерализации (Church & Gibbon, 1982; далее CG). Модель предполагает, что в каждом испытании из памяти извлекается случайная выборка эталонной длительности, а также случайная выборка границы принятия решения. Затем вычисляется абсолютное значение нормализованной разницы между текущей длительностью (предполагается, что она воспринимается точно) и выборкой эталонной длительности. Эта нормализованная разница сравнивается с границей принятия решения. Если абсолютная нормализованная разница меньше границы, интервал классифицируется как «то же», а если больше — как «другое».

Правило принятия решения может быть формализовано следующим образом:

$$b < rac{|t-s|}{s} < b$$

где s (эталонная память) и b (граница принятия решения) являются нормально распределенными случайными переменными, а t равно длительности, предъявленной в текущем испытании.

Психофизическая функция — вероятность маркировки интервала t как «то же» — была выведена Черчем и Гиббоном как:

$$P( ext{same}|t;B, k, igma_B) = hi(z_2) - hi(z_1)$$

где hi — стандартная нормальная кумулятивная функция плотности, а S — истинная эталонная длительность. Модель имеет три свободных параметра:

• B (среднее значение границы, относительное к эталону).
• {igma }_{B} (стандартное отклонение границы).
• k (коэффициент Вебера, определяющий вариабельность выборок эталонной памяти).

Примечание: Формула в исходном тексте, кажется, содержит ошибку. Стандартное представление для модели CG и ее модификаций часто использует абсолютное значение нормализованной разницы. В приведенной здесь формуле использовано предположение о стандартной структуре, однако для полного соответствия оригинальной работе требуется уточнение.

Модифицированная модель Church & Gibbon (MCG model, 1992)

Более поздние работы, разработавшие аналог экспериментального дизайна для человека, обнаружили, что люди демонстрируют большую асимметрию в своих психофизических кривых по сравнению с крысами (Wearden, 1992; далее MCG — «модифицированная Church & Gibbon»). Уирден предложил модифицировать DV, заменив выборку эталонной памяти в знаменателе на объективную длительность текущего интервала (переменные те же, что и в оригинальной модели Черча и Гиббона):

$$b < rac{|t-s|}{t} < b$$

Психофизическая функция может быть найдена путем алгебраических операций (Приложение 1) как:

$$P( ext{same}|t;B, k, igma_B) = hi(z_2) - hi(z_1)$$

где z_i зависят от t, S, B, {igma }_{B} и k.

Свободные параметры те же, что и для модели CG. Нормализация DV по длительности интервала вместо эталона означает, что вариабельность DV уменьшается для более длительных интервалов. Это свойство необычно для моделей тайминга, которые обычно предполагают, что неопределенность оцененной длительности возрастает для более длительных интервалов (Hass & Durstewitz, 2016). На протяжении многих лет были разработаны различные варианты этой модели для соответствия различным сценариям, таким как изменения в производительности с возрастом (DroitVolet et al., 2001; Wearden, 2004). Мы фокусируемся на самой простой версии, так как она обеспечивает наиболее четкое сравнение с другими моделями.

Модель Birngruber, Schröter & Ulrich (BSU model, 2014)

Как модели CG, так и MCG предполагают, что участники размещают свои границы принятия решений симметрично относительно истинной эталонной длительности. Это предположение кажется слишком строгим по двум причинам:

• Во-первых, отдельные участники часто демонстрируют индивидуальные смещения (biases) как в тайминге, так и в других формах восприятия, что приводит к смещенным психометрическим кривым (Gibbon et al., 1984; Lebovich et al., 2019).
• Во-вторых, некоторые экспериментальные манипуляции могут создавать систематические сдвиги в психометрических кривых среди участников.

Третья модель, которую мы рассматриваем, была разработана для данных, представляющих такой сценарий. Бирнгрубер и коллеги обнаружили, что когда сравнительный интервал является «чужеродным» (oddball) в последовательности стимулов, он воспринимается как более длинный, чем его объективная длительность (Birngruber et al., 2014; далее BSU). В частности, пик психометрической функции, то есть интервал, который чаще всего классифицируется как равный эталонному, короче эталонного.

Чтобы модель могла учитывать такие смещения, авторы предложили следующую психофизическую функцию:

$$P( ext{same}|t; b_1, b_2, arepsilon, k) = hieft(rac{b_2 (t + arepsilon s)}{kt} ight) - hieft(rac{b_1 (t + arepsilon s)}{kt} ight)$$

где s и t — объективные эталонный и сравнительный интервалы соответственно, k — коэффициент Вебера, описывающий, насколько быстро растет шум с увеличением сравнительного интервала, b_1 и b_2 — нижняя и верхняя границы соответственно, а arepsilon — параметр смещения.

Мы делаем два технических замечания. Во-первых, поскольку s — это объективная эталонная длительность, его единственное влияние заключается в том, что границы выражаются относительно эталона, а не в абсолютных терминах. Это можно сделать независимо от процедуры подгонки, если это необходимо. Во-вторых, arepsilon полностью компенсируется границами. Для любого выбора arepsilon мы можем определить новые границы b_1' = b_1 arepsilon и b_2' = b_2 arepsilon , которые отменят эффект arepsilon. В оригинальной работе значение смещения ограничивалось дополнительными данными из отдельной задачи временной бисекции. Однако, когда доступны только данные из задачи временной генерализации, эта функция является перепараметризованной, и не все параметры могут быть оценены (см. также Приложение 2 в Birngruber et al., 2014).

Поэтому мы исключаем arepsilon и s из функции, получая упрощенную форму:

$$P( ext{same}|t; b_l, b_u, k) = hieft(rac{b_u t}{kt} ight) - hieft(rac{b_l t}{kt} ight)$$

Эта модель, по сути, утверждает, что зашумленная оценка сравнительного интервала сравнивается с двумя границами. Если она находится в пределах этих границ, она маркируется как «то же», и в противном случае — как «другое». Модель имеет три свободных параметра: верхнюю (b_u) и нижнюю (b_l) границы, и коэффициент Вебера k.

Предложенная модель дрейфа-диффузии (DDM)

Предыдущие исследования показали, что фреймворк дрейфа-диффузии хорошо описывает как поведенческие, так и различные аспекты нейронной активности в задаче временной бисекции (Balcı & Simen, 2014; Ofir & Landau, 2022). Мы предлагаем модифицированную модель дрейфа-диффузии (далее DDM), основанную на этом фреймворке, для задачи временной генерализации.

Предлагаемая модель включает один процесс дрейфа-диффузии с двумя границами. В отличие от типичной реализации DDM в сценариях с двумя выборами (Ratcliff et al., 2016), здесь обе границы устанавливаются выше начальной точки процесса дрейфа-диффузии. При начале интервала запускается процесс дрейфа-диффузии, и накопленное значение сравнивается с границами при завершении интервала.

• Если накопленное значение при завершении интервала не достигло нижней границы или превысило верхнюю границу, интервал классифицируется как «другое».
• В противном случае, если накопленное значение при завершении интервала находится между двумя границами, интервал классифицируется как «то же».

Психофизическая функция имеет вид:

$$p( ext{same}|t; b_l, b_u, c) = hieft(rac{b_u t}{cqrt t} ight) - hieft(rac{b_l t}{cqrt t} ight)$$

(см. Приложение 2 для математического вывода).

Модель имеет три свободных параметра:

• Коэффициент диффузии (diffusion-to-drift ratio, c): контролирует, насколько быстро растет шум со временем.
• Нижняя граница (b_l): отношение нижней границы к дрейфу.
• Верхняя граница (b_u): отношение верхней границы к дрейфу.

Для краткости параметры будут обозначаться как коэффициент диффузии и нижняя и верхняя границы. Отметим, что DDM и BSU очень похожи. Они различаются только тем, насколько быстро шум тайминга растет с длительностью интервала. Более быстрый рост вариабельности, предполагаемый BSU, приводит к кривым, которые, как правило, более асимметричны, чем те, что производятся DDM.

Сводка моделей

Подводя итог, все модели предполагают наличие переменной принятия решений (decision variable), которая сравнивается с границами принятия решений (decision boundaries).

Рассмотрим DDM в качестве примера. Мы визуализируем симуляции одиночного испытания с различными уровнями внутреннего шума, чтобы показать, как переменная принятия решений динамически эволюционирует (Рис. 2A). Мы также можем рассматривать модели через призму психометрических кривых, которые они производят (Рис. 2B).

Все четыре модели имеют параметры, контролирующие наклоны (восходящий и нисходящий) и асимметрию кривой, отражающие внутренний шум в процессе перцептивного принятия решений:

• DDM и BSU: ограничивают шум только процессом тайминга.
• CG и MCG: предполагают, что как тайминг (через память об эталоне), так и вариабельность решений влияют на наклоны.
• DDM и BSU: могут производить кривые, которые не центрированы относительно истинного эталона, в отличие от CG и MCG.

Методы симуляции

Данные и код для всех анализов доступны по адресу https://osf.io/87zbp/. Код для симуляционных анализов находится в файле “recovery_script.m”.

Подгонка моделей к поведению

Процедура подгонки

Три свободных параметра каждой модели оценивались с помощью численной процедуры максимального правдоподобия, аналогично подгонке других психофизических функций (Prins & Kingdom, 2018).

1. Сначала вычислялась вероятность ответа «то же» для каждой длительности при заданном наборе параметров.
2. Затем суммировались логарифмы вероятностей для всех испытаний одного участника в одном условии.
3. Набор параметров, достигший максимального правдоподобия, находился численно с помощью алгоритма Нелдера-Мида, реализованного в функции fminsearch MATLAB (MathWorks, MA).

При работе с подгонкой моделей CG и MCG мы заметили, что fminsearch иногда пытался использовать комбинации двух параметров наклона, которые приводили к мнимым числам в знаменателе психофизической функции, вызывая ошибки MATLAB. Поэтому, специально для MCG и CG, мы ограничили все параметры положительными значениями с помощью fmincon.

Инициализация поиска

Для всех моделей мы инициализировали численную оптимизацию из восьми стартовых точек в пространстве параметров (все комбинации двух значений для каждого из трех параметров). Значения описаны в Таблице 1. Эти значения были выбраны таким образом, чтобы процедура подгонки начиналась с нескольких типов кривых: от почти плоских до очень узких, а также смещенных по горизонтали (в случае DDM и BSU, которые допускают это). Эти значения также были выбраны, поскольку они дают конечные правдоподобия (Wilson & Collins, 2019). Для CG и MCG, поскольку модели работают с длительностями, нормализованными относительно эталона, мы использовали специфические числа. Границы принятия решений для BSU и DDM были выбраны на основе диапазона интервалов в эксперименте.

Таблица 1. Начальные предположения для различных параметров и моделей

[В этом месте должна быть таблица с начальными значениями параметров. Поскольку таблица отсутствует в исходном тексте, она не может быть воспроизведена.]

Восстановление параметров (Parameter Recovery)

Определение и важность

Важным шагом в тестировании модели является изучение ее способности подгонять данные, которые она сама симулировала. Это называется восстановлением параметров (parameter recovery) и измеряет способность модели к подгонке в идеальных условиях (Wilson & Collins, 2019). В анализе восстановления параметров набор данных симулируется моделью с заданными параметрами, а затем эта модель подгоняется к симулированным данным для оценки параметров модели.

Если параметры модели хорошо определены и сбор данных соответствует требованиям, мы ожидаем, что оцененные значения параметров будут близки к значениям, использованным для симуляции данных.

Подготовка данных для восстановления параметров

Чтобы гарантировать, что тестируемые значения параметров отражают значения, наблюдаемые в реальном поведении, мы подогнали вероятностные распределения к оцененным значениям параметров поведения участников в двух проведенных нами экспериментах (Рис. S1). Это было сделано для каждого параметра отдельно (всего 12 независимых распределений, по три для каждой из четырех моделей).

Каждый участник в каждом условии рассматривался как независимая точка данных. Для контроля влияния выбросов на восстановление параметров мы удалили точки данных, в которых любой из параметров находился более чем в трехкратном межквартильном диапазоне (IQR) от медианы. Всего было удалено от 8 до 35 точек данных для каждой модели, что привело к количеству точек данных от 150 до 177 на параметр для каждой модели.

Мы вручную выбрали распределения, чтобы разумно соответствовать значениям параметров, при этом симулируя только неотрицательные значения. Гамма-распределения были подогнаны ко всем параметрам моделей DDM и BSU, а также к параметру разделения границ моделей CG и MCG. Из-за большого количества параметров шума, близких к нулю, в CG и MCG (см. результаты экспериментов), мы использовали экспоненциальные распределения как для параметров вариабельности границ, так и для параметров вариабельности тайминга в этих моделях.

Проведение симуляций

Для каждой модели было сгенерировано 5000 симуляций из распределений параметров, используя то же количество испытаний, что и в одном из условий эксперимента 1 (см. Экспериментальные методы). Симулированные параметры были независимыми, за исключением нескольких случаев, которые могли вызвать проблемы при последующей подгонке симулированных данных.

• DDM и BSU: Верхние границы должны быть достаточно больше нижних, иначе модель маркирует все интервалы как «другое». Чтобы предотвратить такие случаи, мы перегенерировали параметры, у которых верхняя граница была меньше нижней границы более чем на 0,1.

Наконец, результаты каждой симуляции были подогнаны той моделью, которая ее создала, и оцененные и симулированные параметры были сравнены.

Обработка результатов симуляции

Часть симуляций привела к подгонкам с очень большими оцененными значениями параметров, далекими от групповых. Поэтому мы удалили все симуляции, в которых оцененное значение параметра было больше, чем в пять раз больше максимального симулированного значения. Это привело к удалению менее 3,5% симуляций для каждой модели.

В качестве общей меры точности подгонки мы рассчитали коэффициент корреляции Пирсона между симулированными и оцененными значениями параметров. Взаимосвязь параметров оценивалась с использованием корреляции между всеми парами оцененных значений параметров.

Восстановление моделей (Model Recovery)

Определение и цель

Восстановление параметров помогает понять, насколько надежно мы можем оценивать параметры модели из данных. Другой важный вопрос — насколько хорошо мы можем определить, какая из четырех моделей породила данные. Это особенно важно при сравнении моделей по их способности подгонять данные. Этот анализ называется восстановлением моделей (model recovery).

Процедура восстановления моделей

Чтобы оценить восстановление моделей в нашей установке, для каждой модели мы симулировали 1250 наборов данных, используя те же распределения параметров, что и в анализе восстановления параметров, что привело к общему количеству 5000 симулированных наборов данных.

Затем мы подогнали каждую симуляцию с использованием каждой из четырех моделей. Наконец, мы подсчитали количество симуляций, которые были лучше всего подогнаны каждой моделью, чтобы вычислить матрицу путаницы (confusion matrix).

Результаты симуляций

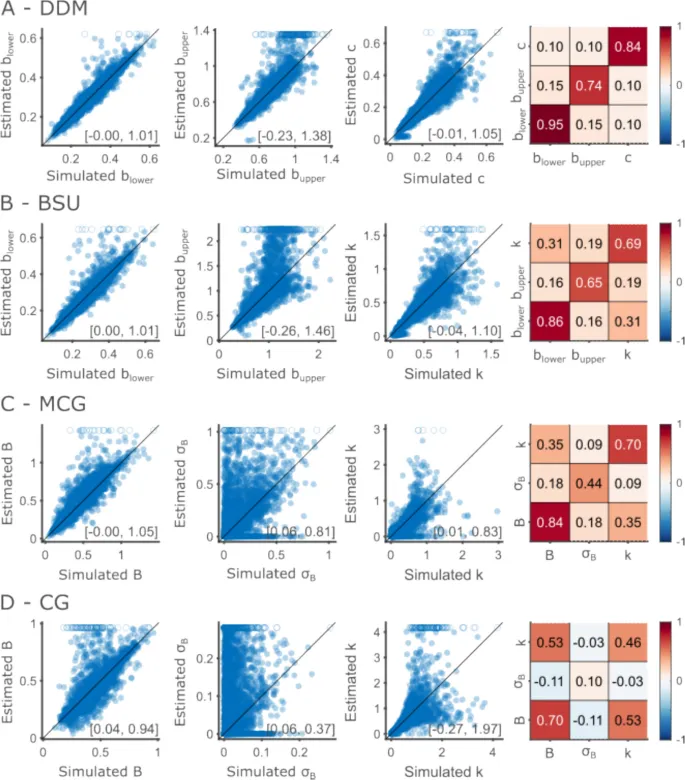
Параметры DDM восстанавливаются успешнее других моделей

Хорошие вычислительные модели должны быть идентифицируемыми: данный набор данных должен соответствовать уникальному набору значений параметров. Это можно проверить, анализируя восстановление параметров, или точность подогнанных параметров как оценок значений, породивших данные (Wilson & Collins, 2019). Мы использовали значения параметров, которые оценили на эмпирических данных, для генерации синтетических участников, для которых мы знали истинные значения.

Восстановление параметров DDM

Мы обнаружили, что модель DDM демонстрирует наивысшую общую точность восстановления для всех трех параметров (Рис. 3A). Верхние границы в целом оценивались хорошо, вплоть до значений около 0,8 секунды. Выше этой точки процедура подгонки имела тенденцию завышать оцененные верхние границы. Это означает, что оценки верхних границ, превышающие 0,8 с, следует рассматривать с осторожностью. Экспериментальный дизайн объясняет это наблюдение: самый длинный интервал, который мы тестировали, составляет 0,7 с, что означает, что верхние границы, превышающие эту точку, трудно оценить.

Межпараметрические корреляции были в целом низкими, оценивались на уровне 0,1 для корреляции между шумом и нижними и верхними границами, что указывает на хорошую идентифицируемость параметров. Коэффициент корреляции между верхними и нижними границами оценивался как 0,15. Симулированные границы были ограничены так, чтобы их разделение составляло не менее 100 мс, что привело к корреляции 0,11 между нижними и верхними симулированными границами. Часть наблюдаемой корреляции в оцененных значениях, вероятно, обусловлена корреляцией в симулированных значениях.

Восстановление параметров BSU

Параметры модели BSU восстанавливались несколько менее успешно (Рис. 3B). Это наиболее очевидно при оценке верхних границ в этой модели. Вариабельность оцененных верхних границ довольно быстро увеличивалась с увеличением симулированных верхних границ. Это приводит к более низкой восстанавливаемости, измеряемой корреляцией между симулированными и оцененными верхними границами. Отметим, что диапазон верхних границ, оцененных в наших данных, больше для BSU, чем для DDM. Это приводит к тому, что больше верхних границ симулируется выше 1, значения, которые трудно оценить, учитывая используемые нами интервалы.

Восстановление параметров MCG и CG

Параметры моделей MCG и CG восстанавливались наименее успешно (Рис. 3C, D). Разделение средней границы восстанавливалось относительно хорошо. Однако оба параметра шума — вариабельность границ и вариабельность тайминга — не были точно оценены. Вариабельность границ была особенно трудна для оценки, что наиболее ярко проявляется в модели CG, где оцененные значения разбросаны далеко от диагонали. Вариабельность тайминга восстанавливалась более точно.

Резюме восстановления параметров

Таким образом, параметры DDM восстанавливались хорошо в диапазоне параметров, которые мы оценили на эмпирических данных. Параметры BSU восстанавливались почти так же хорошо. Параметры шума CG и MCG в целом не восстанавливались точно, отражая компромисс между ними. Учитывая количество испытаний, имеющихся у нас в одном модальности, невозможно точно определить, обусловлена ли вариабельность производительности вариабельностью границ или вариабельностью тайминга.

Восстановление моделей: BSU лидирует

Все четыре модели восстанавливаются, при этом BSU является лидером.

После демонстрации восстанавливаемости параметров моделей и выявления недостатков, когда они были обнаружены, мы проверили, насколько возможно определить, какая из четырех моделей породила данные. Мы симулировали ответы 1250 синтетических участников для каждой модели, используя то же количество испытаний, что и в эксперименте 1. Затем мы подогнали все четыре модели к каждой из полученных 5000 симуляций и подсчитали количество симуляций, которые каждая модель подогнала лучше всего.

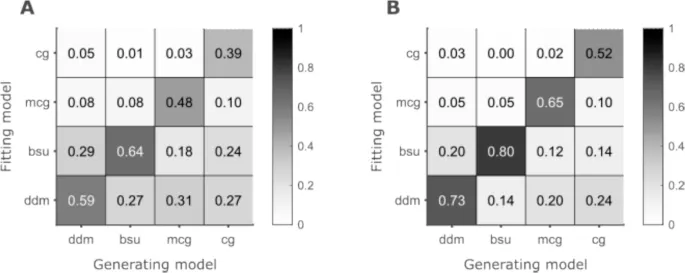
Общее количество испытаний в 225, как у нас в одном модальности, дало процент попаданий (hit rates) 39% для CG, 48% для MCG, 59% для DDM и 64% для BSU (Рис. 4). DDM и BSU, которые различаются только тем, как масштабируется шум тайминга, путались в 27–29% симуляций.

Увеличение количества испытаний в 3 раза до 675 испытаний улучшило восстанавливаемость всех моделей, как и ожидалось. Порядок моделей по проценту попаданий остался прежним: 52% для CG, 65% для MCG, 73% для DDM и 80% для BSU.

Рис. 4. Восстановление моделей.

• A. Восстанавливаемость при 225 испытаниях, как в эксперименте 1. Каждый столбец показывает результат одной порождающей модели и, следовательно, суммируется до 1. Каждая строка соответствует одной подгоняющей модели.
• B. То же, что и A, но для большого эксперимента с 675 испытаниями на участника.

Таким образом, мы обнаружили, что параметры DDM и BSU восстанавливались хорошо, в то время как параметр вариабельности границ моделей MCG и CG было особенно трудно восстановить точно. Восстановление моделей также было приемлемым для BSU и DDM при использовании 225 испытаний на участника. Относительно низкая восстанавливаемость MCG и CG отражается в тенденции DDM и BSU подгонять данные, которые они не породили. Это еще один результат низкой идентифицируемости параметра вариабельности границ MCG и CG. Несмотря на одинаковое количество параметров, DDM и BSU обладают большей функциональной гибкостью, чем MCG и CG. Теперь перейдем к описанию двух экспериментов, которые мы провели для проверки моделей на эмпирических данных.

Экспериментальные методы

Данные и код

Данные и код для обоих экспериментов, а также все анализы, доступны по адресу https://osf.io/87zbp/. Файл “modality_script.m” содержит анализ эксперимента 1, а файл “block_script.m” — анализ эксперимента 2. Файл “optimality_script.m” содержит код для анализа оптимальности.

Участники

Всего в двух экспериментах приняли участие 85 человек. Сорок участвовали в эксперименте 1 (32 женщины, средний возраст = 23,9, стандартное отклонение [SD] = 3) и 45 — в эксперименте 2 (32 женщины, средний возраст = 23,6, SD = 2,6). Шесть участников из каждого эксперимента были исключены из анализа (15% и 13,3% соответственно), так как они показали плоские психометрические кривые, что означает, что они не реагировали на предъявляемые интервалы (Рис. S2 и S3).

Экспериментальная процедура

Мы сообщаем о результатах двух поведенческих экспериментов, оба из которых проводились с использованием OpenSesame (Mathôt et al., 2012). Первый сравнивал временную генерализацию с визуальными и слуховыми стимулами, а второй — эффект обучения в задаче.

Оба эксперимента использовали 400 мс как эталонную длительность и семь уровней длительности стимула в качестве сравнительных стимулов (100, 200, 300, 400, 500, 700 и 800 мс).

Эксперимент 1: Сравнение модальностей

• Участники прошли две части: одна с визуальными стимулами, другая со слуховыми. Порядок частей был контрбалансирован между участниками.
• Каждая часть включала три блока по 75 испытаний каждый, разделенных перерывами.
• Эталонная длительность предъявлялась пять раз в начале каждого блока.
• В общей сложности все длительности, кроме эталонной, предъявлялись 30 раз, а эталонная — 45 раз в каждом модальности. Иными словами, эталон появлялся в 20% испытаний.
• Белая точка фиксации появлялась в центре экрана, когда на экране не было предъявлено никаких стимулов.

Эксперимент 2: Влияние обучения

• Мы использовали визуальные стимулы с двумя уровнями контрастности (50% или 100%).
• Эксперимент содержал шесть блоков по 80 испытаний каждый, разделенных перерывами.
• В дополнение к испытаниям, эталонная длительность предъявлялась шесть раз в начале каждого блока (по три в каждом контрасте).
• В конце блока на экране отображался процент точных ответов.
• Все длительности, кроме эталонной, предъявлялись 60 раз (30 в каждом контрасте, или 20 в каждом блоке), а эталонная — 120 раз (60 в каждом контрасте, или 40 в каждом блоке). Иными словами, эталон появлялся в 25% всех испытаний.
• Каждый блок содержал одинаковое количество испытаний для каждой длительности, представленных в разном порядке, чтобы облегчить изучение эффектов обучения.
• Белая точка фиксации появлялась в центре экрана, когда на экране не было предъявлено никаких стимулов.

Обратная связь и время реакции

В обоих экспериментах участники могли отвечать только после завершения предъявления стимула. В предыдущих экспериментах обратная связь предоставлялась после каждого испытания (например, Wearden, 1992). Мы предоставляли обратную связь в конце каждого блока испытаний, отображая на экране процент точных ответов за этот блок.

Эксперименты не были оптимизированы для сбора времени реакции, что требует дополнительной осторожности при использовании слуховых стимулов. В результате мы собрали действительные времена реакции только для эксперимента 2 и визуальной части эксперимента 1.

Стимулы эксперимента 1

• Визуальные стимулы: Квадратная решетка, предъявляемая в круговом окне на мониторе BenQ XL2420Z с частотой 144 Гц, расположенном на расстоянии 50 см от участников. Решетка имела пространственную частоту 1 цикл/см и диаметр 7 см (соответствующий 8° визуального угла) и располагалась в центре экрана. Решетки предъявлялись со случайной ориентацией 45° или 135°.
• Слуховые стимулы: Тона частотой 500 Гц, предъявляемые на комфортном уровне громкости через наушники Sennheiser HD 280 Pro.

Стимулы эксперимента 2

Эксперимент 2 был сосредоточен на визуальной модальности. Стимулы представляли собой те же квадратные решетки, что и в визуальной части эксперимента 1, предъявляемые с двумя уровнями контрастности. Оба уровня контрастности использовались для эталонных и тестовых стимулов и варьировались случайным образом между испытаниями.

Предыдущие исследования сообщают, что стимулы с более высоким контрастом воспринимаются как более длинные, чем аналоги с более низким контрастом (Matthews et al., 2011). Следовательно, мы предположили, что стимулы с более высоким контрастом будут смещать психометрическую кривую в сторону более коротких интервалов.

Анализ оптимальности

Мы дополняем наше сравнение различных моделей на эмпирических данных анализом оптимального поведения для DDM. Мы определили сетку из 2000 уровней шума в диапазоне, который мы эмпирически нашли, исключая выбросы, как определено в анализе восстановления параметров. Для каждого уровня шума мы искали границы принятия решений, которые максимизировали бы вероятность правильного ответа, или точность, при той же самой распределении интервалов, что и в эксперименте 1.

Мы искали максимизирующие точность границы численно с помощью алгоритма Нелдера-Мида, реализованного в функции fminsearch() MATLAB. Как объяснено в разделе результатов, мы повторили этот анализ дважды, с двумя распределениями длительностей. Во-первых, мы использовали структуру испытаний, как в реальном эксперименте, где 20% испытаний содержали эталонную длительность, а 13,33% — каждую из других шести длительностей. Во-вторых, мы провели анализ с 50% испытаний, содержащих эталонную длительность, и 8,33% для каждой из других длительностей. Кривые, описывающие оптимальные границы при различных уровнях шума, затем сравнивались качественно с фактическими комбинациями параметров, найденными в нашей выборке.

Статистический анализ

Общая точность анализировалась с помощью парных t-тестов, реализованных в функции ttest() MATLAB. Вероятность ответа «то же» как функция длительности интервала и других экспериментальных манипуляций анализировалась с использованием дисперсионного анализа (ANOVA) для повторных измерений в JASP (версия 0.19; JASP Team, 2024). Мы применяли коррекцию Гринхауса-Гейссера, когда тест Моучли указывал на нарушение предположения о сферичности.

Мы анализировали влияние экспериментальной манипуляции на когнитивные параметры, используя два подхода:

1. Подгонка отдельных моделей: Для обоих экспериментов мы следовали общему подходу, подгоняя одну модель к данным каждого участника в каждом условии отдельно, а затем сравнивая параметры с помощью t-тестов или ANOVA.
2. Сравнение моделей (эксперимент 2): Для эксперимента 2 мы дополнили этот анализ подходом сравнения моделей. Набор ограниченных моделей был подогнан к данным в дополнение к полной модели. В каждом ограниченном режиме мы сохраняли один из трех параметров фиксированным для всех условий, в то время как остальные могли свободно варьироваться для каждого условия. Это привело к трем ограниченным моделям: с фиксированными нижними границами, фиксированными верхними границами или фиксированными коэффициентами диффузии. Модели сравнивались на групповом уровне. Мы вычислили информационные критерии Акаике (AIC) для каждой модели на суммарных логарифмах правдоподобия и количестве свободных параметров по всем участникам.

Корреляции между параметрами и экспериментальными условиями тестировались с использованием линейных смешанных моделей, реализованных в функции fitlme() MATLAB.

Мы использовали бутстреп-подход на симуляциях из анализа восстановления параметров для создания нулевого распределения корреляции между верхней границей и шумом. В каждой из 5000 итераций мы случайным образом выбирали синтетических участников в том же количестве, что и в исходном эксперименте (33 и 36 для экспериментов 1 и 2 соответственно) и вычисляли коэффициент корреляции Пирсона. Наблюдаемое значение в эмпирических данных затем сравнивалось с этим распределением для вычисления бутстреп p-значения.

Результаты экспериментов

DDM лучше подгоняет данные отдельных участников, чем другие модели

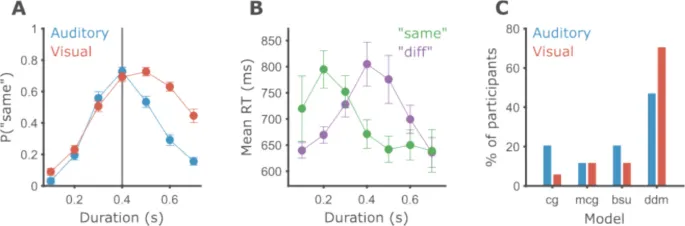
Мы проанализировали данные 34 участников, которые прошли две версии задачи временной генерализации: один блок с использованием слуховых чистых тонов и один — с визуальными решетками. В целом, участники лучше справлялись со слуховыми стимулами (Рис. 5A).

Участники показали значительно более высокую точность в слуховой модальности (M = 71,01%, SD = 9,52%), чем в визуальной (M = 58,77%, SD = 8,88%). Все участники, кроме одного, имели более высокую точность в слуховой модальности (парный t-тест, t(33) = 11,18, p < 0,001, d = 1,92).

Рис. 5. Участники лучше работают со слуховыми интервалами.

• A. Круги показывают среднюю вероятность маркировки интервала как «то же» по всем участникам, а полосы ошибок — внутриучастниковую стандартную ошибку среднего (SEM) с использованием метода Морея-Кусино (Cousineau et al., 2021). Вертикальная серая линия соответствует эталонной длительности. Синий цвет обозначает данные слуховой модальности, красный — визуальной.
• B. Среднее время реакции для ответов «то же» (зеленый) и «другое» (пурпурный) в зависимости от длительности интервала. Данные только для визуальной модальности.
• C. Процент участников (из 34) для которых каждая модель (на оси X) достигла наибольшего правдоподобия. Синий — слуховая модальность, красный — визуальная.

Мы провели ANOVA с повторными измерениями по вероятности ответов «то же» с длительностью интервала (семь уровней, 0,1–0,7 с), модальностью (два уровня: аудитория или зрение) и их взаимодействием как внутриучастковыми факторами. Мы обнаружили ожидаемый значительный основной эффект длительности интервала, F(6, 33) = 92,23, p < 0,001, {ta }_{p}^{2} = 0,74, указывающий на то, что участники обращали внимание на задачу. Кроме того, мы обнаружили значительный основной эффект модальности, F(1, 33) = 77,32, p < 0,001, {ta }_{p}^{2} = 0,7, а также значительное взаимодействие длительности и модальности, F(6, 33) = 17,23, p < 0,001, {ta }_{p}^{2} = 0,34.

Анализ времени реакции

Прежде чем подробно изучить различия между модальностями, кратко опишем паттерн времени реакции (RT) в задаче. Поскольку эксперименты не были оптимизированы для сбора RT, мы опишем только результаты визуальной части (Рис. 5B). Как и ожидалось, паттерны RT различаются в зависимости от принятого решения.

• Ответы «другое» были самыми быстрыми для самых коротких и самых длинных интервалов и самыми медленными вблизи эталонной длительности.
• Ответы «то же» были самыми медленными для коротких интервалов и выравнивались на более быстром RT около эталонной длительности.

Визуальное сравнение психометрических кривых

Визуальный осмотр бинарной производительности участников показывает, что психометрические кривые для слуховых и визуальных стимулов сильно различаются по форме. Различие между модальностями наиболее выражено для более длинных интервалов. Учитывая закон Вебера, это интуитивно соответствует большему коэффициенту вариации в зрении по сравнению со слухом: шум тайминга для статических решеток растет быстрее, чем для чистых тонов. Модели, описанные в первой части нашей работы, предоставляют формальные и статистические методы для проверки таких интуитивных предположений, как будет исследовано ниже.

Сравнение моделей на уровне отдельных участников

Сравнение производительности в различных условиях часто проводится путем суммирования производительности в каждом условии в параметры модели, а затем сравнения значений параметров между условиями. Для этого нам нужно установить, подходят ли модели, как по их способности подгонять данные, так и по степени определенности параметров модели.

Во-первых, мы сравнили способность четырех различных моделей подгонять данные на уровне отдельных участников. Для каждого участника мы подогнали каждую модель к данным каждого условия отдельно. Поскольку все модели имеют три свободных параметра, их можно напрямую сравнить по максимальному правдоподобию. Для обеих модальностей DDM значительно превзошла все другие модели (Рис. 5C), при этом 47,1% и 73,5% участников в слуховой и визуальной модальностях соответственно, по сравнению с вероятностью случайного угадывания 25% (Таблица 2). Явных систематических различий между тремя другими моделями не наблюдалось. Модели BSU и CG показали несколько лучшие результаты на слуховых, чем на визуальных данных. MCG показала одинаковые результаты в обеих модальностях.

Следуя предыдущим исследованиям, мы также подогнали модели к объединенным данным всех участников. В слуховой модальности лучшую производительность показала оригинальная модель CG, а в визуальной — модель MCG. В обеих модальностях DDM заняла второе место.

Таблица 2. Сравнение правдоподобия моделей в обеих модальностях.

В каждой модальности самый левый столбец включает процент и количество участников, для которых каждая модель лучше всего подогнала их данные. Средний столбец включает суммарный логарифм правдоподобия по всем участникам как меру общего соответствия модели. Правый столбец включает отношение правдоподобия DDM к правдоподобию каждой модели, суммированное по участникам в логарифмических единицах (log10). Поскольку количество свободных параметров одинаково для всех моделей, отношение правдоподобия равно отношению весов Акаике (Wagenmakers & Farrell, 2004). Учитывая очень большие различия в правдоподобии, меры весов доказательств, такие как веса Акаике, дали бы вес почти 1 DDM и почти 0 остальным трем моделям.

Важность подгонки к отдельным участникам

Как указано во введении, предыдущие работы с участием людей подгоняли модели только к объединенным данным на групповом уровне, что не обязательно отражает поведение отдельных участников. Действительно, мы обнаружили, что, несмотря на ограничение возможностью описать поведение отдельных участников, модель CG показала наилучшее соответствие групповым данным в слуховой модальности, а MCG — в визуальной. Этот результат демонстрирует, что подгонка к отдельным участникам имеет решающее значение при сравнении моделей.

Проблема идентифицируемости параметров в моделях CG и MCG

Обе модели, CG и MCG, имеют два параметра, контролирующих наклоны и асимметрию кривых: вариабельность границ и вариабельность памяти, контролируемую коэффициентом Вебера. Наличие более чем одного параметра, влияющего на психометрическую кривую схожим образом, может привести к проблемам с идентифицируемостью, когда изменения одного параметра могут быть компенсированы изменениями другого параметра (Gershman, 2016; van Maanen & Miletić, 2021).

Это означает, что оба параметра не могут быть надежно оценены одновременно на основе типичных эмпирических данных. Идентифицируемость особенно важна, если параметры используются для выводов, таких как сравнение между экспериментальными условиями. Чтобы проверить идентифицируемость параметров, мы исследовали оцененные значения параметров для всех моделей (Рис. 6).

Подгонки обеих моделей CG и MCG показывают тенденцию к уменьшению одного из двух параметров к нулю, чаще всего вариабельности границ, оставляя другому параметру объяснять всю объясненную вариабельность (Таблица 3). Это предполагает, что параметры наклона не являются идентифицируемыми.

Отметим, что это уже было кратко отмечено Уирденом (1992). Модель CG использовалась только для подгонки объединенных данных нескольких животных, каждое из которых выполнило сотни испытаний. Эти большие объемы данных, нетипичные для человеческой психофизики, возможно, позволили процедуре подгонки различить оба источника вариабельности (Gibbon et al., 1984). Однако для обсуждаемого нами типа данных эти модели являются субоптимальными.

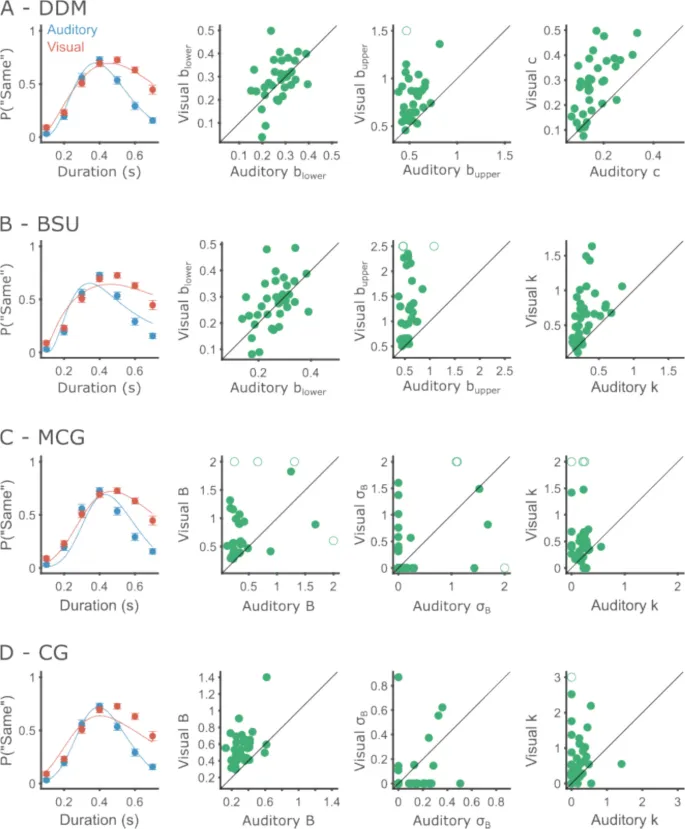
Рис. 6. Поведенческая производительность и подгонка моделей для Эксперимента 1.

• Каждый ряд показывает результаты одной модели.
• A. DDM. Слева — групповая производительность и подгонка модели. Круги показывают среднюю вероятность маркировки интервала как «то же» по всем участникам, а полосы ошибок — внутриучастниковую стандартную ошибку среднего (SEM). На диаграммах рассеяния показаны оцененные значения каждого из свободных параметров (слева направо: нижняя граница, верхняя граница и диффузия). Оси X и Y соответствуют слуховой и визуальной модальностям соответственно. Для удобства визуализации параметры, далекие от групповых значений, обрезаны и изображены пустыми кружками.
• B. То же, что и A, для модели BSU. Диаграммы рассеяния параметров показывают (слева направо): нижнюю границу, верхнюю границу и коэффициент Вебера.
• C. То же, что и A, для модели MCG. Диаграммы рассеяния параметров показывают (слева направо): среднее значение границы, стандартное отклонение границы и коэффициент Вебера.
• D. То же, что и A, для модели CG. Диаграммы рассеяния параметров показывают (слева направо): среднее значение границы, стандартное отклонение границы и коэффициент Вебера.

Таблица 3. Неидентифицируемость параметров в моделях MCG и CG.

Каждая ячейка включает количество участников (из 34), для которых конкретный параметр ({igma }_{B}, k, или оба) был оценен как меньший 0,001.

Участники используют более строгие границы и имеют меньше внутреннего шума при слуховом тайминге по сравнению с визуальным

Установив, что DDM является подходящей моделью для анализа данных отдельных участников, мы использовали ее для описания различий между условиями. Мы подогнали DDM к данным каждого участника в каждом условии отдельно (Рис. 6A) и сравнили оцененные параметры между условиями с помощью парных t-тестов.

• Нижние границы не показали значимых различий между модальностями (Maud = 0,27, SDaud = 0,06, Mvis = 0,29, SDvis = 0,09; t(33) = 0,99, p = 0,329, d = 0,17).
• Диффузия и верхние границы были сильно затронуты модальностью. Коэффициенты диффузии были значительно выше в визуальной модальности (Maud = 0,17, SDaud = 0,06, Mvis = 0,28, SDvis = 0,11; t(33) = 7,50, p < 0,001, d = 0,77). Участники устанавливали свои верхние границы на более длинных интервалах в визуальной модальности (Maud = 0,54, SDaud = 0,09, Mvis = 0,83, SDvis = 0,38; t(33) = -4,51, p < 0,001).

Как объяснено в анализе восстановления параметров, верхние границы, превышающие примерно 0,8, имеют тенденцию к переоценке. В наших данных оцененные верхние границы выше 0,8 с встречались только один раз в слуховой модальности, но 17 раз (50% участников) в визуальной. Это выявляет ограничение экспериментального дизайна. Возможно, диапазон использованных интервалов был слишком сложен для многих наших участников в визуальной модальности. Тем не менее, найденный нами эффект является надежным, несмотря на это ограничение, поскольку все участники, кроме двух, имели более высокие верхние границы в визуальной модальности.

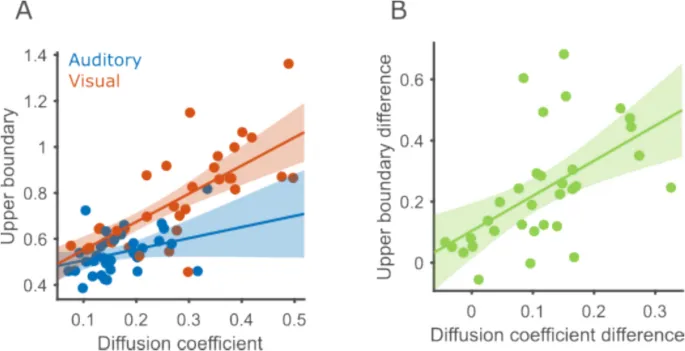
Корреляция между шумом и верхними границами

Тот факт, что как внутренний шум, так и верхняя граница значительно различались между модальностями, побудил нас исследовать, могут ли оба параметра быть изначально связаны. Если бы это было так, оба параметра должны коррелировать между участниками. Чтобы убедиться, что наш статистический анализ не был чрезмерно затронут выбросами, мы проверили верхние границы или коэффициенты диффузии, которые были на 3,5 стандартных отклонения или более от соответствующих средних. Мы исключили одного участника с верхней границей 2,6, что на 6,27 стандартных отклонения выше средней верхней границы. Мы провели линейную смешанную модель, предсказывающую верхнюю границу, используя модальность (бинарный предиктор с кодированием эффектов: -1 для аудитории и 1 для зрения) и диффузию (непрерывный предиктор) в качестве фиксированных эффектов. Перехват и наклон относительно диффузии были установлены как случайные эффекты.

Мы обнаружили, что более высокие коэффициенты диффузии коррелировали с более высокими верхними границами (β = 0,91, p < 0,001; Рис. 7A). Модальность по-прежнему предсказывала значительную вариабельность в верхних границах, даже после учета диффузии (β = -0,07, p < 0,001). Кроме того, связь между диффузией и верхней границей была сильнее в визуальной модальности, на что указывало значительное взаимодействие модальности и диффузии (β = -0,38, p = 0,011).

Важно отметить, что корреляции, наблюдаемые в эмпирических данных, больше, чем те, что наблюдались в анализе восстановления параметров. Коэффициент корреляции Пирсона между верхней границей и диффузией оценивался как 0,775. Вероятность обнаружения корреляции, равной или большей, чем эта, в симуляциях из анализа восстановления параметров, составила 0,01. Следовательно, эта корреляция выявляет истинную связь между двумя мерами, а не артефакт процедуры подгонки или спецификации модели.

Если диффузия и верхние границы связаны, другое предсказание заключается в том, что участники, продемонстрировавшие больший эффект модальности на свой коэффициент диффузии, также должны продемонстрировать больший эффект модальности на верхние границы. Поэтому мы вычислили разницу в коэффициенте диффузии между модальностями (зрение минус аудитория, поэтому мы обычно ожидаем положительные различия), а также разницу верхних границ и коррелировали эти две величины. Две разницы были значительно коррелированы (коэффициент корреляции Пирсона ρ = 0,56, p < 0,001; Рис. 7B), в соответствии с предсказанием.

В итоге, верхние границы и диффузия связаны, однако эффект модальности на верхние границы не полностью объясняется его эффектом на внутренний шум.

Рис. 7. Коэффициент диффузии и верхняя граница коррелируют.

• A. Корреляция коэффициента диффузии и верхней границы в обеих модальностях. Круги представляют данные одного участника в одной модальности (синий — слуховая, красный — визуальная). 95% доверительные интервалы регрессионных линий отмечены затененными областями.
• B. Корреляция между участниками разницы верхней границы (зрение — аудитория) и разницы коэффициента диффузии.

Психофизические функции становятся уже с увеличением опыта в задаче

Мы проанализировали данные 39 участников во втором эксперименте, изучая эффект обучения в задаче. Мы провели ANOVA с повторными измерениями по вероятности ответов «то же» с длительностью интервала (семь уровней, 0,1–0,7 с), блоком (три уровня: блоки 1–2, 3–4 и 5–6), контрастом (два уровня: 50% и 100%) и всеми взаимодействиями как внутриучастковыми факторами.

Как и ожидалось, был значительный основной эффект длительности интервала, F(2,4, 91,06) = 133,81, p < 0,001, {ta }_{p}^{2} = 0,78. Важнее, что мы обнаружили значительный основной эффект номера блока, F(1,71, 65,06) = 18,58, p < 0,001, {ta }_{p}^{2} = 0,33, а также значительное взаимодействие длительности и блока, F(4,642, 176,41) = 5,84, p < 0,001, {ta }_{p}^{2} = 0,13.

Контраст, блок по контрасту, длительность по контрасту и длительность по блоку по контрасту не были значимыми (F(1, 38) = 0,06, p = 0,815, {ta }_{p}^{2} = 0,001; F(2, 76) = 0,43, p = 0,655, {ta }_{p}^{2} = 0,011; F(4,18, 158,87) = 2,189, p = 0,07, {ta }_{p}^{2} = 0,054; F(7,84, 297,87) = 1,33, p = 0,232, {ta }_{p}^{2} = 0,034, соответственно).

Значительное взаимодействие длительности и блока означает, что участники систематически модифицировали свое поведение в ходе эксперимента. Визуальный анализ производительности участников показывает, что градиенты генерализации становились более узкими с увеличением опыта в задаче и ростом воздействия эталонных длительностей (Рис. 8A).

Чтобы изучить когнитивные основы этого изменения с обучением, мы обратимся к моделированию поведения.

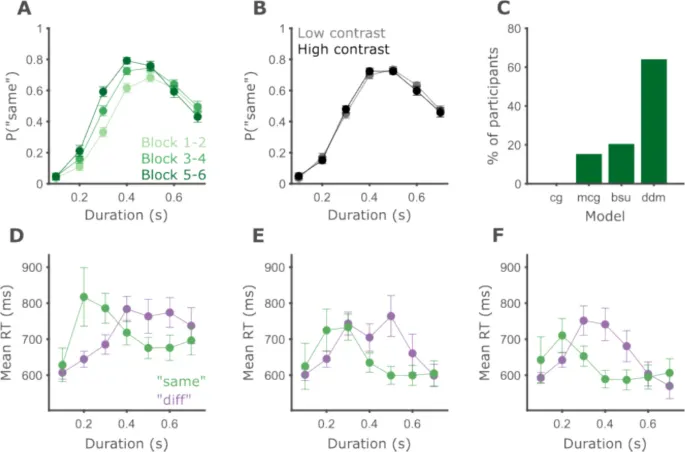
Рис. 8. Психофизическая производительность улучшается с обучением.

• A. Круги показывают среднюю вероятность маркировки интервала как «то же» по всем участникам, а полосы ошибок — внутриучастниковую стандартную ошибку среднего (SEM). Более темный цвет соответствует более поздним блокам эксперимента.
• B. То же, что и A, но испытания разделены на две группы по контрасту визуальной решетки.
• C. Процент участников (из 39) для которых каждая модель (на оси X) достигла наибольшего правдоподобия.
• D–F. Среднее время реакции для ответов «то же» (зеленый) и «другое» (пурпурный) в зависимости от длительности интервала в блоках 1–2, 3–4 и 5–6 соответственно.

Сравнение моделей и подгонка DDM

Сначала мы сравнили модели с точки зрения их способности подгонять данные. Как показано в Таблице 4, DDM обеспечила наилучшее соответствие для 64,1% участников, за ней следовали BSU с 20,5%, MCG с 15,4% и CG, которая не подошла ни одному участнику лучше всего (Рис. 8C).

Для остального анализа мы сосредоточимся на DDM.

Таблица 4. Сравнение правдоподобия моделей. Правдоподобие сравнивается между участниками по блокам. Самый левый столбец включает процент и количество участников, для которых каждая модель лучше всего подогнала их данные. Средний столбец включает суммарный логарифм правдоподобия по всем участникам как меру общего соответствия модели. Правый столбец включает отношение правдоподобия DDM к каждой модели в логарифмических единицах (log10).

Анализ параметров DDM в зависимости от блоков

Затем мы провели ANOVA с повторными измерениями по оцененным параметрам с блоком (три уровня: 1–2, 3–4 и 5–6) как внутриучастковым фактором. Мы обнаружили, что нижняя граница значительно различалась между блоками, F(2, 76) = 14,82, p < 0,001, {ta }_{p}^{2} = 0,28, смещаясь к более коротким длительностям с обучением (пост-хок тесты Тьюки-Крамера, первый против второго тертиля: p = 0,010, первый против третьего: p < 0,001, второй против третьего: p = 0,021).

Коэффициенты диффузии также значительно изменялись между блоками, F(2, 76) = 4,70, p = 0,012, {ta }_{p}^{2} = 0,11, становясь несколько меньше в ходе эксперимента. Пост-хок тест обнаружил значительное различие между первым и третьим тертилями (первый против второго тертиля: p = 0,275, первый против третьего: p = 0,017, второй против третьего: p = 0,237).

Верхние границы не показали значимых различий между блоками, F(2,76) = 2,33, p = 0,105, {ta }_{p}^{2} = 0,06. Учитывая, что верхние границы остаются достаточно близкими к краю диапазона интервалов даже в последних двух блоках эксперимента, возможно, использование более широкого диапазона интервалов также выявит систематические изменения в верхних границах (Рис. 9).

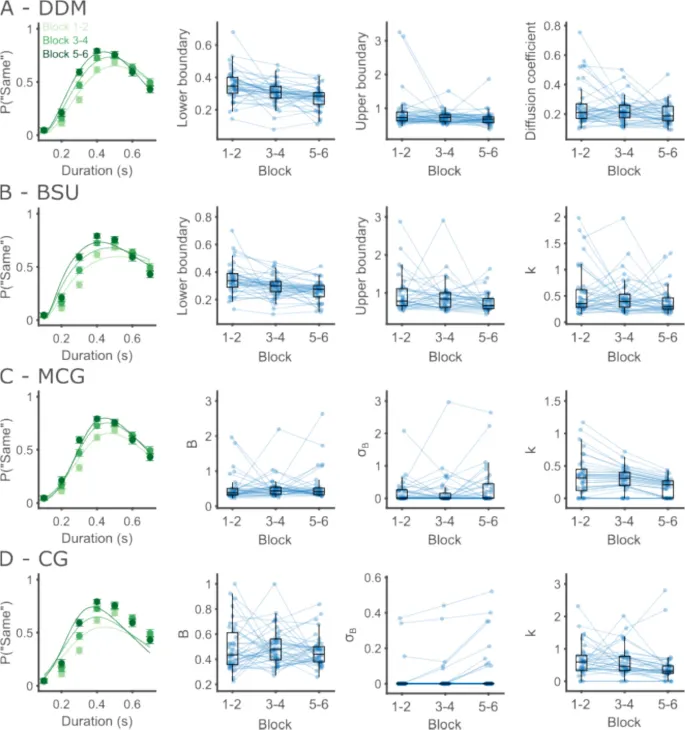
Рис. 9. Психофизическая производительность улучшается с обучением.

• A. Групповые подгонки и индивидуальные оценки параметров для каждого блока с использованием DDM. Слева — производительность и подгонка модели на групповом уровне. Круги показывают среднюю вероятность маркировки интервала как «то же» по всем участникам, а полосы ошибок — внутриучастниковую стандартную ошибку среднего (SEM). Диаграммы рассеяния показывают оцененные значения каждого из свободных параметров для данных каждого блока. Круги и соединяющие линии отмечают значения параметров между блоками для одного участника, с наложенными ящичными диаграммами. Горизонтальные линии внутри ящиков обозначают медиану группы, ящик простирается от 25-го до 75-го перцентиля, а усы простираются на 1,5 IQR от медианы.
• B. То же, что и A, но для модели BSU. Для наглядности участники с нижними границами выше 0,8, верхними границами выше 3 и коэффициентом Вебера выше 2 в любом из блоков не показаны.
• C. То же, что и A, но для модели MCG. Для наглядности участники со средним разделением границ выше 3, стандартным отклонением границ выше 3 и коэффициентом Вебера выше 1,5 в любом из блоков не показаны.
• D. То же, что и A, но для модели CG. Для наглядности участники со стандартным отклонением границ выше 0,55 и коэффициентом Вебера выше 3 в любом из блоков не показаны.

Сравнение моделей с ограничениями параметров

Мы дополняем этот анализ подходом сравнения моделей, ограничивая каждый параметр фиксированным значением для всех блоков поочередно. При упорядочивании моделей по их AIC, лучшей моделью была полная DDM, в которой все параметры могли свободно варьироваться между блоками (Таблица 5). За полной моделью следовала модель с ограниченными уровнями шума, затем модель с ограниченными верхними границами и, наконец, модель с ограниченными нижними границами.

Подходы сравнения параметров и сравнения моделей согласуются относительно явных различий в нижних границах между блоками. Они расходятся во мнении относительно того, различаются ли верхние границы между блоками. В то время как ANOVA параметров не обнаружила значимой разницы в верхних границах, AIC отдает предпочтение модели, в которой обе границы варьируются, но шум остается прежним, по сравнению с моделью, в которой шум и нижние границы варьируются, а верхние границы остаются прежними. Это может быть связано с небольшим количеством участников с очень большими различиями в их верхних границах. Хотя эти точки данных привели бы к большим оценкам внутриблочной вариабельности в ANOVA, что противоречит межблочной вариабельности, их эффекты только суммируются в используемом нами подходе сравнения моделей.

Таблица 5. Результаты сравнения моделей. Значения AIC сравниваются с полной DDM.

Корреляция между диффузией и границами

Здесь, как и при сравнении модальностей, мы обнаружили два параметра модели — коэффициент диффузии и нижняя граница — которые значительно изменились между блоками. Как и прежде, мы сначала проверили наличие выбросов в нижних границах и коэффициентах диффузии, используя критерий отсечения в 3,5 стандартных отклонения от среднего. Мы исключили одного участника, чей коэффициент диффузии в первом блоке был на 4,8 стандартных отклонения выше среднего. Затем мы использовали линейную смешанную модель для предсказания нижней границы, используя блок (категориальный предиктор с первым блоком в качестве референтного уровня), коэффициент диффузии (непрерывный предиктор) и взаимодействие коэффициента диффузии с блоком в качестве фиксированных эффектов, а также случайный перехват для каждого участника.

Как и ожидалось, нижние границы постепенно смещались к более коротким интервалам в течение блоков (второй против первого тертиля, β = -0,04, p = 0,003; третий против первого тертиля, β = -0,06, p < 0,001). Коэффициент диффузии не был значительно коррелирован с нижними границами в первом тертиле (β = 0,12, p = 0,165). Взаимодействия также не были значимыми, предполагая сходные соотношения диффузии с нижними границами в процессе обучения (второй против первого тертиля, β = -0,02, p = 0,864; третий против первого тертиля, β = 0,16, p = 0,284; Рис. 10A). Результаты смешанной модели предполагают, что обучение влияет на нижнюю границу и коэффициент диффузии независимо.

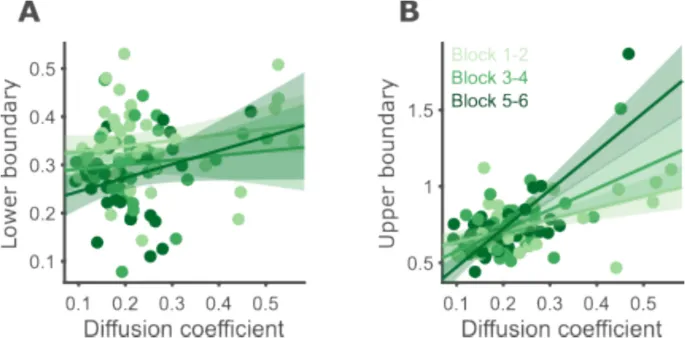
Рис. 10. Коэффициенты диффузии коррелируют с верхними, но не с нижними границами.

• A. Корреляция коэффициента диффузии и нижней границы в трех тертилях. Каждый круг представляет данные одного участника в одном тертиле (более темные цвета для более поздних тертилей). 95% доверительные интервалы регрессионных линий отмечены затененными областями.
• B. То же, что и A, но для верхних границ. Для визуализации мы использовали ту же линейную модель, что и для нижних границ.

Мы также проверили связь между верхними границами и шумом, чтобы подтвердить результаты эксперимента 1. Для этого анализа мы исключили двух участников, чьи верхние границы, и одного участника, чей коэффициент диффузии, были более чем в 3,5 SD от среднего. По всем блокам верхние границы были положительно коррелированы с диффузией, как и в эксперименте 1 (rho = 0,56, p < 0,001). Корреляция, равная или большая, наблюдалась в симуляциях восстановления параметров с вероятностью 0,04.

Границы участников близки к оптимальным при допущении равных пропорций стимулов

Анализ оптимальности границ

В обоих экспериментах мы обнаружили, что верхние границы и коэффициенты диффузии сильно коррелируют, в то время как нижние границы и диффузия — нет. Корреляция между параметрами в реальных данных была намного выше, чем наблюдалась в анализе восстановления параметров. Это предполагает, что найденная нами корреляция отражает когнитивное ограничение или стратегию.

С когнитивной точки зрения, хотя границы, вероятно, находятся под некоторым уровнем контроля, уровни шума обычно считаются чем-то, что не может быть «волевым» образом модулировано, представляя собой ограничивающий фактор производительности (Carandini, 2024; Gardner, 2019). В нашем экспериментальном дизайне не предоставляется прямого вознаграждения, обратная связь об общей точности предоставляется в конце каждого блока испытаний, и не используются временные ограничения ответа. Следовательно, мы рассматриваем оптимальность с точки зрения точности, а не скорости получения вознаграждения.

Несбалансированные вероятности стимулов

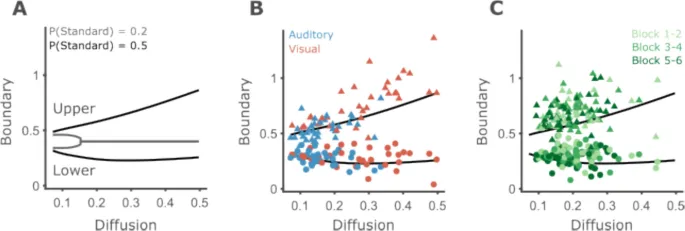
Отметим, что вероятности эталонных и нестандартных длительностей несбалансированы в обоих экспериментах. В эксперименте 1 вероятность эталонной длительности составляет 0,2, а в эксперименте 2 — 0,25. При таких условиях оптимальная стратегия с точки зрения точности — это всегда угадывать «другое» при относительно низких уровнях шума (около 0,15, Рис. 11A).

В DDM эта стратегия реализуется путем установки границ на одно и то же значение, так что вероятность того, что аккумулятор окажется между границами, равна 0. Однако многие наши участники демонстрировали уровни шума, значительно превышающие 0,15, и ни один участник не ответил «другое» во всех случаях.

Оптимальные границы при предположении равной вероятности

Возможное объяснение заключается в том, что участники предполагают, что эталонные и нестандартные длительности встречаются одинаково часто, поскольку они не могут знать истинных пропорций. Предполагая P(стандарт) = 0,5, подогнанные границы участников в целом соответствуют тому, что предсказывается для их уровня шума (Рис. 11B, C).

Исключение наблюдается для высоких верхних границ, которые, как было обнаружено, часто оказывались выше предсказанной линии. Однако, как отмечалось в разделе восстановления параметров, верхние границы, близкие или превышающие максимальную использованную длительность (0,7 с), имеют тенденцию к переоценке.

Рис. 11. Границы участников близки к оптимальным при предположении равных пропорций стимулов.

• A. Верхние и нижние границы для различных уровней шума, предполагая P(стандарт) = 0,2 (серый) или P(стандарт) = 0,5 (черный). Для уровней шума больше примерно 0,15 и P(стандарт) = 0,2, стратегия максимизации точности — всегда отвечать «другое», реализуемая путем установки обеих границ на 0,4.
• B. Наблюдаемые границы (верхние и нижние границы представлены треугольниками и кружками соответственно) против границ, максимизирующих точность (черные линии), предполагая, что P(стандарт) = 0,5. Синие символы соответствуют данным слуховой части эксперимента 1, а красные — визуальной части.
• C. То же, что и B, но для эксперимента 2. Светло-зеленый — для первых двух блоков испытаний, темно-зеленый — для последних двух блоков.

Обсуждение

Сводка моделей и результаты исследований

Считается, что разнообразный набор нейронных механизмов лежит в основе нашей способности отслеживать ход времени (Paton & Buonomano, 2018). Тем не менее, на алгоритмическом уровне многие виды поведения, связанные с таймингом, могут быть описаны как процессы ограниченного накопления (Balcı & Simen, 2024).

Фреймворк дрейфа-диффузии, который включает восприятие времени в более широкую область перцептивных решений, был применен к ряду видов поведения, связанных с таймингом. Модели DDM являются естественной основой для объяснения как бинарных ответов, так и времени реакции при временной бисекции (Balcı & Simen, 2014), а также могут объяснить паттерны ЭЭГ в этой задаче (Ofir & Landau, 2022, 2025). В данной работе мы далее расширяем фреймворк на временную генерализацию.

Предыдущие модели и предложенная DDM имеют общую базовую конструкцию психофизических моделей, а именно — сравнение переменной принятия решений с границами принятия решений, но значительно различаются в своих предположениях относительно границ и источников вариабельности:

• CG и MCG: ограничивали границы принятия решений симметрично относительно истинной эталонной длительности и предполагали, что вариабельность производительности в задаче (т. е. наклоны психофизических функций) обусловлена шумом в памяти об эталоне и границах принятия решений.
• BSU: ослабила ограничение на границы принятия решений и устранила их вариабельность от испытания к испытанию.
• DDM: мы применяем подход дрейфа-диффузии к временной генерализации. Мы определили две границы принятия решений, которые могут принимать любые значения, и коэффициент диффузии, контролирующий уровень внутреннего шума.

Сравнение восстанавливаемости моделей

Мы обнаружили, что DDM имела наиболее восстанавливаемые параметры с низкой взаимосвязью параметров. BSU достигла близкой, хотя и несколько более слабой, восстанавливаемости параметров. Анализ выявил значительные трудности в оценке параметра вариабельности принятия решений моделей MCG и CG. Мы также обнаружили, что восстанавливаемость моделей была неравномерной между моделями, при этом BSU лидировала, а DDM отставала. Увеличение количества испытаний улучшило восстанавливаемость всех моделей.

Результаты анализа восстановления параметров и моделей можно рассматривать как тесты эффективности моделей: при заданном количестве и дизайне испытаний, насколько хорошо мы можем оценить параметры модели? Такие вопросы ранее исследовались для сигмоидальных психофизических кривых (например, Wichmann & Hill, 2001), но не для немонотонных кривых, как во временной генерализации.

Превосходство DDM в подгонке данных

Кроме того, DDM превосходит все другие модели в подгонке данных отдельных участников. Это было обнаружено как для тайминга с использованием слуховых, так и визуальных стимулов. Подгонка к эмпирическим данным также прояснила компромисс между двумя параметрами шума моделей CG и MCG. Для большинства участников один из параметров был оценен в ноль, оставляя всю вариабельность для объяснения другим. Это не означает, что отсутствует вариабельность в одном из компонентов (решение или тайминг). Однако без очень больших наборов данных для отдельных участников невозможно различить оба источника вариабельности.

Преимущество DDM и BSU над CG и MCG

Лучшая производительность моделей DDM и BSU по сравнению с моделями MCG и CG, вероятно, отражает более эффективное использование доступных степеней свободы. В то время как MCG и CG используют два параметра для моделирования различных источников шума, DDM и BSU используют два параметра для подгонки смещенных психофизических кривых. Эмпирически, смещенные кривые распространены и не могут быть корректно подогнаны моделями, предполагающими симметричные границы относительно истинного эталона. С другой стороны, одного источника шума, по-видимому, достаточно для обеспечения удовлетворительной подгонки поведения в типичных экспериментах.

Различия между DDM и BSU

Различие между DDM, ведущей моделью, и BSU заключается только в том, как шум масштабируется со временем. В то время как в DDM стандартное отклонение переменной принятия решений растет с квадратным корнем времени, BSU предполагает линейный рост. Это удивительно, поскольку модели тайминга часто предполагают, что стандартное отклонение воспринимаемой длительности растет линейно со временем (Hass & Durstewitz, 2016, но см. Scott et al., 2015; Simen et al., 2011).

Модели DDM предлагают здесь уникальную перспективу: стандартное отклонение положения переменной принятия решений растет с квадратным корнем времени, в то время как стандартное отклонение времени первого прохождения растет линейно. Оригинальные модели DDM тайминга фокусировались на времени первого прохождения, а здесь мы фокусируемся на вариабельности переменной принятия решений, игнорируя момент ее пересечения границы. Будущие исследования могут более подробно изучить это различие.

Влияние модальности и обучения на параметры DDM

Наличие модели, которая может быть надежно подогнана к данным отдельных участников, позволяет статистически тестировать, как экспериментальные манипуляции влияют на когнитивные процессы, лежащие в основе поведения. Используя предложенную DDM, мы подтвердили хорошо задокументированный факт, что слуховой тайминг лучше зрительного. Мы расширяем это наблюдение, показывая, что более высокий шум тайминга в визуальных стимулах сопровождается стратегической адаптацией на уровне принятия решений. Кроме того, участники с большим шумом тайминга также имели более высокие верхние границы в обеих модальностях.

Корреляцию между шумом тайминга и верхней границей можно объяснить как стратегию максимизации точности. Это соответствует предыдущим исследованиям, которые показывают, что участники адаптируют свое поведение в соответствии с уровнем внутреннего шума (Freestone & Church, 2016; Jazayeri & Shadlen, 2010; Kononowicz et al., 2022; Maaß et al., 2021; Simen et al., 2011).

Предполагая, что шум не может быть модифицирован участником, но размещение границ — да, предполагает причинно-следственную связь: модальность влияет на шум тайминга, а шум тайминга влияет на поведенческую стратегию.

Влияние обучения на параметры DDM

Мы также использовали DDM для выявления когнитивных процессов, на которые влияет обучение в задаче, используя данные второго эксперимента по временной генерализации. На уровне сырого поведения мы обнаружили, что психофизические кривые становились более узкими и смещались в сторону более коротких интервалов с увеличением опыта в задаче и ростом воздействия эталонных длительностей. Эти изменения в DDM отражаются как снижение нижней границы принятия решений, сопровождающееся снижением коэффициента диффузии.

Мы обнаружили, что участники изначально устанавливали нижнюю границу почти на уровне истинной эталонной длительности. По мере приобретения практики в задаче участники постепенно смещали свои нижние границы к более коротким длительностям, что может отражать более точное представление эталона.

Сравнение с предыдущими исследованиями по обучению

Наши выводы контрастируют с предыдущим исследованием, которое предполагало, что верхние, но не нижние границы, снижаются с обучением (Wearden & Towse, 1994). Однако это исследование, основанное на модели MCG и ее варианте, не сравнивало статистически оценки параметров между блоками испытаний и анализировало только объединенные данные всех участников, что может быть вводить в заблуждение.

Кроме того, их объединенные поведенческие результаты (Wearden & Towse, 1994; Рис. 2) отражают в целом лучшую психофизическую производительность, чем мы наблюдаем. Например, их участники классифицировали 700-миллисекундный интервал как «то же» менее чем в 20% испытаний, в то время как в нашей выборке объединенные данные дают значение около 50%. Это можно ожидать, поскольку Уирден и Таус предоставляли обратную связь после каждого ответа, в то время как мы предоставляли обратную связь только в конце каждого блока в виде процента точных ответов.

Обратная связь по каждому испытанию, вероятно, особенно важна для более длинной части диапазона, где участники, как ожидается, будут иметь низкую уверенность в своих решениях из-за закона Вебера. Эти различия затрудняют прямое сравнение.

Предполагаемые причины смещения границ

Неясно, почему участники устанавливали свои нижние границы так близко к эталону в начале задачи. Предполагая, что участники перестают отслеживать интервал, когда приняли решение (но см. Kononowicz & Van Rijn, 2014), можно предположить, что участники начинают с высоких границ принятия решений, чтобы гарантировать накопление всей доступной информации. По мере того, как участники приобретают больше знаний о распределении интервалов в задаче, они смещают свои границы принятия решений к более коротким интервалам, что позволяет раньше готовиться к ответам и потенциально увеличивает скорость получения вознаграждения (Balci et al., 2011; Masís et al., 2023).

Аналогично, когда участникам дается инструкция отвечать как можно быстрее в задаче временной генерализации, даже до завершения интервала, вся психометрическая кривая смещается в сторону более коротких интервалов (Klapproth & Müller, 2008; Klapproth & Wearden, 2011). Критически важно, что в тех экспериментах ранний ответ прекращал интервалы, таким образом давая участникам контроль над распределением встречающихся им интервалов. В наших экспериментах участники не могли отвечать до завершения интервалов, что противоречит этому объяснению в представленном нами эксперименте.

Оптимальность границ и их независимость от шума

Мы также исследовали связь между параметрами с помощью фреймворка оптимальности. Мы обнаружили, что участники устанавливают свои границы так, как можно было бы ожидать, учитывая их уровни шума, предполагая, что они отвечают так, как если бы эталонные длительности были столь же вероятны, как и нестандартные.

Анализ оптимальности также объясняет отсутствие корреляции между уровнем шума и нижней границей. Оптимальное размещение нижней границы зависит от шума не в той же степени, что и для верхних границ. По сравнению с большой вариабельностью верхних границ для различных уровней шума, нижние границы варьируются лишь незначительно.

Неожиданный результат обучения

Интуитивно мы ожидали бы, что участники научатся на основе опыта в задаче, что эталонная длительность появляется реже, чем в 50% случаев. Это предположение означает, что в течение блоков нижние границы будут смещаться к более длинным длительностям, в то время как верхние границы будут уменьшаться к более коротким длительностям. Это контрастирует с тем, что мы обнаружили: снижение нижних границ при незначительных различиях в верхних границах.

Будущие исследования могут точно изучить, как вероятность эталона изучается с опытом в задаче.

Перспективы будущих исследований

Направления для дальнейшего изучения DDM

Заглядывая вперед, есть некоторые элементы нашей модели, которые заслуживают дополнительного внимания:

• Параметризация DDM: Во-первых, мы выбрали параметризовать нашу DDM с использованием границ принятия решений, а не внутреннего представления эталонной длительности. Однако сами границы, предположительно, только разграничивают «доверительный интервал» вокруг эталонной длительности. Альтернативная параметризация могла бы вместо этого описать внутренний эталон с симметричными границами вокруг него. Такая параметризация дала бы идентичные результаты подгонки, что и используемая нами, но могла бы быть полезной с концептуальной точки зрения.
• Стабильность границ: Например, она подчеркивает тот факт, что все четыре рассматриваемые модели предполагают, что границы принятия решений или представления эталона стабильны между испытаниями (DDM и BSU) или случайным образом варьируются от испытания к испытанию (CG и MCG). Предыдущие исследования восприятия времени, а также многие другие формы восприятия, показывают, что психофизическое поведение сильно коррелирует между испытаниями — явление, известное как серийная зависимость (serial dependence) (Cicchini et al., 2024; Hachen et al., 2021; Raviv et al., 2012; Taatgen & van Rijn, 2011; Wiener & Thompson, 2015).
• Серийная зависимость: Серийная зависимость может быть использована для проверки того, изменяются ли верхние и нижние границы принятия решений вместе или независимо между испытаниями. Если они изменяются вместе, это может поддержать параметризацию, включающую эталон явно, а не текущую параметризацию DDM, которая рассматривает границы как независимые друг от друга.

Двухэтапная модель принятия решений

Наконец, в предложенной модели мы предполагали, что границы принятия решений применяются только при завершении интервала. Переменная принятия решений может пересекать границы во время интервала, не вызывая принятия решения. Интуитивно, это предположение, вероятно, неверно, что наиболее легко увидеть на испытаниях, где интервал достаточно длинный, так что верхняя граница была достигнута до завершения интервала. В таких случаях решение «другое» может быть принято до завершения интервала, как только переменная принятия решений достигнет верхней границы.

Из этой гипотезы можно сделать два предсказания, как на поведенческом, так и на физиологическом уровне:

• Поведенческий уровень: Тот факт, что для более длинных интервалов решения «другое» могут быть приняты до завершения интервала, предсказывает более быстрое реагирование в этих случаях, поскольку моторная подготовка может начаться заранее. Мы не видим явных доказательств этого в наших данных, но наш эксперимент не был оптимизирован для сбора RT. Предыдущие исследования предоставляют некоторые доказательства того, что это так во временной генерализации (Klapproth, 2018; Klapproth & Müller, 2008; Klapproth & Wearden, 2011). Это ускорение реакции широко сообщается при временной бисекции, где решения «длинное» часто принимаются до завершения интервала (Balcı & Simen, 2014; Wiener et al., 2014; Wiener & Thompson, 2015).
• Физиологический уровень: Разделение процесса принятия решений на две стадии — до завершения интервала и после него — предполагает, что мы можем ожидать увидеть сходный паттерн нейронных сигнатур во временной генерализации и бисекции. В частности, ожидается, что потенциал, вызванный завершением интервала (offset-evoked potential), во временной генерализации будет больше для более коротких интервалов, как это происходит при бисекции (Ofir & Landau, 2022), и что моторная подготовка будет проявляться до завершения интервала (Ofir & Landau, 2025).

Насколько нам известно, только два исследования изучали потенциал, вызванный завершением интервала, во временной генерализации (Bannier et al., 2019; Özoğlu & Thomaschke, 2023). Оба исследования выявили тот же паттерн нелинейного убывающего потенциала ЭЭГ как функцию длительности интервала во временной генерализации и бисекции. Двухэтапная DDM, подобная той, что разработана для временной бисекции, будет полезным инструментом для будущих исследований, записывающих время реакции наряду с неинвазивной физиологией, для изучения временной динамики решений в задаче временной генерализации.

Заключительные выводы

Таким образом, мы предлагаем модель для временной генерализации, которая может надежно подгонять данные отдельных участников. Это позволяет нам напрямую тестировать влияние модальности стимула и обучения на когнитивные процессы, задействованные во временной генерализации. Мы надеемся, что это достижение в поведенческом анализе временной генерализации облегчит дальнейшее исследование этой задачи как на поведенческом уровне, так и в качестве основы для соотнесения нейронной активности с лежащими в основе когнитивными процессами.